Дифференциальные уравнения первого порядка

Дифференциальные уравнения 1-го порядка.

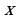Обыкновенным дифференциальным уравнением называется уравнение, содержащее независимую переменную , искомую функцию 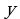и ее производные :

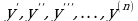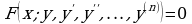(1)

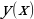Решением дифференциального уравнения n-го порядка называется функция , имеющая на некотором интервале 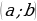производные 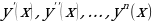и удовлетворяющая этому уравнению. Процесс решения дифференциального уравнения называется интегрированием. Таким образом, каждому дифференциальному уравнению соответствует, как правило бесконечная совокупность его решений.

Всякое, отдельно взятое решение дифференциального уравнения, называется его частным решением.

Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши.

Порядок наивысшей производной, входящей в уравнение, называется порядком дифференциального уравнения.

Дифференциальные уравнения с разделяющимися переменными.

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида

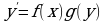(1) Заменим 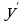на

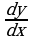
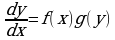(1) Разделим переменные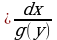

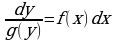(2) Проинтегрируем обе части равенства

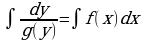(3) Найдем первообразные

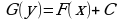(4) Общий интеграл уравнения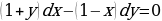

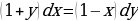
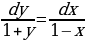
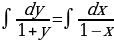
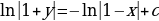
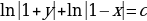
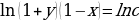
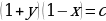
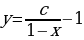При решении дифференциальных уравнений с разделяющимися переменными (1) можно руководствоваться следующим алгоритмом:

1. разделить переменные (с учетом условий, когда это возможно);

2. интегрируя почленно полученное уравнение с разделенными переменными (2), найти его общий интеграл (4);

3. выяснить, имеет ли уравнение (1) решения, не получающиеся из общего интеграла (4);

4. найти частный интеграл (или решение), удовлетворяющий начальным условиям (если это требуется).

Пример 1. Найти общее решение уравнения:

Решение.

Разделим переменные:

Проинтегрируем обе части уравнения:

Вычислим интегралы:

Выразим y: - искомое общее решение.

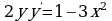Пример 2. Найти частное решение уравнения , если 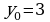при

Решение. Это уравнение с разделяющимися переменными, тогда

Подставим начальные значения в полученное равенство, найдем С:

Следовательно, искомый частный интеграл будет

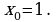
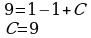
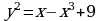или