ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПРОФЕССИОНАЛЬНЫЙ ЛИЦЕЙ № 4»
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
ТЕМА: «ДИФФЕРЕНЦИРОВАННЫЙ ПОДХОД К УЧАЩИМСЯ ПРИ ОБУЧЕНИИ МАТЕМАТИКЕ.».
(Работа со слабоуспевающими обучающимися)
Автор: преподаватель
М.И.Хугаева
г. Владикавказ, 2019 г.
Организовать ликвидацию пробелов можно, если предусмотреть ряд мер:
1) определение уровня знаний и умений учащегося математики 5-9 классов;
2) определение типичных для предмета и для конкретной учебной группы пробелов в знаниях и умениях;
3) анализ содержания учебного материала за 9-летнюю школу и выявления базовых знаний и умений по предмету, необходимых для успешного совладения математикой в дальнейшем, а также для успешного овладения спец. дисциплинами;
4) использования для воспитания пробелов не отдельных приемов, средств и форм работы, а разнообразных их сочетаний;
5) строгий учет ликвидируемых пробелов;
6) создание уверенности у слабоуспевающих обучающихся в своих силах.
В лицее уделяется особое внимание выявлению пробелов в знаниях, обучающихся и работе по их ликвидации. Всем ясно, что без повторения на 1 курсе необходимого минимума учебного материала по алгебре и геометрии приступать к дальнейшему изучения нерационально. Основные понятия, подлежащие повторению по алгебре это множество и операции над ними, выражения и преобразования их, уравнения и неравенство, функции. По геометрии - аксиомы планиметрии, параллельность и перпендикулярность, зависимость между элементами треугольника, многоугольника и т.д.
Как показывает опыт, количество часов, отведенных на повторение согласно программе, далеко недостаточно. Поэтому целесообразно повторение в начале учебного года организовать по принципу обзора и систематизации фактов, понятий и зависимостей, отмеченных выше. После обзора проводятся вводные проверочные контрольные работы по химии, физике, математике и русскому языку (диктант). Задачи и упражнения очень просты.
Контрольные работы подробно анализируются педагогами, проводившими их, и доводятся до сведения всего инженерно-педагогического коллектива на инструктивном совещании.
Результаты этих работ позволяют выявить основные пробелы в знаниях обучающихся, наметить меры по их ликвидации, показывают, в каком объёме следует повторять необходимый материал.
Одной из основных форм для ликвидации пробелов в знаниях учащихся, служит организация дополнительных занятий и консультаций.
В зависимости от глубины пробелов планируется продолжительность дополнительных занятий. Сроки могут быть разными.
Для учета изменений в знаниях, обучающихся периодически проводятся тестирования, контрольные и самостоятельные работы. Они позволяют опять выявить темы, оставшиеся непонятными и спланировать дальнейшую работу.
В ходе проведения дополнительных занятий особое место отводится повторению периодического материала, ибо нет практики без теории. Для проверки теоретических знаний неуспевающих учащихся привлекаются сильные учащиеся. Они могут принимать зачеты у слабоуспевающих учащихся по отдельным вопросам или просто заслушивать устные ответы учеников, которые по разным причинам испытывают сильное волнение, смущение при ответе преподавателю.
Нельзя конечно думать, что описанной выше работы достаточно, чтобы ликвидировать все пробелы в знаниях обучающихся. В дальнейшем слабоуспевающим со школы учащимся будет легко усваивать новый материал.
Решения проблемы успешного обучения учащихся развития их познавательной активности опираются на дифференцированный подход к обучению как средству формирования положительного отношения к учебе, познавательных способностей.
Каждый педагог должен понимать, что без индивидуализации не может быть развивающего обучения. Одним из принципов развивающего обучения является специальное формирование обобщенных приемов умственной деятельности, которые делятся на две группы - алгоритмического и эвристического типа.
Различные виды индивидуализации обучения могут создать необходимые условия для развития у обучающихся этих приемов умственной деятельности. В практике обучения математике чаще всего дифференцируют по степени трудности самостоятельные работы и дополнительные задания. Другими словами, учитывается специфика умственной деятельности обучающихся.
При введении нового материала одни обучающиеся усваивают его сразу и легко оперируют новыми понятиями, другие достигают высшего уровня усвоения лишь после длительной дополнительной работы. Имеются и такие, которые к моменту перехода к новому материалу не успевают овладеть тем, что изучалось раньше.
Обучающиеся, медленно усваивающие знания, проходят в основном те же этапы в процессе обучения, что и их товарищи, но для этого им требуется значительно больше времени. Слабо успевающие обучающиеся медленно воспринимают новый материал, у них с трудом протекает процесс формирования понятий и установления связей между ними. Если не учитывать индивидуальные особенности этой категории ребят, осуществлять дифференцированную работу с ними на уроках, не оказывать необходимой помощи, то уже на уроке у них будет накапливаться, отставание в усвоении учебного материала. Интерес к учению может ослабеть, что приведет к снижению успеваемости.
Нельзя признать плодотворной практику, когда всем обучающиеся без учета их определяющихся склонностей предлагают одно и то же задание. В этом случае преподаватель пытается оценить способности обучающихся одним критерием. Однако необходимо изыскивать пути и способы одновременной работы со всей группой и с отдельными обучающимися.
Успех в учении - основной фактор, способствующий устойчивому интересу к учебному предмету. В педагогической литературе отмечается: обучающиеся любят то, что понимают, в чем добиваются успеха, что умеют делать. Следовательно, нужно выявить причины нежелания учиться, составить перечень всех пробелов в знаниях, наметить сроки их ликвидации, прикрепить к слабым обучающимся сильных в качестве консультантов, при возможности раз в неделю справляться о выполнении задания, давать советы, как успешнее сделать его.
При оценке целесообразно учитывать лишь те ошибки и пробелы, которые появились при изучении нового материала. Это помогает обучающимся подтянуться, поверить в свои силы, воспитывает у него потребность заниматься регулярно.
Учитывая контингент обучающихся, хочется подробнее остановиться на работе со слабоуспевающими. Именно эти обучающиеся особенно нуждаются в оценивании своей работы. Особенно в первом этапе работы с отстающими, оценка должна быть направлена на поддержку, укрепление положительных мотивов учения. В связи с этим к оцениванию предъявляются особые требования, которые находят свое выражение в следующих приемах:
1) создание ситуаций успеха у обучающихся путем поощрения за проявленную инициативу, находчивость, смелость мысли, активность, найденную ошибку, правильное повторение вывода и т.д.;
2) выставление дифференцированных отметок за отдельные умения, знание отдельных вопросов темы ( формулировки законов, правил, написание формул, уравнений и пр.) с тенденций на завышение (на первых порах).Говоря об оценивании и контроле учебной работы слабоуспевающих обучающихся , нельзя не отметить, что любое оценочное воздействие на ученика, в особенности оценка его знаний, может оказать влияние на его деятельность только в том случае, если он понимает критерии, на которых она основана и внутренне с ними согласен.
Установлено, что для этого необходимо включать ребят в оценочный процесс, предлагая ему критически анализировать и оценивать свою работу на основе определенных требований. Опыт работы подтверждает эффективность данного приема в работе с отстающими обучающимися. Преподаватели сообщают им о требованиях к устным ответам, к оформлению письменных отчетов и выполнении самостоятельных работ различных видов и пр., демонстрируют эти требования при комментировании и оценивании действий ребят, затем привлекают хорошо успевающих обучающихся к комментированию ответов своих товарищей по группе, взаимной проверке письменных работ, приему зачетов одними обучающимися у других. Преподаватели нередко наблюдают на своих уроках, как слабоуспевающие обучающиеся стремятся остаться незамеченными в те моменты, когда педагог обращается к группе с вопросами и ждет, кто поднимет руку и ответит. Будучи неуверенными в себе, они не решаются поднять руку даже тогда, когда домашние задания ими выполнены, они знают материал и им есть что сказать. Чаще всего отстающие обучающиеся в процессе коллективного обсуждения каких-либо вопросов безучастны на уроках, и попытки преподавателей привлечь их к ответам на возникающие вопросы, к высказыванию мнений далеко не всегда успешны. Причины этого кроются в свойственном им ощущении безнадежности, предчувствии безуспешности, попытки показать себя знающим и умеющим. Учитывая эту особенность эмоционального состояния слабоуспевающих ребят на уроке, применяются специальные приемы, с помощью которых выводят их из пассивного состояния, помогают им занять в группе активную позицию и тем самым более престижное положение среди своих товарищей.
Например,
1) вести на доске записи, сопровождающие объяснение преподавателей;
2) помочь преподавателю в использовании на уроке наглядных и технических средств, в проведении демонстрационного эксперимента и т.п.;
3) подготовить к очередному уроку технические средства, начертить плакат-схему, написать карточку-задание и т.п.;
4) смастерить макет, модель и др.
Предложение этих и подобных поручений слабоуспевающим обучающимся имеет смысл и пользу в том случае, если усилия обучающихся не пропадают даром и ребята видят, что старались не напрасно, что пре подаватель использует на уроках сделанные их руками плакаты, модели. Огромная роль в осуществлении индивидуального подхода к слабоуспевающим принадлежит педагогическому такту. Какие бы приемы преподаватель не использовал на уроке, они могут оказаться безуспешными, если при этом отстающие ребята не чувствуют веры преподавателя в то, что они способны овладеть учебной программой, если преподаватель не выражает словом, тоном, взглядом и примером уважения к ним, искреннего стремления помочь в преодолении трудностей. Отношение к обучающимся средних профтехучилищ должно быть проникнуто особым уважением и заботой о том, чтобы они не только успешно овладели своей будущей специальностью, но и получили хорошую общеобразовательную подготовку, чтобы формирование личности квалифицированного рабочего отвечало современным требованиям и перспективам социального развития.
Немаловажным является работа с сильными обучающимися. Их в группе бывает гораздо меньше. Иногда разрыв в знаниях, способностях, умениях бывает очень велик. Преподаватель должен помнить, что, если организовать работу со ориентацией только на средних и слабоуспевающих обучающихся, у остальных пропадет интерес к предмету, они перестанут стремиться к более глубокому познанию учебного материала. С этой целью на уроках им предлагаются всевозможные карточки с задачами повышенной трудности.
Индивидуальный подход в обучении включает в себя использование дифференцируемых домашних заданий. Известно, что одни на уроке успевают понять и суть изучаемого вопроса и выполнить различные задания на применение полученных знаний, другие едва справляются с самыми элементарными заданиями. Поэтому домашнее задание для одних становится слишком легким, а для других трудным. Исходя из этого, успевающим обучающимся для работы дома предлагаются более трудные задания, а слабоуспевающим указывается, какие разделы учебникам нужно повторить, на что следует обратить внимание.
Обучающиеся должны помнить, что на дом задается то, что необходимо для полного усвоения, изучаемого материала, прочного формирования умений и навыков, что домашняя работа не формальное дополнение к урокам, а необходимое условие успешного учения.
Дифференцированный подход к обучению предусматривает использование соответствующих дидактических материалов: специальных обучающих таблиц, плакатов и схем для самоконтроля, карточек-заданий, определяющих условие предполагаемого задания; карточек с текстами получаемой информации сопровождаемой необходимыми разъяснениями, чертежами; карточек, в которых показаны образцы того, как следует вести записи решения; карточек-инструкций, в которых даются указания к выполнению задания и др.
Как же наиболее рационально организовать дифференцированную работу обучающихся на уроках и при выполнении домашних заданий. Кандидат педагогических наук В.К.Буряк в книге для учителя "Самостоятельная работа учащихся" рассматривает систему дифференцированных заданий, которая помогает правильно организовать изучение той или иной темы:
1) задания по степени трудности - облегченной, средней и повышенной (выбор варианта предоставляется учащемуся), сигнальные карточки;
2) общие для всей группы задания с предложением системы дополнительных заданий все возрастающей степени трудности;
3) индивидуальные дифференцированные задания;
4) групповые дифференцированные задания с учетом различной подготовки обучающихся (вариант определяет преподаватель);
5) равноценные двухвариантные задания по рядам с приложением к каждому варианту системы дополнительных заданий все возрастающей трудности;
6) общие практические задания с указанием минимального и максимального количества заданий или примеров для обязательного выполнения;
7) индивидуально-групповые задания различной степени трудности по уже решенным задачам или примерам;
8) индивидуально-групповые задания, предлагаемые в виде запрограммированных карточек.
Опыт работы показывает, что дифференциация заданий особенно важна при закреплении нового материала, когда происходит его усвоение, а также повторении пройденного. Но преподаватель должен всегда помнить, что при подготовке к проверке знаний, обучающихся важно выделить контролируемые результаты обучения - систему фактов, обязательных для усвоения всеми обучающимися.
Ниже будут рассмотрены различные виды дидактических материалов для осуществления дифференцированного подхода к обучающимся при обучении математике, применяемые в работе.
ПРИМЕРЫ
Рассматривая раздел "Тригонометрические функции числового аргумента, можно использовать следующие виды карточек:
Карточка-инструкция
Вычислить сos(α+β), если известно, что sinα=sinβ=5/13 0
План решения и некоторые указания:
1. В формуле сos(α+β) = выделить функции, значения которых неизвестны.
2. Значения этих функций находятся из соотношения
Sin2 х+cos2 x=1,
откуда
cosx=± 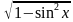
3. При определении знака функции следует учесть ее знак в данной четверти 0
т.е., угол α в I четверти, π/2 т.е., угол α во II четверти.
4. Подставить соответствующие значения в формулу
сos(α+β)=cosαcosβ – sinαsinβ и произвести вычисления.
Карточка-инструкция
по теме "Решение логарифмических уравнений".
Решите уравнение: log3(x2–6x+17)=2.
Указание:
1). Найдите область определения. Для этого надо решить неравенство:
X2– 6x+170;
2). Замените 2 на log39;
3). Решите уравнение: log3(x2–6x+17) =log39;
4). Проверьте, все ли получившиеся значения переменной входят в область определения;
5). Запишите ответ.
Более “сильным” обучающимся можно предложить решить это уравнение ещё и другим способом (используя определение логарифма).
Карточка – образец
по теме: «Применение производной к исследованию функции».
1. Если f '(x) 0 в каждой точке интервала (a;b), то функция f(x) возрастает на этом интервале.
Если f '(x) в каждой точке интервала (a;b), то функция f(x) убывает на этом интервале.
2. Найдите промежутки возрастания и убывание функции
f(x)=2x2 – 8x + 3.
Решение:
1. Данная функция определена на множестве R:
2. f '(x)= (2x2 – 8x + 3)' = 4x – 8;
3. f '(x)0, если 4х – 8 0 4х 8 х 2.
Функция возрастает на интервале (2; + ∞);
4. f '(x) 4х х
Функция убывает на промежутке (-∞; 2)
5. Так как функция f '(x)=2x2 – 8x + 3 непрерывна в точке х0 =2,
то f(x) возрастает на промежутке [2; +∞); и убывает на промежутке (-∞; 2].
Ответ: функция f(x) возрастает на промежутке [2; +∞);
функция f(x) убывает на промежутке (-∞; 2].
2. Самостоятельно определить промежутки возрастания и убывания функции
f(x)=7x2 +3x -12.
Карточка с цветовыми сигналами.
По теме: "Углы между прямыми и плоскостями".
Карточки используются при написании контрольной работы.
В ариант_1
ариант_1

1. Из точки, отстоящей от плоскости на расстоянии 10см,
проведены две наклонные, образующие с плоскостью углы 45° и
60°. Угол между проекциями наклонных прямой. Найдите
расстояние между основаниями наклонных.
2. Два равнобедренных треугольника ABC и АВD имеют общее основание АВ. Найдите угол между плоскостями этих треугольников, если АВ=16, АС=17, AD=V81, а расстояние между их вершинами С и D равно 13.
 данные
данные
 неизвестное
неизвестное
Чаще всего обучающиеся испытывает трудности при решении задач потому, что не знают, с чего начать, не знают общего метода решения уравнений и неравенств конкретного типа. Алгоритмические предписания содержат инструкцию по решению таких заданий, поэтому их можно широко использовать для выработки у обучающихся умений и навыков на уроке обязательных результатов обучения. Так, разобрав вместе с обучающимися на конкретном примере общую схему решения уравнений данного типа, с помощью компьютера проецируются на экран соответствующие шаги алгоритмического предписания, и предлагается обучающимся решить аналогичный пример. Далее, слабые обучающиеся, видя образец, выполняют задание. Это способствует выработке необходимых умений.
Как известно, большое место в методике отведено осуществлению дифференцированного подхода к обучению обучающихся. С этой целью алгоритмические предписания можно использовать как нельзя лучше. Слабым учащимся даются карточки-образцы и аналогичные примеры; более подготовленным после ознакомления с алгоритмом можно предложить карточки только с заданием; сильным - задание на составление алгоритмических предписаний, их дополнение и усовершенствование.
Приведем примеры наиболее эффективного использования алгоритмических предписаний в процессе обучения математике в 10-11классах.
| №№ шагов | Алгоритмическое предписание решения уравнения af(x) = a4(x) (1) | Решить уравнение 32x-1 x 9x-2 = 27 (2) |
| 1. | Приведите уравнение к виду af(x) = a4(x) (1) | 32x-1 x 32(x-2) = 27 32x-1+2(x-2) = 33 |
| 2 | Т.к. в уравнении (1) степени равны, основания степеней равны, то в области действительных чисел показатели степеней также равны между собой. Приравняйте показатели степеней (2) | 2x – 1 + 2(x-1) = 3 2x – 1 + 2x-1 = 3 4x = 8; x = 2 |
| 3. | Запишите ответ | 2 |
Исследование функции при помощи производной
| №№ шагов | Алгоритмические предписания | Построить график функции у = -3x2 + 4x-1 |
| 1. | Найдите область определения функции D(y) | D(y)= R |
| 2 | Найдите производную функции y' | y'= (-3x2 + 4x-1)' = -6x + 4 |
| 3. | Найдите критические точки функции. | -6x + 4= 0; -6x = - 4; x= 2/3. |
| 4. | Определите промежутки монотонности (возрастания и убывания) функции | Заданная функция возрастает на промежутке, где y' 0: -6x + 40, x Заданная функция возрастает на промежутке, где y' -6x + 4x 2/3, (2/3; + ∞) |
| 5. | Найдите экстремумы функции (максимум, минимум) | Так как слева от точки x= 2/3 функция возрастает, а справа убывает, то в точке x= 2/3 она достигает максимума: ymax=y(2/3) = -3x(2/3)2+4x2/3-1=1/3 |
| 6. | Установите чётность, нечётность, периодичность функции | Функция чётная, т.к. Прямая х=2/3 – ось симметрии графика. |
| 7. | Определите точки пересечения графика с осями координат. | -3x2 + 4x-1=0, -3x2 + 4x+1=0. х1= 1/3, х2= 1, х=0, y=-1 |
| 8. | Результаты исследования сведите в таблицу. | | x | (-∞;2/3) | 2/3 | (2/3; + ∞) | | y' | + | 0 | - | | y | 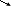
| 1/3 | 
|
|
| 9. | Постройте график функции. |

|
Для оказания помощи «слабым» обучающимся в решении задачи 8 (§14) которая может быть задана на дом, им даются карточки, содержащие план решения этой задачи:
Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости.
План решения:
1. Возьмите прямую b и точку A, не лежащую на ней.
2. Через точку A проведите прямую a, пересекающую прямую b.
Обозначьте точку пересечения прямых a и b.
3. Примените теорему 14.1 - получите плоскости a.
4. Докажите, что прямая a лежит в полученной плоскости α.
5. Сделайте общий вывод.
К этой задаче можно предложить и другое решение:
1. Возьмите прямую a и точку B, не лежащую не ней.
2. Возьмите на прямой a точку A и проведите прямую AB.
Сделайте ссылки на аксиомы, по которым возможно произвести это построение.
3. Возьмите на прямой a точку C, отличную от точки A, и проведите прямую cb. Что можно сказать о взаимном расположении прямых Ab и a, bС и a, Ab и cB?
4. Сколько плоскостей можно провести через каждую из пар прямых AB и a? BC и a? AB и cb?
5. Рассмотрите, сколько имеется точек, не лежащих на одной прямой. Сделаете вывод.
Карточка к теореме "Признак перпендикулярности прямой и плоскости" (с.191, рис.2.32 учебного пособия А.В. Погорелова.
1.Укажите точку пересечения прямой a с плоскостью α.
2.Перпендикулярность каких прямых нам дана?
3.Зачем через точку пересечения прямой a с плоскостью α проводится третья прямая x?
4. Какое еще дополнительное построение производится?
5. Почему Δ A1 C A2 равнобедренный? Запишите равенство его соответствующих сторон.
6. Почему Δ A1 C A2 равнобедренный? Запишите равенство его соответствующих сторон.
7. Почему Δ A1 BC = Δ A2 BC? Запишите равенство, тех углов этих треугольников, которые входят в Δ A1BX и Δ A2 BX.
8. Почему Δ A1BX = Δ A2BX ? Запишите равенство тех сторон этих треугольников, которые входят в Δ A1X A2.
9. Какого вида Δ A1X A2? Чем является в этом треугольнике отрезок XA?
10. Почему из перпендикулярности прямых a и x следует перпендикулярность прямой a и плоскости α?
Таким образом при умелом и рациональном использовании различного вида дифференцированных заданий на разных этапах урока можно добиться успешного овладения программного материала всеми учащимися, повысить прочность усвоения ими знаний и умений, научить осознанно использовать приобретенные знания, максимально обеспечить продуктивную работу всех учащихся, мобилизовать их способности, полнее развить склонности и интересы.





 ариант_1
ариант_1
 данные
данные неизвестное
неизвестное