Муниципальное бюджетное общеобразовательное учреждение
Новонукутская средняя общеобразовательная школа
Тема
Длина окружности
6 класс
Учитель математики
первой квалификационной категории
Леонова Ксения Владимировна
Новонукутский, 2020
Цели урока:
Образовательные:
- изучить формулу длины окружности;
- показать применение её при решении задач;
- познакомиться с числом π;
-прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.
Развивающие:
- развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
-развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы;
-формировать умения чётко и ясно излагать свои мысли;
-развивать пространственное воображение учащихся.
Воспитательные:
- прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности;
- воспитывать умение работать с имеющейся информацией в необычной ситуации;
- воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире;
-развивать интерес к математике путем создания ситуации успеха.
Тип урока:
Урок изучения и первичного закрепления новых знаний
Оборудование:
проектор,
компьютер,
карточки с заданиями (приложение 1),
презентация-cопровождение в Power Point (приложение 2).
Ход урока
Организационный момент.
Здравствуйте, ребята! Меня зовут Леонова Ксения Владимировна.
Кто отсутствует на уроке?
Актуализация знаний.
ЗАДАНИЕ №1
Чтобы узнать тему нашего урока мы должны разгадать кодовое слово.
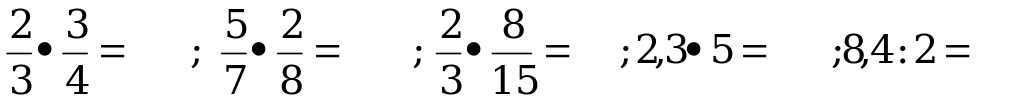
Расшифровка
Первое слово вы угадали- ДЛИНА. А второе мы узнаем из стихотворения.
Вроде круг, но дело в том
Что иначе мы зовем
Нарисованный кружок.
В чем секрет? Скажи дружок!
Это странная наружность
Называется ОКРУЖНОСТЬ!
- Какие предметы имеют форму окружности? (Слайд )
-Что общего у этих предметов?
-Чем отличаются эти предметы?
Сейчас давайте посмотрим на экран и узнаем какие основные элементы существуют у окружности.
Чертим вместе в тетрадях.
-Тема сегодняшнего урока длина окружности. Как вы думаете, что это такое?
А теперь давайте попробуем решить такую задачу.
Задача: Найдите, какой длины бордюр потребуется для ограждения клумбы, имеющей форму круга с радиусом, равным 1,5 м.
-Как вы думаете, что мы должны знать, чтобы разбить клумбу? (Длину окружности)
- Вспомните единицы измерения длины
- С помощью какого инструмента можно измерять длину, например длину отрезка?
- А можно ли измерять линейкой длину окружности?
- У каждой окружности есть своя длина. Как вы думаете, как ее измерить?
Показываю, с помощью нитки и линейки.
Вывод формулы длины окружности
Давайте выполним с вами следующую практическую работу.
ЗАДАНИЕ №2
Найдите отношение длины окружности к ее диаметру.
Указание:
1.Перед вами стоят игрушки. Что у них в виде окружности?
2.Обведите окружность нитью, измерьте её длину и запишите ответ в тетрадь
3.С помощью линейки измерьте диаметр окружности и запишите его значение в тетрадь
4. Вычислите отношение длины окружности к ее диаметру с точностью до тысячных и округлите полученное число до сотых;(повторить правило округление десятичных дробей)
5.Какой вывод можно сделать?
Какими бы различными ни были окружности, отношения их длин к диаметрам будут постоянно одинаковыми. Длина окружности больше диаметра приблизительно в 3 раза.
Мы получили число 3,14, его называют числом Пи.
Историческая справка.( о числе пи)
Число П – бесконечная десятичная дробь.
Обозначение числа происходит от первой буквы греческого слова периферия, что означает "окружность".
На ранних ступенях человеческого развития пользовались неточным числом p. Оно было равно 3. Египетские и римские математики установили отношение длины окружности к диаметру не строгим геометрическим расчётом, как позднейшие математики, а нашли его просто из опыта.
В 3в. до н.э. Архимед без измерений одними рассуждениями вычислил точное значение числа p=22/7
Общепринятым это обозначение стало, после одной из работ Эйлера, великого математика обозначали буквой П (пи).
С помощью компьютера число П находят с точностью до миллиона знаков, но это представляет технический интерес, а не научный. Для обычных вычислений с числом p вполне достаточно запомнить два знака после запятой .
Чтобы запомнить было легче, существует небольшое четверостишье:
Нужно только постараться
И запомнить все как есть
Три, четырнадцать, пятнадцать
Девяносто два и шесть.
Вернемся к нашей проблеме нахождения длины бордюра. А сможете ли с помощью всё той же нитки найти длину любой окружности.
Конечно же нет, но зная, что с/d = П, выразим длину окружности С=Пd .
Итак- Длина окружности равна произведению диаметра на число П.
А так как d=2r, то С =2Пr
-Запишите формулы в тетрадь.
Решим нашу задачу (лестница для решения)
С =2Пr, что нам известно? Радиус равен 1,5 метра. Подставим данное значение в формулу
C=2πr=2*3,14*1,5=3*3,14=9,42(м)
Физминутка
Рисуй глазами треугольник
Рисуй глазами треугольник
Теперь его переверни вершиной вниз
И вновь глазами ты по периметру веди.
Рисуй восьмерку вертикально,
Ты головою не крути,
А лишь глазами осторожно
Ты вдоль по линиям води.
И на бочок ее клади.
Теперь следи горизонтально,
И в центре ты остановись,
Зажмурься крепко не ленись.
РЕШЕНИЕ ЗАДАЧ
ЗАДАЧА 1.
Найдите длину окружности, если длина его диаметра 5 см.
РЕШЕНИЕ: С = π · d = 3,1 · 5 = 15,7 см.
ОТВЕТ: С = 15,7 см.
ЗАДАЧА 2.
Найдите диаметр окружности, длина которой равна 6,28 м.
РЕШЕНИЕ: С = π · d = d = С : π = 6,28 : 3,14 = 2 м.
ОТВЕТ: d = 2 м.
ЗАДАЧА 3.
Найдите радиус окружности, длина которой 18,84 дм.
РЕШЕНИЕ: С = 2 · π · r = d= С: π = d=18,84: 3,14 =d=6 дм
r = d:2 = r=6:2=3 дм
ОТВЕТ: r = 3 дм.
Самостоятельная работа (ТЕСТ)
ТЕСТ
| № | ВОПРОС | ОТВЕТ |
| 1 | Отрезок, соединяющий две точки окружности, проходящий через центр окружности | А) хорда, Б) Диаметр В) радиус |
| 2 | Число π равно | А) 3, 15 Б)3,14 В)6,28 |
| 3 | Формула длины окружности | А) С=πr Б) С=πd В) C=2πd Г) C=2r |
| 4 | Чему равен диаметр окружности, радиус которой 3,2 см? | А) 1,9 Б) 6,6 В) 7,6 Г) 6,4
|
| 5 | Диаметр равен половине радиуса | А) да Б) нет |
|
| ОЦЕНКА | ______ |
2). Правильный ответ обведите кружочком.
3). Посчитайте число правильных ответов и поставьте себе оценку
(1 правильный ответ = 1 баллу).
Домашнее задание.
№649; №653
Итоги урока (1 мин.)
– Мы на славу потрудились. Пришло время подвести итоги нашего урока.
– Что вы нового сегодня повторили? Узнали? Закрепили?
-Какие формулы мы вывели самостоятельно?
– Чему научились?
-Пригодится ли нам эта тема в жизни? В каких областях мы можем использовать длину окружности?
(Применять эти формулы для решения задач).
Самоанализ урока учителя математики Леоновой К.В.
Тема «Длина окружности». 6 класс.
Тип урока: Урок изучения и первичного закрепления новых знаний
Данный урок проводился по плану в соответствии с тематическим планированием. На урок были поставлены следующие цели:
Образовательные:
- изучить формулу длины окружности;
- показать применение её при решении задач;
- познакомиться с числом π;
-прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности.
Развивающие:
- развивать познавательный интерес учащихся в процессе ознакомления с историческим материалом;
-развивать творческую и мыслительную деятельность учащихся, их интеллектуальные качества: способность к «видению» проблемы;
-формировать умения чётко и ясно излагать свои мысли;
-развивать пространственное воображение учащихся.
Воспитательные:
- прививать учащимся навык самостоятельности в работе, учить трудолюбию, аккуратности;
- воспитывать умение работать с имеющейся информацией в необычной ситуации;
- воспитывать уважение к математике, умение видеть математические задачи в окружающем нас мире;
Этот урок проводится в классе, где большинство имеют средние знания, умения, навыки, хотя, конечно, есть и такие, у которых отсутствует познавательный интерес, у 1-го человека в классе – большие пробелы в фактических знаниях и умениях.
Исходя из особенностей класса и темы урока, думаю обучающий аспект можно сформулировать широко: контроль уровня усвоения знаний и умений нахождения длины окружности по формуле, вычислительных навыков; формирование умения и навыков выводить формулу через практическую работу, т.к. тема во многом знакома учащимся (понятие окружности, его элементов, зависимость диаметра через радиус) и класс подготовлен к сопоставлению, анализу
Образовательный аспект позволяет поставить такие развивающие цели: развитие умений выделять главное, существенное в изучаемом материале; формирование умений сравнивать, обобщать факты и понятия; развитие у учащихся самостоятельности в мышлении и учебной деятельности; развитие у учащихся познавательного интереса.
Этапы урока:
Организационный момент
Актуализация знаний
Вывод формулы длины окружности
Физминутка
Решение задач с использованием формул
Самостоятельная работа
Домашнее задание
Подведение итогов
При подготовке урока я ставила перед собой следующие задачи:
- повторить и закрепить знания учащихся об окружности;
- обеспечить усвоение учащимися формул для вычисления длины окружности;
- отработать применение данных формул при решении задач;
- расширить кругозор учащихся сведениями из истории математики;
- развивать навыки самостоятельной работы и работы в парах;
- воспитывать уважительное отношение друг к другу.
Для достижения поставленных целей я использовала следующие приемы и методы:
- словесные (речь учителя, рассказ об истории возникновения числа π);
- наглядные (мультимедийная презентация всех этапов урока);
- письменных и устных упражнений и самостоятельных работ- методы устного и письменного контроля и самоконтроля.
В ходе урока были использованы различные формы работы учащихся:
- коллективная;
- работа в парах;
- индивидуальная.
С целью активизации работы на уроке были использованы различные виды проверок: самопроверка со слайда, взаимопроверка выполненной работы в парах. Это дало возможность каждому ученику оценить свои знания, увидеть, что он усвоил, а над чем нужно еще поработать.
В ходе урока все ученики работали активно и с интересом, показали высокий уровень усвоения материала, сформированность умений и навыков, были внимательны, терпимы по отношению друг к другу, излагали изученный материал последовательно, логично.
Считаю, что урок целей достиг. Учащиеся показали хороший уровень знаний об окружности и ее элементах, хорошо усвоили формулы для вычисления длины окружности и научились применять их при решении задач.
Материал, подобранный для урока был доступен для всех учащихся этого класса. Выбранный тип и форма проведения урока себя оправдали

















