Движение плоскости

МОУ гимназия им. А. Л. Кекина

Выполнила:

Иванченко Анна 9 «в»

Учитель:

Иванченко И.А.

• Углубить свои знания по геометрии.
• Узнать виды движения плоскости.
• Применять знания полученные в результате изучения данной темы при решении практических задач.

Введение

• С древних времен с помощью представлений о симметрии человек пытается понять порядок, красоту, совершенство окружающего мира. Изучая математику мы «изучаем саму жизнь».
• В повседневном языке под симметрией понимают чаще всего упорядоченность, гармонию, соразмерность. Кристаллы издавна восхищают нас своим совершенством, строгой симметричностью форм. Симметричные мозаики, фрески, архитектурные ансамбли будят в людях чувство прекрасного, музыкальные и поэтические произведения вызывают восхищение именно своей гармоничностью. В создании общей картины мира с его единством и многообразием свойств неживой и живой природы симметрия оказывает неоценимую услугу.

Историческая справка

• Первым, кто начал доказывать некоторые геометрические предложения, считается древнегреческий математик Фалес Милетский (625-547 г. до н.э.).
• Во времена античной истории идеей движения пользовался и знаменитый Евклид.
• Дальнейшее развитие теории движений связывают с именем французского математика и историка науки Мишеля Шаля (1793-1880).
• В (1849-1925) теорией движения занимался математик Кристиан Феликс Клейн .
• В 1909 г. немецкий математик Фридрих Шур (1856-1932), следуя идеям Фалеса и Клейна, разработал другую систему аксиом геометрии – основанную на рассмотрении движений.

Если каждой точке плоскости ставится в соответствие точка этой же плоскости, то дано отображение плоскости на себя.

С 1

А 1

а

Отображение плоскости на себя, которое сохраняет расстояние между точками называется движением.

А

В 1

В

С

Р

М

N

Теорема: При движении отрезок отображается на отрезок.

N 1

Докажем что MN → М1N1.

1) Р лежит на MN

2) Р переходит в Р1, МР + PN = =MN, М1N1=MN, M1P1=MP и N1P1=NP → M1P1+ N1P1= М1N1

3) P1 лежит на M1N1

Р 1

М 1

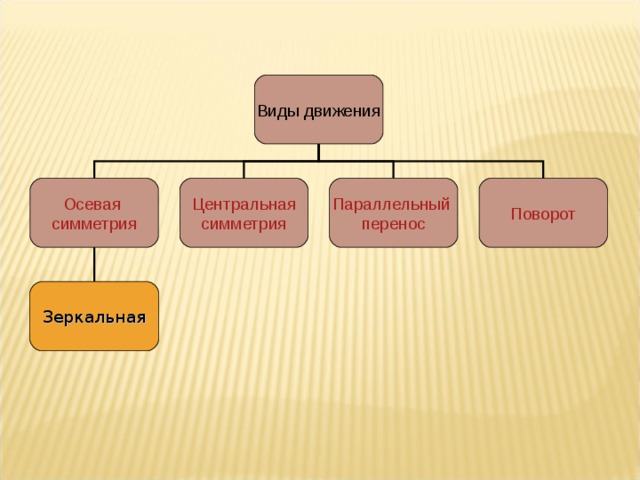
Виды движения

Осевая

симметрия

Центральная

симметрия

Параллельный

перенос

Поворот

Зеркальная

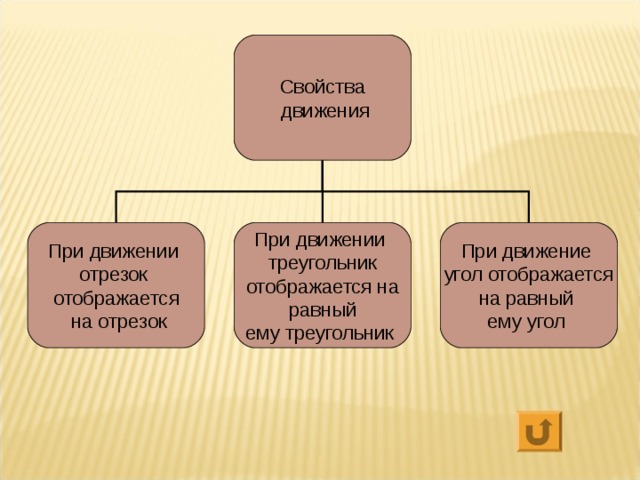
Свойства

движения

При движении

отрезок

отображается

на отрезок

При движении

треугольник

отображается на

равный

ему треугольник

При движение

угол отображается

на равный

ему угол

Осевая симметрия

Осевая симметрия - это такое отображение плоскости на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а

Осевая симметрия:

1. Является движением, т.е сохраняет расстояние между точками.

2. Отрезок переводит в равный ему отрезок.

3. Треугольник переводит в равный ему треугольник.

4. Любое тело переходит в равное ему тело

Для того, чтобы задать осевую симметрию , необходимо задать ось, относительно которой и будет осуществляться эта симметрия

Какие точки называются симметричными относительно данной прямой?

• Две точки А и А 1 называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА 1 и перпендикулярна ему.

Как построить точку симметричную данной относительно прямой L ?

L

А

А 1

L

А

О

А 1

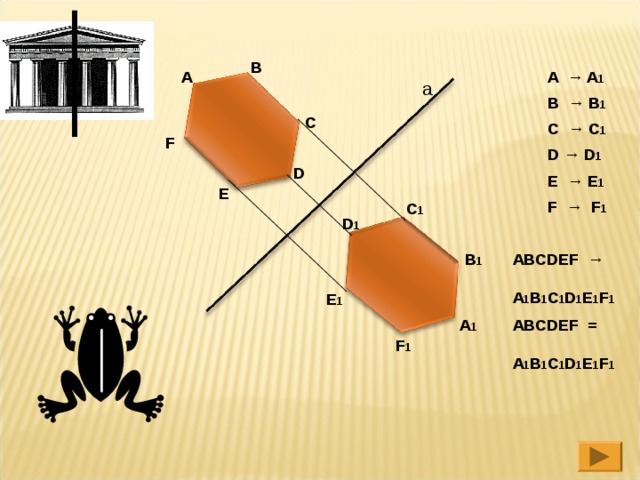
В

A → A 1

B → B 1

C → C 1

D → D 1

E → E 1

F → F 1

А

а

С

F

D

E

С 1

D 1

В 1

ABCDEF → A 1 B 1 C 1 D 1 E 1 F 1

E 1

ABCDEF = A 1 B 1 C 1 D 1 E 1 F 1

А 1

F 1

Докажите, что при осевой симметрии плоскости:

а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси симметрии;

б) прямая, перпендикулярная к оси симметрии, отображается на себя.

Решение :

Обозначим буквой b ось симметрии. Осевая симметрия – движение, поэтому образом прямой a является некоторая прямая a’ .

Пусть а || b . Предположим, что прямые b и а ’ не параллельны. Тогда они имеют общую точку обозначим её М. Так как М принадлежит b , то точка М отображается сама на себя, и, следовательно, М принадлежит а. Отсюда следует, что прямые а и b имеют общую точку М, что противоречит условию а || b . Следовательно, а ' || b .

b

a ’

Решение:

Пусть а перпендикулярна b , М- точка пересечения прямых а и b , а N – точка прямой а, отличная от М. Так как а перпендикулярна b , то N ’ лежит на прямой а. О чевидно, что М ’ , т. е. сама точка М, лежит на прямой а . Таким образом, прямые а и а ` имеют общие точки: M и N' , следовательно они совпадут.

a

N '

М

b

N

Зеркальная симметрия

Зеркальной симметрией называется такое отображение плоскости на себя, при котором любая точка М переходит в симметричную ей относительно прямой а точку М 1.

Симметрия

относительно вертикальной прямой

Симметрия относительно горизонтальной прямой Зеркальная симметрия имеет такие же свойства как и любая симметрия

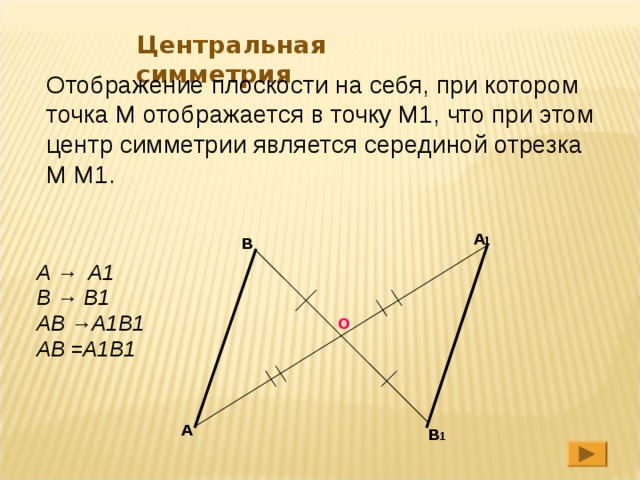
Центральная симметрия

Отображение плоскости на себя, при котором точка М отображается в точку М1, что при этом центр симметрии является серединой отрезка М М1.

А 1

В

A → A1

B → B1

AB →A1B1

AB =A1B1

О

А

В 1

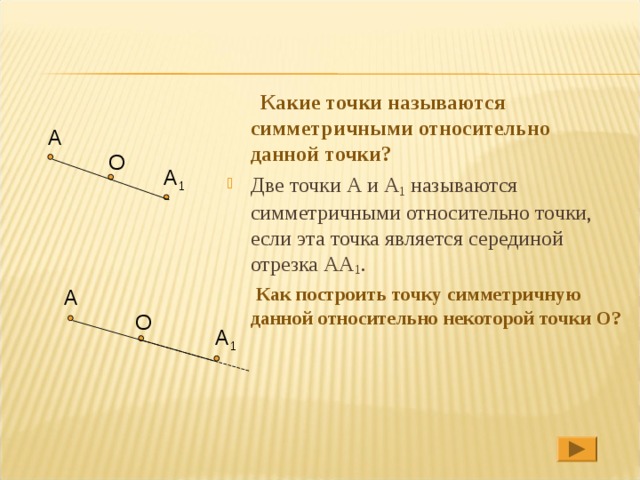
Какие точки называются симметричными относительно данной точки?

• Две точки А и А 1 называются симметричными относительно точки, если эта точка является серединой отрезка АА 1 .

Как построить точку симметричную данной относительно некоторой точки О?

А

О

А 1

А

О

А 1

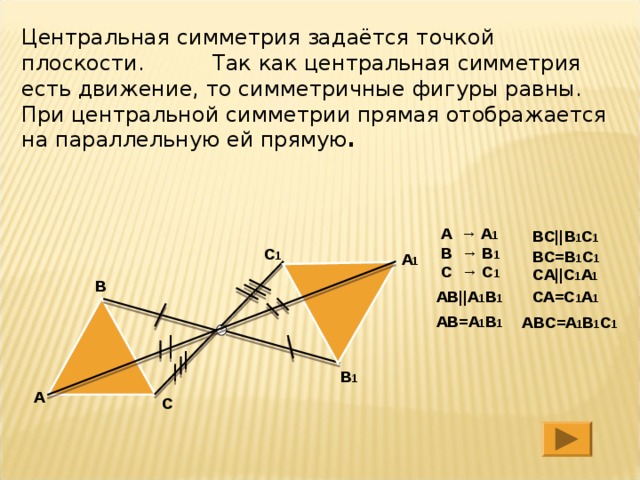
Центральная симметрия задаётся точкой плоскости. Так как центральная симметрия есть движение, то симметричные фигуры равны. При центральной симметрии прямая отображается на параллельную ей прямую .

A → A 1 B → B 1 C → C 1

BC||B 1 C 1

C 1

BC=B 1 C 1

A 1

CA||C 1 A 1

B

CA=C 1 A 1

AB||A 1 B 1

AB=A 1 B 1

ABC=A 1 B 1 C 1

B 1

A

C

Центральная симметрия является частным случаем поворота - это поворот вокруг центра симметрии на угол 180.(рис.1)

Рис. 1

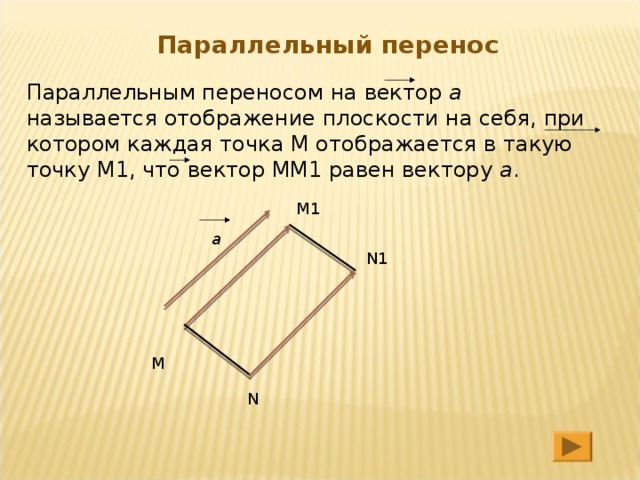
Параллельный перенос

Параллельным переносом на вектор а называется отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что вектор ММ1 равен вектору а .

а

N1

N

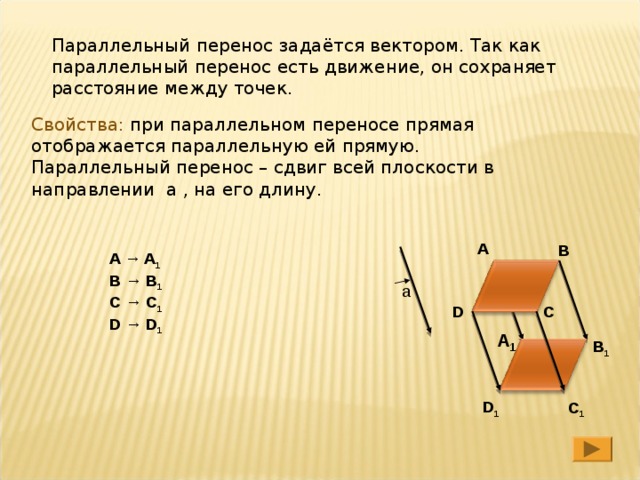
Параллельный перенос задаётся вектором. Так как параллельный перенос есть движение, он сохраняет расстояние между точек.

Свойства: при параллельном переносе прямая отображается параллельную ей прямую.

Параллельный перенос – сдвиг всей плоскости в направлении а , на его длину.

А

В

A → A 1 B → B 1 C → C 1 D → D 1

а

D

С

А 1

В 1

D 1

С 1

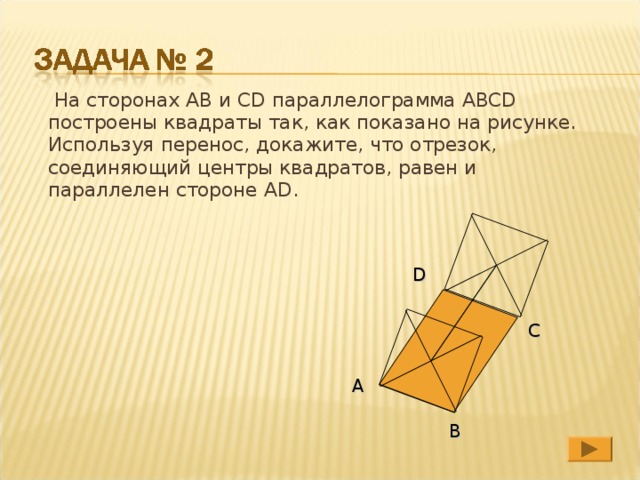
На сторонах АВ и CD параллелограмма ABCD построены квадраты так, как показано на рисунке. Используя перенос, докажите, что отрезок, соединяющий центры квадратов, равен и параллелен стороне AD .

D

C

А

В

Рассмотрим параллельный перенос на вектор AD . Так как ABCD - параллелограмм, то BC=AD , поэтому при этом параллельном переносе точка В отображается в точку С. Отрезки АА1 и DA 2 равны и параллельны, поэтому ADA2A1 - параллелограмм, и, следовательно, А1А2= AD .Таким образом, при рассматриваемом параллельном переносе точка А1 отображается в точку А2, точка В - в точку С, и , значит, отрезок А1В отображается на отрезок А2С. Отсюда следует, что середина О1 отрезка А1В отображается в середину О2 отрезка А2С, т. е. О1О2= AD .

Поэтому О1О2= AD , О1О2 || AD .

A2

O2

D

A1

C

O1

A

B

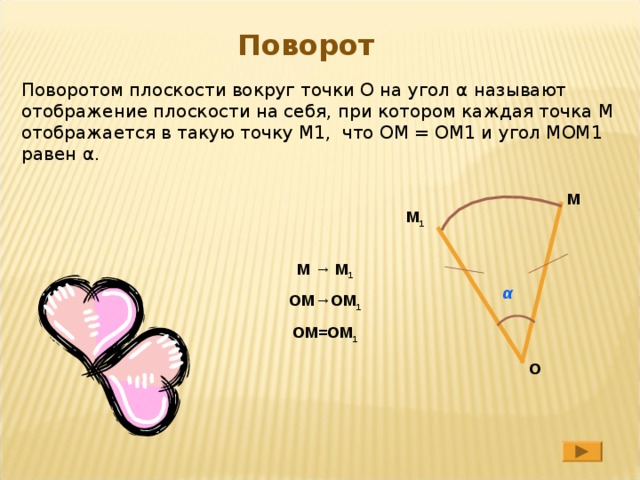
Поворот

Поворотом плоскости вокруг точки О на угол α называют отображение плоскости на себя, при котором каждая точка М отображается в такую точку М1, что ОМ = ОМ1 и угол МОМ1 равен α .

М

М 1

М → М 1

ОМ→ОМ 1

ОМ=ОМ 1

α

О

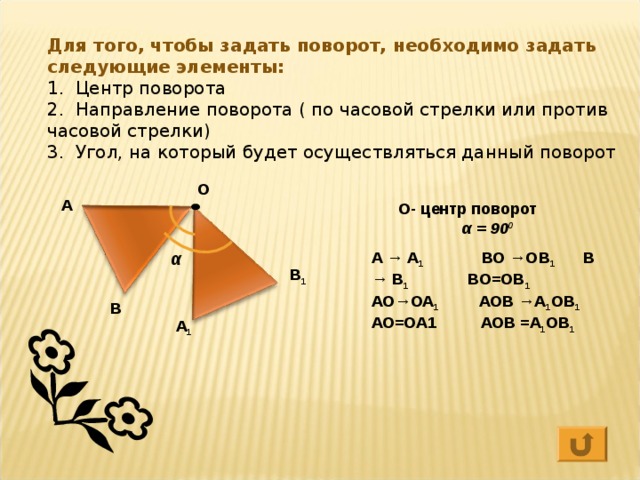
Для того, чтобы задать поворот, необходимо задать следующие элементы:

1. Центр поворота

2. Направление поворота ( по часовой стрелки или против часовой стрелки)

3. Угол, на который будет осуществляться данный поворот

О

А

О- центр поворот α = 90 0

А → А 1 ВО →ОВ 1 В → В 1 ВО=ОВ 1 АО→ОА 1 АОВ →А 1 ОВ 1 АО=ОА1 АОВ =А 1 ОВ 1

α

В 1

В

А 1

Последовательное выполнение двух движений даёт новое движение.

Выясним , какое движение получается в результате последовательного выполнения двух осевых симметрий с различными осями а и в. Возможны два случая:

1. прямые l и m параллельны

2. прямые l и m пересекаются

Обозначим буквой d расстояние между параллельными прямыми l и m и введем систему координат так, чтобы ось Ох совпала с прямой l , а прямая m имела уравнение y = d .

Рассмотрим произвольную точку М с координатами( x ; y ). При симметрии относительно прямой l она перейдёт в точку N с координатами ( x ; - y ). Точка N , в свою очередь , перейдёт в точку М1 , что прямая m окажется серединным перпендикуляром к отрезку NM 1. Следовательно, середина отрезка NM 1 должна иметь координаты ( x ; d ),

а значит, сама точка М1- координаты ( x ; y =2 d ).

Итак, в результате последовательного выполнения двух осевых симметрий произвольная точка М ( x ; y ) перешла в точку М1 ( x ; y +2 d ), т. е. в такую точку М1, что

=

{0; 2 d }.

а

Это означает, что результатом последовательного выполнения

двух осевых симметрий с параллельными осями является параллельный перенос на вектор, перпендикулярный к этим осям, длина которого равна удвоенному расстоянию между осями.

M1(x; y+2d)

У

d

m

M (x ; y)

Х

l

N (x ;-y)

2. Обозначим буквой О точку пересечения прямых l и m и выберем на этих прямых соответственно точки А и В так, чтобы угол АОВ не был тупым.

Возьмём теперь какую – нибудь точку М, отличную от О. Допустим, что она лежит внутри угла АОВ. При симметрии относительно прямой l точка М перейдёт в точку N , что ON = OM и

Поэтому

М1

m

B

M

l

O

A

N

Итак, в результате последовательного выполнения двух симметрий точка О осталось

на месте, а произвольная точка М перешла в точку М1, что

OM1=OM и

Кроме того, направление поворота вокруг точки О от ОМ к ОМ1 такое же, как от ОА к ОВ.

Р езультатом последовательного выполнения двух осевых симметрий с пересекающимися осями является поворот вокруг точки пересечения осей на угол, вдвое больший угла между осями.

В частности, если оси взаимно перпендикулярны, то в результате получится поворот на 180º , т. е. центральная симметрия. Отметим также, что результатом последовательного выполнения двух осевых симметрий с совпадающими осями является, очевидно, тождественное отображение.

Виды движений

Если движение оставляет неподвижными три точки плоскости, не лежащие на одной прямой, это движение- тождественное отображение.

М

А

М1

Если движение оставляет неподвижными две точки плоскости, и не является тождественным отображением, то это движение- осевая симметрия.

М1

В

А

М1

Если движение оставляет неподвижным только одну точку, то это движение- поворот вокруг неподвижной точки.

М

О

М1

Если движение не оставляет ни одной неподвижной точки, то это движение либо последовательное выполнение трех осевых симметрий, оси которых не параллельны друг другу и не пересекаются в одной точке.

А2

А

А1

Вывод

Любое движение представляет собой либо осевую симметрию, либо поворот, либо параллельный перенос, либо последовательное выполнение трех осевых симметрий, оси которых не параллельны друг другу и не проходят через одну точку.

Список литературы

• 1. Л. С. Атанасян. «Дополнительные главы к учебнику геометрии 9 класс» ; Вита пресс, Москва, 2004г
• 2.Л. С. Атанасян. «Геометрия 7-9» Москва «Просвещение» 2003
• 3.В.В. Прасолов « Задачи по планиметрии» Часть 2 Москва наука ,1995
• 4.. А. В. Погорелов «Геометрия 6-10 класс» Москва «Просвещение» 1988г.
• 5. Ресурсы Интернета