РЕШУ ЕГЭ — математика профильная
Вариант № 79337486
1.
i
 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
2.
i
 Найдите квадрат длины вектора
Найдите квадрат длины вектора  +
+ 
3.
i
 Объем куба равен
Объем куба равен  Найдите его диагональ.
Найдите его диагональ.
4.
i
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
5.
i
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
6.
i
Решите уравнение 
7.
i
Найдите значение выражения  при
при 
8.
i
Прямая  является касательной к графику функции
является касательной к графику функции  Найдите b, учитывая, что абсцисса точки касания больше 0.
Найдите b, учитывая, что абсцисса точки касания больше 0.
9.
i
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону  где t − время в секундах, амплитуда
где t − время в секундах, амплитуда  В, частота
В, частота  /с, фаза
/с, фаза  Датчик настроен так, что если напряжение в нeм не ниже чем
Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
10.
i
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
11.
i
 На рисунке изображён график функции
На рисунке изображён график функции  Найдите значение x, при котором
Найдите значение x, при котором 
12.
i
Найдите точку максимума функции  принадлежащую промежутку
принадлежащую промежутку 
13.
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14.
i
В кубе ABCDA1B1C1D1 все ребра равны 6.
а) Докажите, что угол между прямыми AC и BC1 равен 60°.
б) Найдите расстояние между прямыми AC и BC1.
15.
i
Решите неравенство: 
16.
i
Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?
17.
i
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
ЕГЭ 2024 Декабрь Математика Вариант
РЕШУ ЕГЭ — математика профильная
Вариант № 79337486
1.
i
 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
2.
i
 Найдите квадрат длины вектора
Найдите квадрат длины вектора  +
+ 
3.
i
 Объем куба равен
Объем куба равен  Найдите его диагональ.
Найдите его диагональ.
4.
i
Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд начнёт игру с мячом. Команда «Физик» играет три матча с разными командами. Найдите вероятность того, что в этих играх «Физик» выиграет жребий ровно два раза.
5.
i
В Волшебной стране бывает два типа погоды: хорошая и отличная, причём погода, установившись утром, держится неизменной весь день. Известно, что с вероятностью 0,8 погода завтра будет такой же, как и сегодня. Сегодня 3 июля, погода в Волшебной стране хорошая. Найдите вероятность того, что 6 июля в Волшебной стране будет отличная погода.
6.
i
Решите уравнение 
7.
i
Найдите значение выражения  при
при 
8.
i
Прямая  является касательной к графику функции
является касательной к графику функции  Найдите b, учитывая, что абсцисса точки касания больше 0.
Найдите b, учитывая, что абсцисса точки касания больше 0.
9.
i
Датчик сконструирован таким образом, что его антенна ловит радиосигнал, который затем преобразуется в электрический сигнал, изменяющийся со временем по закону  где t − время в секундах, амплитуда
где t − время в секундах, амплитуда  В, частота
В, частота  /с, фаза
/с, фаза  Датчик настроен так, что если напряжение в нeм не ниже чем
Датчик настроен так, что если напряжение в нeм не ниже чем  В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
В, загорается лампочка. Какую часть времени (в процентах) на протяжении первой секунды после начала работы лампочка будет гореть?
10.
i
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
11.
i
 На рисунке изображён график функции
На рисунке изображён график функции  Найдите значение x, при котором
Найдите значение x, при котором 
12.
i
Найдите точку максимума функции  принадлежащую промежутку
принадлежащую промежутку 
13.
i
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14.
i
В кубе ABCDA1B1C1D1 все ребра равны 6.
а) Докажите, что угол между прямыми AC и BC1 равен 60°.
б) Найдите расстояние между прямыми AC и BC1.
15.
i
Решите неравенство: 
16.
i
Жанна взяла в банке в кредит 1,2 млн рублей на срок 24 месяца. По договору Жанна должна вносить в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 2%, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна выплатит банку в течение первого года кредитования?
17.
i
Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.
а) Докажите, что ∠CBE = ∠COE.
б) Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE = 24.
18.
i
Найдите все значения a, при каждом из которых система

имеет ровно два различных решения.
19.
i
На доске написано n чисел ai (i = 1, 2, …, n). Каждое из них не меньше 50 и не больше 150. Каждое из этих чисел уменьшают на ri%. При этом либо ri = 2%, либо число ai уменьшается на 2, то есть становится равным ai − 2. (Какие-то числа уменьшились на число 2, а какие-то — на 2 процента).
а) Может ли среднее арифметическое чисел r1, r2, …, rn быть равным 5?
б) Могло ли так получиться, что среднее арифметическое чисел r1, r2, …, rn больше 2, при этом сумма чисел a1, a2 … an уменьшилась более чем на 2n?
в) Пусть всего чисел 30, а после выполнения описанной операции их сумма уменьшилась на 40. Найдите наибольшее возможное значение среднего арифметического чисел r1, r2, …, rn.
18.
i
Найдите все значения a, при каждом из которых система

имеет ровно два различных решения.
19.
i
На доске написано n чисел ai (i = 1, 2, …, n). Каждое из них не меньше 50 и не больше 150. Каждое из этих чисел уменьшают на ri%. При этом либо ri = 2%, либо число ai уменьшается на 2, то есть становится равным ai − 2. (Какие-то числа уменьшились на число 2, а какие-то — на 2 процента).
а) Может ли среднее арифметическое чисел r1, r2, …, rn быть равным 5?
б) Могло ли так получиться, что среднее арифметическое чисел r1, r2, …, rn больше 2, при этом сумма чисел a1, a2 … an уменьшилась более чем на 2n?
в) Пусть всего чисел 30, а после выполнения описанной операции их сумма уменьшилась на 40. Найдите наибольшее возможное значение среднего арифметического чисел r1, r2, …, rn.







 К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.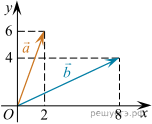 Найдите квадрат длины вектора
Найдите квадрат длины вектора 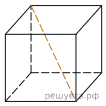 Объем куба равен
Объем куба равен 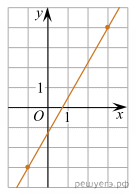 На рисунке изображён график функции
На рисунке изображён график функции