РЕШУ ЕГЭ — математика профильная
Вариант № 79337487
1.
i
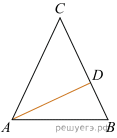
 В треугольнике ABC проведена биссектриса AD и
В треугольнике ABC проведена биссектриса AD и  Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
Найдите меньший угол треугольника ABC. Ответ дайте в градусах.
2.
i
Найдите длину диагонали прямоугольника, вершины которого имеют координаты (2; 1), (2; 4), (6; 1), (6; 4).
3.
i
 Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
4.
i
Фабрика выпускает сумки. В среднем на 190 качественных сумок приходится восемь сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
5.
i
На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.
6.
i
Решите уравнение  В ответе напишите наименьший положительный корень.
В ответе напишите наименьший положительный корень.
7.
i
Найдите  если
если 
8.
i
 Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.
Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).
9.
i
Установка для демонстрации адиабатического сжатия представляет собой сосуд с поршнем, резко сжимающим газ. При этом объeм и давление связаны соотношением  где p (атм.) − давление газа, V − объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
где p (атм.) − давление газа, V − объeм газа в литрах. Изначально объeм газа равен 1,6 л, а его давление равно одной атмосфере. В соответствии с техническими характеристиками поршень насоса выдерживает давление не более 128 атмосфер. Определите, до какого минимального объeма можно сжать газ. Ответ выразите в литрах.
10.
i
Расстояние между городами A и B равно 150 км. Из города A в город B выехал автомобиль, а через 30 минут следом за ним со скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе C и повернул обратно. Когда он вернулся в A, автомобиль прибыл в  Найдите расстояние от A до
Найдите расстояние от A до  Ответ дайте в километрах.
Ответ дайте в километрах.
11.
i
 На рисунке изображён график функции
На рисунке изображён график функции  Найдите значение x, при котором
Найдите значение x, при котором 
12.
i
Найдите точку максимума функции 
13.
i
а) Решите уравнение: 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
14.
i
В правильной треугольной призме ABCA1B1C1 все рёбра равны 2. Точка M — середина ребра AA1.
а) Докажите, что прямые MB и B1C перпендикулярны.
б) Найдите расстояние между прямыми MB и B1C.
15.
i
Решите неравенство: 
16.
i
В 1-е классы поступает 45 человек: 20 мальчиков и 25 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом ― 23. После распределения посчитали процент девочек в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
17.
i
На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.
а) Докажите, что точки A, B, K и E лежат на одной окружности.
б) Найдите радиус этой окружности, если AB = 12, CH = 5.
18.
i
Найдите все значения a, при каждом из которых уравнение

имеет хотя бы одно решение, меньшее 2.
19.
i
Пусть q — наименьшее общее кратное, а d — наибольший общий делитель натуральных чисел x и y, удовлетворяющих равенству 3x = 8y − 29.
а) Может ли  быть равным 170?
быть равным 170?
б) Может ли  быть равным 2?
быть равным 2?
в) Найдите наименьшее значение 







 В треугольнике ABC проведена биссектриса AD и
В треугольнике ABC проведена биссектриса AD и  Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.
Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.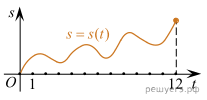 Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.
Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.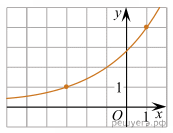 На рисунке изображён график функции
На рисунке изображён график функции 


















