ЕГЭ. Информатика. Задание 27.

Подготовка к ЕГЭ Задание 27

Составитель: учитель информатики

высшей квалификационной категории

МАОУ «СОШ № 10» г. Миасса

Абрамова И.Б.

Кодификатор элементов содержания и требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по информатике и ИКТ

Возможные алгоритмические задачи для подраздела 1.1 перечня требований к уровню подготовки выпускников, достижение которых проверяется на едином государственном экзамене по информатике и ИКТ.

• Нахождение минимума и максимума двух, трех, четырех данных чисел без использования массивов и циклов.
• Нахождение всех корней заданного квадратного уравнения.
• Запись натурального числа в позиционной системе с основанием, меньшим или равным 10. Обработка и преобразование такой записи числа.
• Нахождение сумм, произведений элементов данной конечной числовой последовательности (или массива).
• Использование цикла для решения простых переборных задач (поиск наименьшего простого делителя данного натурального числа, проверка числа на простоту и т.д.).
• Заполнение элементов одномерного и двумерного массивов по заданным правилам.
• Операции с элементами массива. Линейный поиск элемента. Вставка и удаление элементов в массиве. Перестановка элементов данного массива в обратном порядке. Суммирование элементов массива. Проверка соответствия элементов массива некоторому условию.
• Нахождение второго по величине (второго максимального или второго минимального) значения в данном массиве за однократный просмотр массива.
• Нахождение минимального (максимального) значения в данном массиве и количества элементов, равных ему, за однократный просмотр массива.
• Операции с элементами массива, отобранных по некоторому условию (например, нахождение минимального четного элемента в массиве, нахождение количества и суммы всех четных элементов в массиве).
• Сортировка массива.
• Слияние двух упорядоченных массивов в один без использования сортировки.
• Обработка отдельных символов данной строки. Подсчет частоты появления символа в строке.
• Работа с подстроками данной строки с разбиением на слова по пробельным символам. Поиск подстроки внутри данной строки, замена найденной подстроки на другую строку.

Задача 1 (ИНФ_ДЕМО 2017)

Вам предлагается два задания с похожими условиями:

• задание А ( 2 балла) и
• задание Б ( 4 балла).

Вы можете решать оба задания или одно из них по своему выбору.

Итоговая оценка выставляется как максимальная из оценок за задания А и Б.

ИНФ-ДЕМО-2017

Задание А

Задание Б

Имеется набор данных, состоящий из 6 пар положительных целых чисел.

Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.

Имеется набор данных, состоящий из пар положительных целых чисел.

Входные данные

Необходимо выбрать из каждой пары ровно одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.

На вход программе подаётся шесть строк, каждая из которых содержит два натуральных числа, не превышающих 10 000.

Входные данные

Напишите программу для решения этой задачи. В этом варианте задания оценивается только правильность программы, время работы и размер использованной памяти не имеют значения.

На вход программе в первой строке подаётся количество пар N (1 ≤ N ≤ 100 000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.

Напишите программу для решения этой задачи. Постарайтесь сделать программу эффективной по времени и используемой памяти (или хотя бы по одной из этих характеристик).

ИНФ-ДЕМО-2017

• Программа считается эффективной по времени , если время работы программы пропорционально количеству пар чисел N, т.е. при увеличении N в k раз время работы программы должно увеличиваться не более чем в k раз.
• Программа считается эффективной по памяти , если размер памяти, использованной в программе для хранения данных, не зависит от числа N и не превышает 1 килобайта .

Задание Б

• Максимальная оценка за правильную программу, эффективную по времени и памяти – 4 балла.
• Максимальная оценка за правильную программу, эффективную по времени, но неэффективную по памяти – 3 балла .

Задание А и Б

• Как в варианте А, так и в варианте Б программа должна напечатать одно число – максимально возможную сумму, соответствующую условиям задачи или 0, если такую сумму получить нельзя.
• НАПОМИНАЕМ! Не забудьте указать, к какому заданию относится каждая из представленных Вами программ.

Задание А и Б

• Перед текстом программы кратко опишите Ваш алгоритм решения
• Укажите использованный язык программирования и его версию (например, Free Pascal 2.6.4).

Критерии оценивания задания А

При решении задачи A программа верно находит требуемую сумму для любых 6 пар исходных данных.

2

Не выполнены условия, позволяющие поставить 2 балла . Из описания алгоритма и общей структуры программы видно, что экзаменуемый в целом правильно представляет путь решения задачи.

1

Критерии оценивания задания Б

Программа правильно работает для любых соответствующих условию входных данных и при этом эффективна как по времени, так и по памяти, т.е. не используются массивы и другие структуры данных (в том числе стек рекурсивных вызовов), размер которых зависит от количества входных элементов, а время работы пропорционально этому количеству. Возможно использование массивов при условии, что в них в каждый момент времени хранится фиксированное количество элементов, требующих для хранения меньше 1Кб.

4

Критерии оценивания задания Б

Программа в целом работает правильно для любых входных данных произвольного размера.

Время работы пропорционально количеству введённых чисел.

3

Правильно указано, какие величины должны вычисляться по ходу чтения элементов последовательности чисел.

Используемая память, возможно, зависит от количества прочитанных чисел

(например, входные данные запоминаются в массиве или другой структуре данных).

Критерии оценивания задания Б

Программа работает в целом верно,

эффективно или нет.

2

Из описания алгоритма и общей структуры программы видно, что экзаменуемый в целом правильно представляет путь решения задачи.

Программа может быть неэффективна по времени и по памяти, например, все числа запоминаются в массиве и перебираются все возможные суммы, то есть по сути реализовано решение задачи А без ограничений на количество ввёденных пар.

1 балл ставится также за решения, верные лишь в частных случаях.

1

Решаем задачу как получится.

Вариант Б. Идея решения.

Чтобы получить максимально возможную сумму, будем брать из каждой пары самое большое число. Если полученная при этом сумма будет делиться на 3, её необходимо уменьшить. Для этого достаточно в одной из пар, где числа имеют разные остатки при делении на 3, заменить ранее выбранное число на другое число из той же пары. При этом разница между числами в паре должна быть минимально возможной. Если во всех парах оба числа имеют одинаковый остаток при делении на 3, получить нужную сумму невозможно.

Задание Б. Алгоритм решения.

Программа читает все данные один раз.

В каждой паре определяется большее число Max и разность между бόльшим и меньшим числами пары d.

После обработки очередной пары программа хранит два числа:

• s – сумму всех максимальных элементов прочитанных пар и
• D_min – наименьшую возможную разность , не кратную 3.

Окончательным ответом будет значение s, если оно не делится на 3, и s – D_min в противном случае.

Если s делится на 3, а D _min не определено (разность между числами во всех парах кратна 3), ответ в соответствии с условиями задачи считается равным 0.

Задание Б. Язык программирования PascalABC.

сonst aMax = 10000 ; {наибольшее возможное число в исх. данных}

Var i, N : longint; {количество пар}

a, b : longint; {пара чисел}

s : longint; {сумма выбранных чисел}

Max : longint; {большее значение в паре}

Min : longint; {меньшее значение в паре}

d : longint; {Max – Min в паре}

D_min : longint; {минимальная разница Max – Min, не кратная 3}

{ для всех прочитанных пар }

Begin

s := 0;

D_min := aMax + 1;

readln(N);

b then begin Max := a; Min := b end else begin Max := b; Min := a end; s := s + Max; if ((Max - Min) mod 3 0) and (Max - Min end; If (s mod 3 = 0) then If (D_min aMax) then s := 0 else s := s – D_min; writeln(s); end. " width="640"

Задание Б. Язык программирования PascalABC.

for i := 1 to N do begin

readln(a, b);

if a b then begin Max := a; Min := b end

else begin Max := b; Min := a end;

s := s + Max;

if ((Max - Min) mod 3 0) and (Max - Min

end;

If (s mod 3 = 0) then

If (D_min aMax) then s := 0

else s := s – D_min;

writeln(s);

end.

sMax) then sMax := s ; end; writeln(sMax); end. " width="640"

Задание А. Полный перебор.

var a: array[1..6, 1..2] of longint; s, sMax, i1, i2, i3, i4, i5, i6: longint;

Begin

for i1 := 1 to 6 do readln(a[i1,1], a[i1,2]);

sMax := 0;

for i1:=1 to 2 do

for i2:=1 to 2 do

for i3:=1 to 2 do

for i4:=1 to 2 do

for i5:=1 to 2 do

for i6:=1 to 2 do begin

s:=a[1,i1]+a[2,i2]+a[3,i3]+a[4,i4]+a[5,i5]+a[6,i6];

if (s mod 3 0) and (s sMax) then sMax := s ;

end;

writeln(sMax);

end.

Вариации на тему Задачи 1

Задача 2. (Т.Ф. Хирьянов)

По каналу связи передаются положительные целые числа (0 – признак конца ввода, чисел не менее двух и не более 10000).

Затем контрольное значение равное максимальному произведению двух чисел, которое кратно 7, но не кратно 49. Если такое произведение получить нельзя, то контрольное значение равно 1.

Посчитайте количество переданных чисел, контрольное значение для полученных чисел и выведите отчёт:

• количество чисел, полученное контрольное значение, посчитанное контрольное значение, вывод: совпали или не совпали контрольные значения.
• количество чисел,
• полученное контрольное значение,
• посчитанное контрольное значение,
• вывод: совпали или не совпали контрольные значения.

https://www.youtube.com/watch?v=mweuFxP4o-k&list=PL66kIi3dt8A5slbxnwIjiYHloR1VGE-UJ&index=43

Источник https://www.youtube.com/watch?v=mweuFxP4o-k&list=PL66kIi3dt8A5slbxnwIjiYHloR1VGE-UJ&index=43

Примеры:

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А, а переданное значение контрольной суммы в переменную Checksum .
• Для подсчёта количества чисел в потоке ввода заводим переменную N и присваиваем ей начальное значение 0.
• Максимальное произведение кратное 7, но не кратное 49 будем записывать в переменную R и присвоим ей начальное значение 1.
• В цикле перебираем все возможные пары чисел и, если их произведение кратно 7 и не кратно 49 и при этом больше чем записано в R, записываем в R новый максимум, равный произведению данных чисел.
• Выводим ответ, согласно условию задачи.

Задание А. Язык программирования PascalABC .

Var A : array[1..10000] of longint;

N, x, R, Checksum, i, j, P : longint;

Begin

// ввод данных

N :=0;

readln(х);

while x 0 do begin

N := N + 1;

a[N] := x;

readln(х);

end;

readln(Checksum);

R) then R:= P; end; Writeln(‘Введено чисел ’, N); // вывод Writeln(‘Переданное контрольное значение ’, Checksum ); Writeln(‘Вычисленное контрольное значение ’, R); If R = Checksum then w riteln(‘Значения совпали’) else w riteln(‘Значения не совпали’); end. " width="640"

Задание А. Продолжение программы.

R := 1; // вычисление контрольного значения

for i := 1 to N - 1 do

for j := i + 1 to N do begin

P := A[i] * A[j];

if (P mod 7 = 0) and (P mod 49 0) and (P R) then R:= P;

end;

Writeln(‘Введено чисел ’, N); // вывод

Writeln(‘Переданное контрольное значение ’, Checksum );

Writeln(‘Вычисленное контрольное значение ’, R);

If R = Checksum then w riteln(‘Значения совпали’)

else w riteln(‘Значения не совпали’);

end.

Задание Б. Алгоритм решения.

Произведение двух чисел кратно 7 и не кратно 49, если:

• один из сомножителей кратен 7, но не кратен 49;
• второй сомножитель не кратен 7.

Произведение будет максимальным если перемножить самое большое число не кратное 7 и самое большое число кратное 7, но не кратное 49 из потока ввода. По мере поступления чисел будем их считать (переменная N , начальное значение 0) и искать максимальные значения среди чисел

• не кратных 7 (переменная max , нач. значение 0)
• кратных 7, но не кратных 49 (переменная max7 , нач. значение 0)

Вычисленная контрольная сумма R = max * max7, будет равна 0 если не было чисел не кратных 7 или кратных 7, но не кратных 49 и тогда контрольная сумма R должна быть равна 1 по условию задачи.

Выводим ответы согласно условию задачи.

Задание Б. Язык программирования PascalABC.

Var

x, N, max, max7, R, Checksum : longint;

Begin

N:=0; // количество переданных чисел

max:=0; // максимальное число не кратное 7

max7:=0; // максимальное число кратное 7, но

// не кратное 49

readln(х); // x − текущее число из потока // ввода

max7) then max7 := x; if (x mod 7 0) and (x max) then max := x; readln(х); end; R := max * max7; If R = 0 then R := 1; readln(Checksum); Writeln(‘Введено чисел ’, N); Writeln(‘Переданное контрольное значение ’, Checksum ); Writeln(‘Вычисленное контрольное значение ’, R); If R = Checksum then w riteln(‘Значения совпали’) else w riteln(‘Значения не совпали’); end. " width="640"

Задание Б. Продолжение программы.

while x 0 do begin

N := N + 1;

if (x mod 7 = 0) and (x mod 49 0) and (x max7) then max7 := x;

if (x mod 7 0) and (x max) then max := x;

readln(х);

end;

R := max * max7; If R = 0 then R := 1;

readln(Checksum);

Writeln(‘Введено чисел ’, N);

Writeln(‘Переданное контрольное значение ’, Checksum );

Writeln(‘Вычисленное контрольное значение ’, R);

If R = Checksum then w riteln(‘Значения совпали’)

else w riteln(‘Значения не совпали’);

end.

Задача 3. (ИНФ_ДЕМО 2014)

По каналу связи передаётся последовательность положительных целых чисел, все числа не превышают 1000. Количество чисел известно и не превышает 100000. Затем передаётся контрольное значение последовательности – наибольшее число R, удовлетворяющее следующим условиям:

1) R – произведение двух различных переданных элементов последовательности («различные» означает, что не рассматриваются квадраты переданных чисел; допускаются произведения различных элементов последовательности, равных по величине);

2) R делится на 21.

Если такого числа R нет, то контрольное значение полагается равным 0.

Программа должна напечатать отчёт по следующей форме:

Вычисленное контрольное значение: …

Контроль пройден (или – Контроль не пройден)

Задача 3. Продолжение .

На вход программе в первой строке подаётся количество чисел N. В каждой из последующих N строк записано одно натуральное число, не   превышающее 1000. В последней строке записано контрольное значение.

Пример входных данных :

6

70

21

997

7

9

300

21000

Пример выходных данных для приведённого выше примера входных данных:

Вычисленное контрольное значение: 21000

Контроль пройден

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А, а переданное значение контрольной суммы в переменную Checksum .
• Максимальное произведение кратное 21 будем записывать в переменную R и присвоим ей начальное значение 0.
• В цикле перебираем все возможные пары чисел и, если их произведение кратно 21 и при этом больше чем записано в R, записываем в R новый максимум, равный произведению данных чисел.
• Выводим ответ, согласно условию задачи.

R) then R := a[i]*a[j]; writeln(‘Вычисленное контр.значение ’,R); if R = Checksum then writeln(‘Контроль пройден’) else writeln(‘Контроль не пройден’); end. " width="640"

Задание А. Язык программирования PascalABC .

var N, i, j, R, Checksum : integer;

a: array[1..100000] of integer;

begin

readln(N);

for i:=1 to N do readln(a[i]);

readln(Checksum); R := 0;

for i:=1 to N-1 do

for j:=i+1 to N do

if (a[i]*a[j] mod 21 = 0) and (a[i]*a[j] R)

then R := a[i]*a[j];

writeln(‘Вычисленное контр.значение ’,R);

if R = Checksum then

writeln(‘Контроль пройден’)

else writeln(‘Контроль не пройден’);

end.

Задание Б. Алгоритм решения.

Программа читает все входные данные один раз, не запоминая все данные в массиве. Программа для прочитанного фрагмента входной последовательности хранит значения четырёх величин:

• М7 – самое большое число, кратное 7, но не кратное 3;
• M3 – самое большое число, кратное 3, но не кратное 7;
• M21 – самое большое число, кратное 21;
• МAX – самое большое число среди всех элементов последовательности, отличное от М21 (если число М21 встретилось более одного раза и оно же является максимальным, то MAX = M21).

После того как все данные прочитаны, искомое контрольное значение вычисляется как максимум из произведений

(М21 * MAX) и (М7 * М3).

M7) then M7 := a; if (a mod 3 = 0) and (a mod 7 0) and (a M3) then M3 := a; if (a mod 21 = 0) and (a M21) then begin if M21 MAX then MAX := M21; M21 := a; end else if a MAX then MAX := a; end; " width="640"

Задание Б. Язык программирования PascalABC .

var M7, M3, M21, R, MAX, a, res, i, N: longint;

begin

M7 := 0; M3 := 0; M21 := 0; MAX := 0;

readln(N);

for i := 1 to N do begin

readln(a);

if (a mod 7 = 0) and (a mod 3 0) and (a M7)

then M7 := a;

if (a mod 3 = 0) and (a mod 7 0) and (a M3)

then M3 := a;

if (a mod 21 = 0) and (a M21) then begin

if M21 MAX then MAX := M21;

M21 := a;

end

else

if a MAX then MAX := a;

end;

Задание Б. Продолжение программы.

readln(R);

if (M7*M3

res := M21*MAX

else res := M7*M3;

writeln('Вычисленное контр. значение: ',res);

if R = res then writeln('Контроль пройден')

else writeln('Контроль не пройден');

end.

Задача ИНФ_ДЕМО 2018

На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности (элементы пары не обязаны стоять в последовательности рядом, порядок элементов в паре не важен). Необходимо определить количество пар, для которых произведение элементов делится на 26.

В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 1000). В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна напечатать одно число: количество пар, в которых произведение элементов кратно 26.

Пример входных данных:

4

2

6

13

39

Пример выходных данных для приведённого выше примера входных данных: 4

Пояснение. Из четырёх заданных чисел можно составить 6 попарных произведений: 2·6, 2·13, 2·39, 6·13, 6·39, 13·39 (результаты: 12, 26, 78, 78, 234, 507). Из них на 26 делятся 4 произведения (2·13=26; 2·39=78; 6·13=78; 6·39=234).

Задача 4 . (аналог ИНФ_ДЕМО 2018, Д.В. Богданов)

Дан набор из N натуральных чисел. Необходимо определить количество пар элементов (a i , a j ) этого набора, в которых 1  i

В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 10000). В каждой из последующих N строк записано одно натуральное число, не превышающее 1000.

Пример входных данных:

4

7

5

6

12

Пример выходных данных для приведённого выше примера входных данных:

5

В приведённом наборе из 4 чисел имеются пять пар (7, 6), (5, 6), (7, 12), (5, 12), (6, 12), произведение элементов которых кратно 6.

Источник http://kpolyakov.spb.ru/school/ege.htm сайт К.Ю. Полякова , автор Д.В. Богданов, задача № 75, аналогичная задача в ДЕМО 2018

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А.
• Для подсчёта количества пар в которых произведение кратно 6 заводим переменную count и присваиваем ей начальное значение 0.
• В цикле перебираем все возможные пары и, если их произведение кратно 6, увеличиваем count на 1.
• После цикла, в count будет подсчитано количество пар элементов, произведение которых кратно 6. Его и выводим.

Задание А. Язык программирования PascalABC.

var N, i, j, count : integer;

a: array[1..10000] of integer;

begin

readln(N);

for i:=1 to N do

readln(a[i]);

count := 0;

for i:=1 to N-1 do

for j:=i+1 to N do

if a[i]*a[j] mod 6 = 0 then

count := count + 1;

writeln(count);

end.

Задание Б. Способ 1. Алгоритм решения.

Произведение двух чисел кратно 6, если:

• один из сомножителей кратен 6 (второй может быть любым);
• ни один из сомножителей не кратен 6, но один из сомножителей кратен 2, а другой кратен 3.

По мере поступления чисел будем накапливать количество таких, которые кратны 2, кратны 3 и кратны 6.

Очередное число образует пары с предшествующими числами, при этом возможны следующие случаи:

• число кратно 6, образует пары со всеми числами;
• кратно 2, но не 3, образует пары с числами, кратными 3;
• кратно 3, но не 2, образует пары с числами, кратными 2;
• не кратно 2 и не кратно 3, образует пары с числами, кратными 6.

Определение, к какому случаю относится число, и подсчёт количества пар будем производить в цикле.

Задание Б. Язык программирования PascalABC.

var i, a, ans, k, k2, k3, k6 : longint;

begin

readln(k);

ans:=0; {ответ}

k2:=0; {количество чисел кратных 2, но не кратных 6}

k3:=0; {количество чисел кратных 3, но не кратных 6}

k6:=0; {количество чисел кратных 6}

Задание Б. Продолжение программы.

for i := 1 to k do begin

readln(a); { очередное число}

if a mod 6 = 0 then begin

{если число кратно 6, то оно составляет пару

со всеми введенными ранее числами}

ans := ans + i - 1;

k6 := k6 + 1;

end

else if a mod 3 = 0 then begin

{иначе, если число кратно 3, то оно составляет пару со всеми ранее введенными числами кратными 2}

a ns := ans + k2 + k6 ;

k3 := k3 + 1;

end

Задание Б. Окончание программы.

else if a mod 2 = 0 then begin

{иначе, если число кратно 2, то оно составляет пару со всеми ранее введенными числами кратными 3}

a ns := ans + k3 + k6 ;

k2:=k2+1;

end

else

{иначе (если не кратны 2, 3, 6), то оно составляет пару с числами кратными 6}

a ns := ans + k6 ;

end;

writeln(ans);

end.

Задание Б. Способ 2. Алгоритм решения.

По мере поступления чисел будем накапливать количество таких, которые

• кратны 6 (k6),
• кратны 3, но не кратны 6 (k3) и
• кратны 2, но не кратны 6 (k2).

Каждое число учитывается только в одном из счётчиков.

Произведение двух чисел кратно 6, если:

• оба сомножителя кратны 6, таких пар k6 * (k6 - 1) div 2
• один из сомножителей кратен 6, а другой нет, таких пар k6 * (k - k6)
• ни один из сомножителей не кратен 6, но один из сомножителей кратен 2, а другой кратен 3 , таких пар k2 * k3 .

Искомое количество пар вычисляется по формуле

k6 * (k6 - 1) div 2 + k6 * (k - k6) + k2 * k3.

Можно считать и другими способами.

Задание Б. Язык программирования PascalABC.

var i, a, k, k2, k3, k6 : longint;

begin

k2:=0; k3:=0; k6:=0;

readln(k);

for i := 1 to k do begin

readln(a);

if a mod 6 = 0 then inc(k6)

else if a mod 3 = 0 then inc(k3)

else if a mod 2 = 0 then inc(k2) ;

end;

writeln(k6*(k6-1) div 2 + k6*(k-k6) + k2*k3);

end.

Задача 5. (автор Д.В. Богданов)

Дан набор из N натуральных чисел. Необходимо определить количество пар элементов ( a i , a j ) этого набора, в которых 1  i j  N и сумма элементов кратна 12.

В первой строке входных данных задаётся количество чисел N (1 ≤ N ≤ 10000). В каждой из последующих N строк записано одно натуральное число, не превышающее 1000.

Пример входных данных:

5

7

5

6

12

24

Пример выходных данных для приведённого выше примера: 2

В приведённом наборе из 5 чисел имеются две пары (7, 5) и (12, 24), сумма элементов которых кратна 12.

Источник http://kpolyakov.spb.ru/school/ege.htm сайт К.Ю. Полякова , автор Д.В. Богданов, задача № 77

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А.
• Для подсчёта количества пар в которых сумма кратна 12 заводим переменную count и присваиваем ей начальное значение 0.
• В цикле перебираем все возможные пары и, если их сумма кратна 12, добавляем 1 в count.
• После цикла, в count будет подсчитано количество пар элементов, сумма которых кратна 12.
• Выводим ответ, который записан в count.

Задание А. Язык программирования PascalABC.

var N, i, j: integer;

count: longint;

a: array[1..10000] of integer;

begin

readln(N);

for i:=1 to N do

readln(a[i]);

count := 0; // инициализация

for i:=1 to N-1 do

for j:=i+1 to N do

if (a[i] + a[j]) mod 12 = 0 then

count := count + 1;

writeln(count);

end.

Задание Б. Алгоритм решения.

• Если сумма двух чисел делится на 12, то сумма остатков от деления этих чисел на 12 также делится на 12, то есть равна 0 либо 12. Поэтому заводим массив счётчиков чисел с одинаковыми остатками от деления на 12 ( rem[0..11] ) и при вводе очередного числа увеличиваем счётчик, соответствующий полученному остатку от деления на 12.
• Если число делится на 12 (остаток 0), то оно образует пару со всеми числами, которые делятся на 12, кроме самого себя, таких сочетаний rem[0]*(rem[0]-1) , но при этом каждая пара подсчитана дважды, то есть это произведение нужно разделить на 2. Аналогичная ситуация с теми числами, которые делятся на 6, количество соответствующих пар находим как rem[6]*(rem[6]-1) div 2 .
• Количество остальных подходящих пар считаются по формуле rem[i]*rem[12-i]. Чтобы не получить дублирование пар, будем в цикле перебирать только остатки, меньшие 6.

Задание Б. Язык программирования PascalABC .

var rem: array[0..11] of integer;

N, i, x, count: longint;

begin

for i:=0 to 11 do rem[i]:= 0;

readln(N);

for i := 1 to N do begin

readln(x);

inc(rem[x mod 12])

end;

count := (rem[0]*(rem[0]-1)+rem[6]*(rem[6]-1))div 2;

for i:=1 to 5 do

count := count + rem[i]*rem[12-i];

writeln(count)

end.

Задача 6. (ИНФ_ДЕМО 2015)

На спутнике «Фотон» установлен прибор, предназначенный для измерения энергии космических лучей. Каждую минуту прибор передаёт по каналу связи неотрицательное вещественное число – количество энергии, полученной за последнюю минуту, измеренное в условных единицах. Временем, в течение которого происходит передача, можно пренебречь. Необходимо найти в заданной серии показаний прибора минимальное произведение двух показаний, между моментами передачи которых прошло не менее 6 минут . Количество энергии, получаемое прибором за минуту, не превышает 1000 условных единиц. Общее количество показаний прибора в серии не превышает 10 000.

Демо 2016

6. В каждой из следующих N строк задаётся одно неотрицательное вещественное число – очередное показание прибора. Пример входных данных: Программа должна вывести одно число – описанное в условии произведение. 11 Пример выходных данных для приведённого примера входных данных: 12 45.3 48 5.5 4 25 23 21 20 10 12 26 Демо 2016 " width="640"

Задача 6. Продолжение.

Входные данные представлены следующим образом. В первой строке задаётся число N – общее количество показаний прибора. Гарантируется, что N 6. В каждой из следующих N строк задаётся одно неотрицательное вещественное число – очередное показание прибора.

Пример входных данных:

Программа должна вывести одно число – описанное в условии произведение.

11

Пример выходных данных для приведённого примера входных данных:

12

45.3

48

5.5

4

25

23

21

20

10

12

26

Демо 2016

Задание A. Алгоритм решения .

• Сохраняем все исходные данные в массив А.
• Заведём переменную m для поиска минимального значения произведения и присвоим ей начальное значение 1000*1000+1.
• В цикле перебираем все возможные пары значений и, если между моментами передачи показаний прошло не менее 6 минут и их произведение меньше чем m, записываем это произведение в m.
• Выводим ответ, который записан в m.

=6) and (a[i]*a[j] then m := a[i]*a[j]; writeln(m); end. " width="640"

Задание А. Язык программирования PascalABC.

var N, i, j: integer;

m: real;

a: array[1..10000] of real;

Begin

// ввод данных

readln(N);

for i:=1 to N do readln(a[i]);

// поиск минимального произведения двух показаний, между моментами передачи которых прошло не менее 6 минут

m:= 1000*1000+1;

for i:=1 to N-1 do

for j:=i+1 to N do

if (j-i=6) and (a[i]*a[j] then

m := a[i]*a[j];

writeln(m);

end.

Задание А. Способ 2.

Const s = 6 ;

var N, i, j: integer;

m: real;

a: array[1..10000] of real;

Begin

// ввод данных

readln(N);

for i:=1 to N do readln(a[i]);

// поиск минимального произведения двух показаний, между моментами передачи которых прошло не менее 6 минут

m:= 1000*1000+1;

for i:=1 to N-s do

for j:= i+s to N do

if (a[i]*a[j]

m := a[i]*a[j];

writeln(m);

end.

6), минимальное значение от начала данных до элемента (i-6) включительно (переменная mn). Затем нужно умножать каждый элемент, начиная с седьмого, на значение этого минимума и выбрать наименьшее из этих произведений (переменная m). " width="640"

Задание Б. Способ 1 на 3 балла. Алгоритм решения .

• Чтобы произведение было минимальным надо текущее значение умножать на минимальное из всех предшествующих, отстоящих от текущего на 6 и более показаний и выбирать из этих произведений минимальное.
• Сохраняем все исходные данные в массив А.
• Для построения программы, эффективной по времени , нужно определить для каждого элемента входных данных, начиная с седьмого (i, i 6), минимальное значение от начала данных до элемента (i-6) включительно (переменная mn). Затем нужно умножать каждый элемент, начиная с седьмого, на значение этого минимума и выбрать наименьшее из этих произведений (переменная m).

Задание Б. Язык программирования PascalABC .

const s = 6; {требуемое расстояние между показаниями}

var

N, i : integer;

a: array[1..10000] of real;

mn: real ; {минимальное введенное число без s последних}

m: real; {минимальное значение произведения}

begin

readln(N);

for i:=1 to N do readln(a[i]);

mn := 1000 + 1;

m := 1000 * 1000 + 1;

for i := s + 1 to N do begin

if a[i-s]

if a[i] * mn

end;

writeln(m); end.

Задание Б. Способ 2 на 4 балла. Алгоритм решения.

• Чтобы произведение было минимальным надо текущее значение умножать на минимальное из всех предшествующих, отстоящих от текущего на 6 и более показаний и выбирать из этих произведений минимальное. Каждое текущее показание используется после ввода ещё 6 элементов и после этого становится ненужным, поэтому достаточно хранить 6 последних показаний в массиве A.
• В цикле считываем показания прибора, сохраняя 6 последних в массиве А.
• Перед поступлением очередного показания (х) готовим для него минимум, т.е. проверяем, не будет ли А[1] меньше записанного минимума (mn) и если это так, то обновляем mn.
• Читаем очередное показание и проверяем произведение x*mn. Если оно меньше минимального сохранённого в m, то обновляем m.
• Сдвигаем элементы вспомогательного массива влево и последним записываем текущее показание.
• После цикла минимальное произведение будет записано в переменной m, её и печатаем.

Задание Б. Язык программирования PascalABC .

const s = 6; //требуемое расстояние между показаниями

var

N, i, j : integer;

a: array[1..s] of real; //хранение s показаний прибора

mn: real; // минимальное введенное число без s последних

m: real; //минимальное значение произведения

x: real; //очередное показание прибора

begin

readln(N); //количество показаний

//Ввод первых s чисел

for i:=1 to s do

readln(a[i]);

Задание Б. Способ 2 . Продолжение.

{ Ввод остальных значений, поиск минимального произведения}

mn := 1001; // минимальное введенное число без s последних

m := 1000 * 1000+1; // минимальное значение произведения

for i := s + 1 to N do begin

if a[1]

readln(x);

if x * mn

// сдвигаем элементы вспомогательного массива влево

for j := 1 to s - 1 do

a[j] := a[j + 1];

a[s] := x;

end;

writeln(m);

End.

Задание Б. Способ 3 на 4 балла. Алгоритм решения.

• Чтобы произведение было минимальным надо текущее значение умножать на минимальное из всех предшествующих, отстоящих от текущего на 6 и более показаний и выбирать из этих произведений минимальное.
• Каждое текущее минимальное показание используется после ввода ещё 6 элементов и после этого становится ненужным, поэтому достаточно хранить 6 последних минимумов. Для этого заведём массив armin[0..5]
• В каждом элементе массива будет хранится минимум подходящий для показаний, номер которых в потоке ввода равен номеру элемента массива armin по модулю 6.
• При поступлении очередного показания проверяем, не будет ли произведение текущего показания и записанного минимума наименьшим произведением и если это так, то обновляем Pmin
• Обновляем минимум (создаём минимум для показания с номером = текущий +6): берётся меньшее значение из текущего и записанного в массиве armin на предыдущем шаге.

Задание Б. Язык программирования PascalABC.net .

Const s = 6;

var armin: array[0..s-1] of real;

N, i : longint; a, Pmin : real;

Begin Readln(N);

//вводим первые s показаний и фиксируем минимумы

Readln(armin[1]);

for i:=2 to s do begin

readln(a);

armin[i mod s] := min(a, armin[i-1]);

end;

Pmin := 1000*1000+1; // ищем минимальное произведение

for i := s+1 to N do begin

readln(a);

Pmin := min(Pmin, a*armin[i mod s]);

armin[i mod s] := min(a, armin[(i-1) mod s])

end;

writeln(Pmin); end.

Задача 7. (ИНФ_ДЕМО 2016)

В физической лаборатории проводится долговременный эксперимент по изучению гравитационного поля Земли. По каналу связи каждую минуту в лабораторию передаётся положительное целое число – текущее показание прибора «Сигма 2015». Количество передаваемых чисел в серии известно и может быть очень велико (не превышает 10 000). Все числа не превышают 1000. Временем, в течение которого происходит передача, можно пренебречь. Необходимо вычислить «бета-значение» серии показаний прибора – минимальное чётное произведение двух показаний, между моментами передачи которых прошло не менее 6 минут. Если получить такое произведение не удаётся, ответ считается равным –1.

Демо 2016

6. В каждой из следующих N строк задаётся одно положительное целое число – очередное показание прибора. Пример входных данных: 11 12 45 5 3 17 23 21 20 19 18 17 Программа должна вывести одно число – описанное в условии произведение либо –1, если получить такое произведение не удаётся. Выходные данные для приведённого выше примера входных данных: 54 " width="640"

Входные данные представлены следующим образом. В первой строке задаётся число N – общее количество показаний прибора. Гарантируется, что N 6. В каждой из следующих N строк задаётся одно положительное целое число – очередное показание прибора.

Пример входных данных:

11

12

45

5

3

17

23

21

20

19

18

17

Программа должна вывести одно число – описанное в условии произведение либо –1, если получить такое произведение не удаётся.

Выходные данные для приведённого выше примера входных данных: 54

Подсказка № 1.

Чтобы произведение было чётным, хотя бы один сомножитель должен быть чётным, поэтому при поиске подходящих произведений чётные показания прибора можно рассматривать в паре с любыми другими, а нечётные – только с чётными.

Подсказка № 2.

Для каждого показания с номером k, начиная с k = 7, рассмотрите все допустимые по условиям задачи пары, в которых данное показание получено вторым.

Минимальное произведение из всех этих пар будет получено, если первым в паре будет взято минимальное подходящее показание среди всех, полученных от начала приёма и до показания с номером k – 6. Если очередное показание чётное, минимальное среди предыдущих может быть любым, если нечётное – только чётным .

Задание Б. Язык программирования PascalABC.

const amax = 1001 ; {больше максимально возможного показания}

var N: integer;

a: array[1..6] of integer ; {хранение 6 показаний прибора}

x: integer ; {ввод очередного показания}

ma: integer ; {минимальное число без 6 последних}

me: integer ; {минимальное чётное число без 6 последних}

mp: integer ; {минимальное значение произведения}

p: integer; i, j: integer;

begin

readln(N);

{Ввод первых 6 чисел}

for i:=1 to 6 do readln(a[i]);

{Ввод остальных значений, поиск минимального произведения}

ma := amax;

me := amax;

mp :=amax*amax;

for i := 7 to N do begin

readln(x);

if a[1]

if (a[1] mod 2 = 0) and (a[1]

if x mod 2 = 0 then p := x * ma

else p := x * me;

if (p

{сдвигаем элементы вспомогательного массива влево}

for j := 1 to 5 do a[j] := a[j + 1];

a[6] := x;

end;

if mp = amax*amax then mp:=-1;

writeln(mp);

end.

Задача 8. (ИНФ_ДЕМО 2019)

На вход программы поступает последовательность из N целых положительных чисел, все числа в последовательности различны. Рассматриваются все пары различных элементов последовательности, находящихся на расстоянии не меньше чем 4 (разница в индексах элементов пары должна быть 4 или более, порядок элементов в паре неважен). Необходимо определить количество таких пар, для которых произведение элементов делится на 29.

Описание входных и выходных данных

В первой строке входных данных задаётся количество чисел N (4 ≤ N ≤ 1000).

В каждой из последующих N строк записано одно целое положительное число, не превышающее 10 000.

В качестве результата программа должна вывести одно число: количество пар элементов, находящихся в последовательности на расстоянии не меньше чем 4, в которых произведение элементов кратно 29.

Демо 2016

Задача 8. Продолжение.

Пример входных данных:

7

58

2

3

5

4

1

29

Пример выходных данных для приведённого выше примера входных данных: 5

Пояснение. Из 7 заданных элементов с учётом допустимых расстояний между ними можно составить 6 произведений: 58·4, 58·1, 58·29, 2·1, 2·29, 3·29. Из них на 29 делятся 5 произведений.

Демо 2016

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А.
• Для подсчёта количества пар в которых произведение кратно 29 заводим переменную count и присваиваем ей начальное значение 0.
• В цикле перебираем все возможные пары и, если разница в индексах элементов пары 4 или более и их произведение кратно 29, увеличиваем count на 1.
• Выводим ответ, который подсчитан в count .

= 4) and (a[i]*a[j] mod 29 = 0) then count := count + 1; writeln(count); end. " width="640"

Задание А. Язык программирования PascalABC.

var N, i, j, count : integer;

a: array[1..10000] of integer;

begin

readln(N);

for i:=1 to N do

readln(a[i]);

count := 0;

for i:=1 to N-1 do

for j:=i+1 to N do

if (j-i = 4) and (a[i]*a[j] mod 29 = 0) then

count := count + 1;

writeln(count);

end.

Задание Б. Алгоритм решения .

• Произведение двух чисел делится на 29, если хотя бы один из сомножителей делится на 29.
• При вводе чисел можно подсчитывать количество чисел, кратных 29, не считая четырёх последних. Обозначим их n29.
• Очередное считанное число будем рассматривать как возможный правый элемент искомой пары.
• Если очередное считанное число делится на 29, то к ответу следует прибавить количество чисел до него, не считая четырёх последних. Если очередное считанное число на 29 не делится, то к ответу следует прибавить n29.
• Поскольку при обработке очередного элемента входных данных используются значения, находящиеся на четыре элемента ранее, достаточно хранить только четыре последних элемента.

Задание Б. Язык программирования PascalABC .

const s = 4; {требуемое расстояние между элементами}

var

N, i, j : integer;

x: integer; {очередное значение}

{хранение последних s значений}

a: array[1..s] of integer;

{количество делящихся на 29 элементов,

не считая s последних}

n29: integer ;

{количество искомых пар}

cnt: integer;

begin

readln(N);

{Ввод первых s чисел}

for i:=1 to s do readln(a[i]);

{Ввод остальных значений, подсчет искомых пар}

cnt := 0;

n29 := 0;

for i := s + 1 to n do begin

if a[1] mod 29 = 0 then

n29 := n29 + 1;

readln(x);

if x mod 29 = 0 then

cnt := cnt + i - s

else

cnt := cnt + n29;

{сдвигаем элементы вспомогательного массива влево}

for j := 1 to s - 1 do

a[j] := a[j + 1];

{записываем текущий элемент в конец массива}

a[s] := x

end;

writeln(cnt)

end.

Задача 9. (принесли дети в мае 2018 года)

На спутнике «Восход» установлен прибор, предназначенный для измерения солнечной активности. Каждую минуту прибор передаёт по каналу связи натуральное число – количество энергии солнечного излучения, полученной за последнюю минуту, измеренное в условных единицах. Временем, в течение которого происходит передача, можно пренебречь. Необходимо найти в заданной серии количество пар таких показаний прибора, произведение которых кратно 6 и между моментами передачи которых прошло не менее 3 минут . Количество энергии, получаемое прибором за минуту, не превышает 1000 условных единиц. Общее количество показаний прибора в серии не превышает 10 000.

Задача А (2 балла).  Напишите на любом языке программирования программу для решения поставленной задачи, в которой входные данные будут запоминаться в массиве, после чего будут проверены все возможные пары элементов.

Задача Б (4 балла).  Напишите программу для решения поставленной задачи, которая будет эффективна как по времени, так и по памяти (или хотя бы по одной из этих характеристик).

3. В каждой из следующих  N  строк задаётся одно натуральное число – очередное показание прибора. Пример входных данных: 5 6 2 4 1 3 Пример выходных данных для приведённого выше примера входных данных: 3 В приведённом наборе из 5 чисел имеются три пары (6, 3), (2, 3) и (6, 1), удовлетворяющих усло вию задачи. " width="640"

Задача 9. Продолжение.

Входные данные представлены следующим образом. В первой строке задаётся число  N  – общее количество показаний прибора. Гарантируется, что  N  3. В каждой из следующих  N  строк задаётся одно натуральное число – очередное показание прибора.

Пример входных данных:

5

6

2

4

1

3

Пример выходных данных для приведённого выше примера входных данных:

3

В приведённом наборе из 5 чисел имеются три пары (6, 3), (2, 3) и (6, 1), удовлетворяющих усло вию задачи.

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в массив А.
• Для подсчёта количества пар в которых произведение кратно 6 заводим переменную count и присваиваем ей начальное значение 0.
• В цикле перебираем все возможные пары и, если разница в индексах элементов пары 3 или более и их произведение кратно 6, увеличиваем count на 1.
• Выводим ответ, который подсчитан в count .

= 3) and (a[i]*a[j] mod 6 = 0) then count := count + 1; writeln(count); end. " width="640"

Задание А. Язык программирования PascalABC.

var N, i, j, count : integer;

a: array[1..10000] of integer;

begin

readln(N);

for i:=1 to N do

readln(a[i]);

count := 0;

for i:=1 to N-1 do

for j:=i+1 to N do

if (j-i = 3) and (a[i]*a[j] mod 6 = 0) then

count := count + 1;

writeln(count);

end.

Задание Б. Алгоритм решения .

• При вводе чисел можно подсчитывать количество чисел, не считая трёх последних, кратных 6, кратных 3, кратных 2 и не кратных 2, 3, 6. Обозначим их n6, n3, n2 и n1 соответственно.
• Очередное считанное число будем рассматривать как возможный правый элемент искомой пары.
• Для него корректируем счётчики n6, n3, n2 и n1 с учётом нового значения из очереди.
• Если очередное считанное число

• кратно 6, то оно образует пары со всеми числами;
• кратно 2, но не 3, то оно образует пары с числами, кратными 3;
• кратно 3, но не 2, то оно образует пары с числами, кратными 2;
• не кратно 2 и не кратно 3, образует пары с числами, кратными 6.

• Добавляем нужное количество в счётчик подходящих пар  k.
• После обработки всех значений выводим k.

Задание Б. Язык программирования PascalABC .

const s = 3; {требуемое расстояние между элементами}

var

N, i, j : integer;

x : integer; {очередное значение}

{хранение последних s значений}

a : array[0..s-1] of integer;

{количество чисел, кратных 6, кратных 3, кратных 2 и не кратных 2, 3, 6, не считая s последних}

n6, n3, n2, n1 : integer ;

k : integer; {количество искомых пар}

begin

readln(N);

{Ввод первых s чисел}

for i:=0 to s-1 do readln(a[i]);

{Ввод остальных значений, подсчет искомых пар}

uk := 0;

k := 0; n1 := 0; n2 := 0; n3 := 0; n6 := 0;

for i := s to n - 1 do begin

{обновляем счётчики}

if a[uk] mod 6 = 0 then n6 := n6 + 1

else if a[uk] mod 3 = 0 then n3 := n3 + 1

else if a[uk] mod 2 = 0 then n2 := n2 + 1

else n1 := n1 + 1;

{считываем очередное значение и обновляем k}

readln(x);

if x mod 6 = 0 then k := k + n1 + n2 + n3 + n6

else if x mod 3 = 0 then k := k + n2 + n6

else if x mod 2 = 0 then k := k + n3 + n6

else k := k + n6;

{записываем х в очередь и сдвигаем указатель}

A[uk] := x;

uk := (uk + 1) mod 3;

end ;

writeln(k) end.

Спасибо за внимание!

Вариации на тему Задачи 1

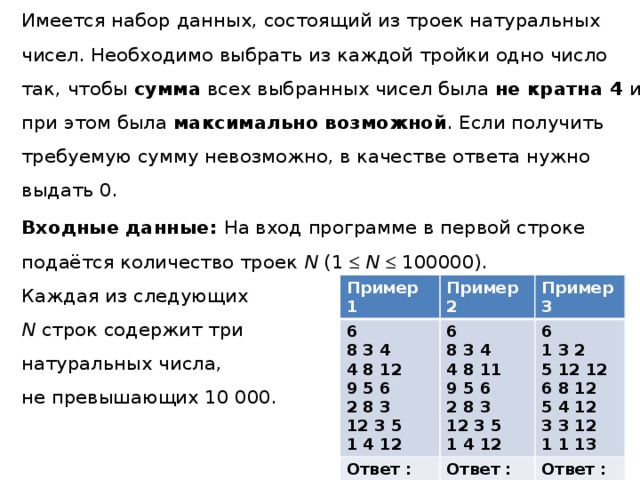
Имеется набор данных, состоящий из троек натуральных чисел. Необходимо выбрать из каждой тройки одно число так, чтобы сумма всех выбранных чисел была не кратна 4 и при этом была максимально возможной . Если получить требуемую сумму невозможно, в качестве ответа нужно выдать 0.

Входные данные: На вход программе в первой строке подаётся количество троек N (1  N  100000). Каждая из следующих N строк содержит три натуральных числа, не превышающих 10 000.

Пример 1

6

Пример 2

Пример 3

8 3 4

Ответ : 61

6

4 8 12

6

Ответ : 57

8 3 4

9 5 6

1 3 2

4 8 11

Ответ : 63

2 8 3

5 12 12

9 5 6

2 8 3

6 8 12

12 3 5

5 4 12

1 4 12

12 3 5

1 4 12

3 3 12

1 1 13

Взята у К.Ю. Полякова, задача № 73, автор Д.Ф. Муфаззалов. Для задания А (переборный вариант) оставляем 6 троек значений.

Задание A. Алгоритм решения.

• Сохраняем все исходные данные в двумерный массив А.
• Заведём переменную sMax для поиска максимального значения суммы и присвоим ей начальное значение 0.
• В цикле перебираем все возможные комбинации значений и считаем их сумму. Если очередная сумма оказывается больше sMax , обновляем sMax.
• Выводим ответ, который записан в sMax.

sMax) then sMax := s ; end; writeln(sMax); end. " width="640"

Задание А. Полный перебор.

var a: array[1..6, 1..3] of longint; s, sMax, i1, i2, i3, i4, i5, i6: longint;

Begin

for i1 := 1 to 6 do

readln(a[i1,1], a[i1,2], a[i1,3]);

sMax := 0 ;

for i1:=1 to 3 do

for i2:=1 to 3 do

for i3:=1 to 3 do

for i4:=1 to 3 do

for i5:=1 to 3 do

for i6:=1 to 3 do begin

s:=a[1,i1]+a[2,i2]+a[3,i3]+a[4,i4]+a[5,i5]+a[6,i6];

if (s mod 3 0) and (s sMax) then sMax := s ; end;

writeln(sMax);

end.

Задание Б. Алгоритм решения.

Если число кратно 4, то чтобы оно перестало быть кратным, из него нужно вычесть число, некратное 4.

Будем выбирать из каждой тройки наибольшее значение и найдем их сумму. Вместе с этим по всем тройкам будем искать наименьшую некратную 4 разницу между этим наибольшим значением и каждым из оставшихся чисел в тройке (*).

Если полученная сумма некратна 4, она и есть ответ. Если полученная сумма кратна 4, то если существует разница (*), вычтем ее из суммы, и это будет ответ, иначе выведем 0.

y) then min4:=y else min4:=x else if (x mod 4 = 0) and (y mod 4 = 0) then min4:= aMax + 1 else if (x mod 4 0) then min4:=x else min4:=y; end; " width="640"

Задание Б. Язык программирования PascalABC .

сonst aMax = 10000; //наибольшее возможное число в исходных данных

Var N, i : longint; //количество пар, переменная цикла

a, b, с : longint; //тройка чисел

S : longint; //сумма выбранных чисел

d : longint; //минимум в паре разностей с максимальным, не кратный 4

d_min : longint; //минимальная разница не кратная 4

function min4 (x, y : longint) : longint; // возвращает // наименьшее некратное 4 значение из х и у, если такого нет, то aMax + 1

begin

If (x mod 4 0) and (y mod 4 0) then

if (x y) then min4:=y else min4:=x

else if (x mod 4 = 0) and (y mod 4 = 0) then

min4:= aMax + 1

else if (x mod 4 0) then min4:=x else min4:=y;

end;

= b) and (a = c) then // a - максимум begin s := s + a; d := min4(a-b, a-c) end else if (b = a) and (b = c) then // b - максимум begin s := s + b; d := min4(b-a, b-c) end else // c - максимум begin s := s + c; d := min4(c-a, c-b) end; if d end; If (s mod 4 = 0) then If (d_min aMax) then s:= 0 else s:= s – d_min; writeln(s); end. " width="640"

begin

s := 0;

d_min := aMax + 1;

readln(N);

for i := 1 to N do begin

readln(a, b, c);

if (a = b) and (a = c) then // a - максимум

begin s := s + a; d := min4(a-b, a-c) end

else if (b = a) and (b = c) then // b - максимум

begin s := s + b; d := min4(b-a, b-c) end

else // c - максимум

begin s := s + c; d := min4(c-a, c-b) end;

if d

end;

If (s mod 4 = 0) then

If (d_min aMax) then s:= 0 else s:= s – d_min;

writeln(s);

end.

Что изменится в алгоритме, если надо найти максимальную сумму, кратную 4?

Надо найти три минимальные разности, которые при делении на 4 дают остатки 1, 2, 3. Тогда ответом будет :

сумма S если она кратна 4, или S – разность, соответствующая (S mod 4), если такая существует,

или 0.

Взята у К.Ю. Полякова, задача № 74, автор Д.Ф. Муфаззалов

Что изменится в программе, если надо найти максимальную сумму, кратную 4?

Для хранения минимальных разностей, которые при делении на 4 дают остатки 1, 2, 3 заведём глобальный массив d_min из трёх элементов с индексами 1, 2, 3, соответствующими остаткам от деления на 4.

Тогда ответом будет сумма S если она кратна 4,

или S – разность, соответствующая (S mod 4), если такая существует или 0.

0) and (x d_min[ost_x]:= x; If (ost_y 0) and (y d_min[ost_y]:= y; end; " width="640"

Задание Б. Язык программирования PascalABC .

сonst aMax = 10000 ; // наибольшее возможное число в исходных данных

Var N, i : longint; //количество пар, переменная цикла

a, b, с : longint ; //тройка чисел

S : longint; //сумма выбранных чисел

d_min : array[1..3] of longint; //минимальная разница не кратная 4

procedure min4 (x, y : longint);

var ost_x, ost_y : byte;

begin

ost_x := x mod 4; ost_y := y mod 4;

If (ost_x 0) and (x

d_min[ost_x]:= x;

If (ost_y 0) and (y

d_min[ost_y]:= y;

end;

= b) and (a = c) then // a - максимум begin s := s + a; min4(a-b, a-c) end else if (b = a) and (b = c) then // b - максимум begin s := s + b; min4(b-a, b-c) end else // c - максимум begin s := s + c; min4(c-a, c-b) end; end; If (s mod 4 0) then If (d_min[s mod 4] aMax ) then s := 0 else s := s - d_min[s mod 4] ; writeln(s); end. " width="640"

begin

s := 0;

for i := 1 to 3 do d_min[i] := aMax + 1;

readln(N);

for i := 1 to N do begin

readln(a, b, c);

if (a = b) and (a = c) then // a - максимум

begin s := s + a; min4(a-b, a-c) end

else if (b = a) and (b = c) then // b - максимум

begin s := s + b; min4(b-a, b-c) end

else // c - максимум

begin s := s + c; min4(c-a, c-b) end;

end;

If (s mod 4 0) then

If (d_min[s mod 4] aMax ) then s := 0

else s := s - d_min[s mod 4] ;

writeln(s);

end.

Что изменится в алгоритме, если надо найти максимальную сумму, кратную 4, но в тройке чисел выбирать два числа?

Алгоритм подсчёта суммы: в тройке чисел будем искать минимальное значение и прибавлять в сумму два больших.

Для сохранения минимальных разностей отправляем в процедуру min4 разности двух больших чисел с меньшим, например, если а – минимум, то отправим (в-а) и (с-а ).

0) and (x d_min[ost_x]:= x; If (ost_y 0) and (y d_min[ost_y]:= y; end; " width="640"

Задание Б. Язык программирования PascalABC.

сonst aMax = 10000; //наибольшее возможное число в исх. данных

Var N, i : longint; //количество пар, переменная цикла

a, b, с : longint; //тройка чисел

S : longint; //сумма выбранных чисел

//минимальная разница не кратная 4

d_min : array[1..3] of longint;

procedure min4 (x, y : longint);

var ost_x, ost_y : byte;

begin

ost_x := x mod 4; ost_y := y mod 4;

If (ost_x 0) and (x

d_min[ost_x]:= x;

If (ost_y 0) and (y

d_min[ost_y]:= y;

end;

aMax) then s := 0 else s := s - d_min[s mod 4]; writeln(s); end. " width="640"

begin

s := 0;

for i := 1 to 3 do d_min[i] := aMax + 1;

readln(N);

for i := 1 to N do begin

readln(a, b, c);

if (a // a - минимум

begin s := s + b + c; min4(b-a, c-a) end

else if (b // b - минимум

begin s := s + a + c; min4(a-b, c-b) end

else // c - минимум

begin s := s + a + b; min4(a-c, b-c) end;

end;

If (s mod 4 0) then

If (d_min[s mod 4] aMax) then s := 0

else s := s - d_min[s mod 4];

writeln(s);

end.

К задаче 2

К началу презентации

Конец