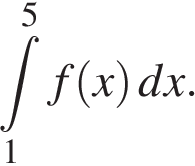ЕГЭ пробный профиль В2

Вариант № 26843044

1. Задание 1 № 26644

Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?

2. Задание 2 № 505160

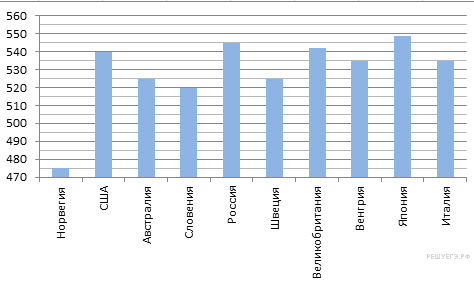
На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по естествознанию в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл участников выше, чем в Венгрии.

3. Задание 3 № 324465

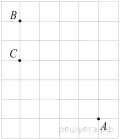На клетчатой бумаге с размером клетки 1×1 отмечены точки A, B и C. Найдите расстояние от точки A до прямой BC.

4. Задание 4 № 500037

Проводится жеребьёвка Лиги Чемпионов. На первом этапе жеребьёвки восемь команд, среди которых команда «Барселона», распределились случайным образом по восьми игровым группам — по одной команде в группу. Затем по этим же группам случайным образом распределяются еще восемь команд, среди которых команда «Зенит». Найдите вероятность того, что команды «Барселона» и «Зенит» окажутся в одной игровой группе.

5. Задание 5 № 282850

Найдите корень уравнения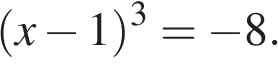 

6. Задание 6 № 27862

Найдите хорду, на которую опирается угол 120°, вписанный в окружность радиуса 

7. Задание 7 № 500890

На рисунке изображен график некоторой функции  Пользуясь рисунком, вычислите определенный интеграл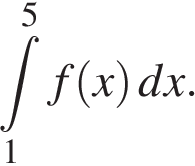 

8. Задание 8 № 509117

В правильной треугольной пирамиде боковое ребро равно 5, а тангенс угла между боковой гранью и плоскостью основания равен   Найти сторону основания пирамиды.

9. Задание 9 № 26823

Найдите  , если 

10. Задание 10 № 27958

Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна  , где   – масса воды в килограммах,   скорость движения ведeрка в м/с,   – длина верeвки в метрах, g – ускорение свободного падения (считайте   м/с ). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.

11. Задание 11 № 500253

Весной катер идёт против течения реки в   раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в   раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

12. Задание 12 № 77500

Найдите точку максимума функции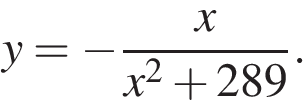 

13. Задание 13 № 507572

а) Решите уравнение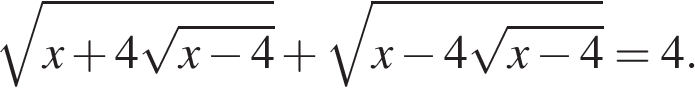 

б) Найдите решения уравнения, принадлежащие отрезку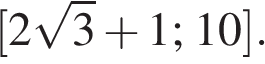 

14. Задание 14 № 509821

Основанием прямой четырехугольной призмы ABCDA'B'C'D' является квадрат ABCD со стороной  , высота призмы равна   Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.

а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

15. Задание 15 № 507893

Решите неравенство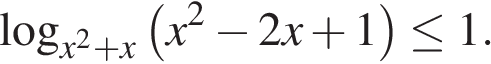 

16. Задание 16 № 514449

В треугольнике АВС проведены высоты АК и СМ. На них из точек М и К опущены перпендикуляры МЕ и КН соответственно.

а) Докажите, что прямые ЕН и АС параллельны;

б) Найдите отношение ЕН : АС, если угол АВС равен 30°.

17. Задание 17 № 510103

15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:

— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;

— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.

18. Задание 18 № 484632

При каких значениях параметра   система   имеет решения?

19. Задание 19 № 502079

Каждое из чисел a₁, a₂, …, a₃₅₀ равно 1, 2, 3 или 4. Обозначим

S₁ = a₁+a₂+...+a₃₅₀,

S₂ = a₁²+a₂²+...+a₃₅₀²,

S₃ = a₁³+a₂³+...+a₃₅₀³,

S₄ = a₁⁴+a₂⁴+...+a₃₅₀⁴.

Известно, что S₁ = 513.

а) Найдите S₄, если еще известно, что S₂ = 1097, S₃ = 3243.

б) Может ли S₄ = 4547 ?

в) Пусть S₄ = 4745. Найдите все значения, которые может принимать S₂.