Вариант № 26843046
1. Задание 1 № 318583
Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 37 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.
2. Задание 2 № 27511
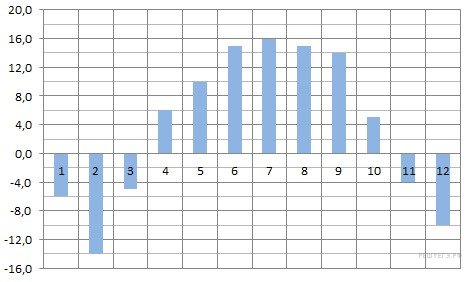
На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
3. Задание 3 № 27850
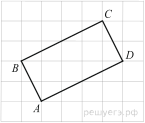 На клетчатой бумаге с размером клетки
На клетчатой бумаге с размером клетки 

 изображён четырёхугольник ABCD . Найдите его периметр.
изображён четырёхугольник ABCD . Найдите его периметр.
4. Задание 4 № 509011
Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами?
5. Задание 5 № 26660
Найдите корень уравнения 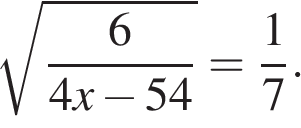
6. Задание 6 № 27239
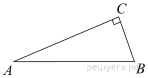 В треугольнике
В треугольнике 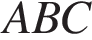 угол
угол 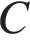 равен 90°,
равен 90°,  ,
, 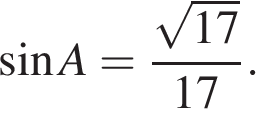 Найдите
Найдите 
7. Задание 7 № 323077
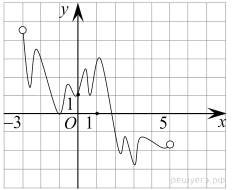
На рисунке изображён график функции y = F(x) — одной из первообразных функции f(x), определённой на интервале (−3; 5). Найдите количество решений уравнения f(x) = 0 на отрезке [−2; 4].
8. Задание 8 № 245344
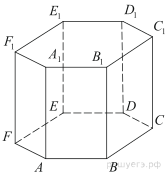 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки 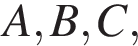
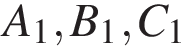 правильной шестиугольной призмы
правильной шестиугольной призмы 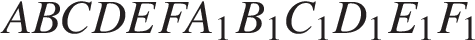 , площадь основания которой равна 6, а боковое ребро равно 3.
, площадь основания которой равна 6, а боковое ребро равно 3.
9. Задание 9 № 26783
Найдите значение выражения 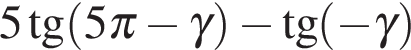 , если
, если 
10. Задание 10 № 324467
 На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке.
В этой системе координат линия, по которой провисает цепь моста, имеет уравнение 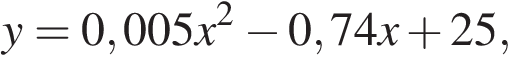 где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
11. Задание 11 № 323855
Клиент А. сделал вклад в банке в размере 7700 рублей. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Ровно через год на тех же условиях такой же вклад в том же банке сделал клиент Б. Еще ровно через год клиенты А. и Б. закрыли вклады и забрали все накопившиеся деньги. При этом клиент А. получил на 847 рублей больше клиента Б. Какой процент годовых начислял банк по этим вкладам?
12. Задание 12 № 77419
Найдите точку максимума функции 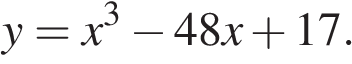
13. Задание 13 № 485991
а) Решите уравнение 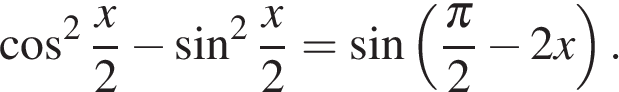
б) Укажите корни уравнения, принадлежащие отрезку 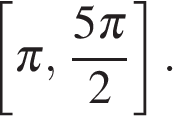
14. Задание 14 № 520496
В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.
а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.
б) Найдите площадь сечения пирамиды.
15. Задание 15 № 508255
Решите неравенство 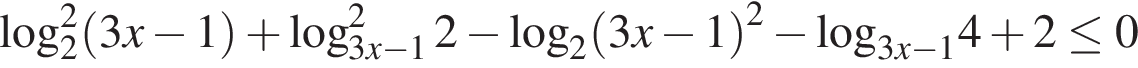
16. Задание 16 № 505568
Прямые, содержащие катеты AC и CB прямоугольного треугольника АСВ, являются общими внутренними касательными к окружностям радиусов 2 и 4. Прямая, содержащая гипотенузу АВ, является их общей внешней касательной.
а) Докажите, что длина отрезка внутренней касательной, проведенной из вершины острого угла треугольника до одной из окружностей, равна половине периметра треугольника АСВ.
б) Найдите площадь треугольника АСВ.
17. Задание 17 № 511283
В июле планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 31% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга, равную 69 690 821 рубль.
Сколько рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за три года)?
18. Задание 18 № 513278
Найдите все значения a, при каждом из которых модуль разности корней уравнения
принимает наибольшее значение.
19. Задание 19 № 505669
Можно ли из последовательности 1, 1/2, 1/3, 1/4,… выделить арифметическую прогрессию
а) длиной 4
б) длиной 5
в) длиной k, где k — любое натуральное число?








 На клетчатой бумаге с размером клетки
На клетчатой бумаге с размером клетки 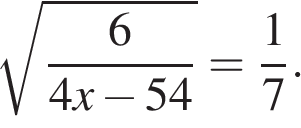
 В треугольнике
В треугольнике 
 Найдите объем многогранника, вершинами которого являются точки
Найдите объем многогранника, вершинами которого являются точки  На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.
На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами.









