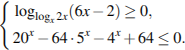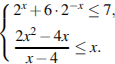Муниципальное бюджетное общеобразовательное учреждение
«Тальменская средняя общеобразовательная школа№5»
Тальменского района Алтайского края
| РАССМОТРЕНО Школьным методическим объединением ________________________ Руководитель ШМО Куприенко А.Ю. Протокол №1 от «28» 082023 г.
| СОГЛАСОВАНО Педагогическим советом учреждения Заместитель директора по УВР ________________________ Подболотова А.Г. Протокол №10 от «28» 08 2023 г.
| УТВЕРЖДЕНО Директор ________________________ Дериш К.А. Приказ №65-од от «28» 082023 г.
|
Рабочая программа элективного курса по математике для 11 класса
«Избранные вопросы математики»
на 2023 -2024 учебный год
Рабочая программа составлена на основе программы профильного образования
Издательство «Учитель» Волгоград 2009. Элективный курс Математика 10-11 классы Автор: Д.Ф.Айвазян.
Составитель Киряева Светлана Викторовна
учитель математики
высшей квалификационной категории
Тальменка 2022
Пояснительная записка
Рабочая программа учебного курса по выбору «Избранные вопросы математики » для класса составлена с учетом следующих нормативных документов и методических материалов:
приказа Минобрнауки Российской Федерации от 05.03.2009 №1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» (в ред. приказов Минобрнауки Российской Федерации от 03.06.2008 №164,от 31.08.2009 №320, от 19.10.2009№427, от 10.11 2011 №2643, от24.01.2012№39,от 31.01 2012 №69,от 23.06.2015№209, от7.06 т2017 №506)
приказа Минпросвещения России Российской Федерации от 23.12.2020 №766 « О федеральном перечне учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования»;
Приказ Минпросвещения России от 20 мая 2020 г. №254 «О внесении изменений в федеральный перечень учебников, рекомендуемых к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования, утвержденный приказом Министерства просвещений Российской Федерации от 23 декабря 2020 г. № 766»
приказа МКОУ Тальменская СОШ №5 от 13.11.2018 № 100 «Об утверждении основной образовательной программы среднего общего образования МКОУ Тальменская СОШ №5»;
приказа МБОУ Тальменская СОШ №5 от 28.08.2023 №65-од «Об утверждении Годового календарного учебного графика на 2023 – 2024 учебный год МБОУ Тальменская СОШ №5»;
приказа МБОУ Тальменская СОШ №5 от 28.08.2023 №65-од «Об утверждении Учебного плана на 2023- 2024 учебный год МБОУ Тальменская СОШ №5»;
приказа МБОУ Тальменская СОШ №5 от 28.08.2020 №56 «Об утверждении Положения о рабочей программе учебного предмета, курса МБОУ Тальменская СОШ №5»;
ЕГЭ по математике совмещает два экзамена – выпускной школьный и вступительный в ВУЗ. В связи с этим материал, усвоение которого проверяется при сдаче ЕГЭ, значительно шире материала, проверяемого при сдаче выпускного экзамена. Наряду с вопросами содержания школьного курса алгебры и начал анализа 10-11 классов проверяется усвоение ряда вопросов курсов алгебры 7-9 классов и геометрии 7-11 классов, которые традиционно контролируются на вступительных экзаменах. Таким образом, для подготовки к сдаче ЕГЭ необходимо повторить не только материал курса алгебры и начал анализа, но и некоторых разделов курса математики основной и средней школы: проценты, пропорции, прогрессии, материал курса планиметрии 7-9 классов и курса стереометрии 10-11 классов.
Данный курс предназначен для учащихся 11 класса и рассчитан на 68 часов. Разработка программы данного курса отвечает как требованиям стандарта математического образования, так и требованиям контрольно-измерительных материалов ЕГЭ. Программа составлена на принципе системного подхода к изучению математики. Она включает полностью содержание курса математики общеобразовательной школы, ряд дополнительных вопросов, непосредственно примыкающих к этому курсу, расширяющих и углубляющих его по основным идейным линиям, а также включены самостоятельные разделы. Такой подход определяет следующие тенденции:
1. Создание в совокупности с основными разделами курса для удовлетворения интересов и развития способностей учащихся.
2. Восполнение содержательных пробелов основного курса, придающее содержанию расширенного изучения необходимую целостность.
Программа предусматривает возможность изучения содержания курса с различной степенью полноты, обеспечивает прочное и сознательное овладение учащимися системой математических знаний и умений, достаточных для изучения сложных дисциплин и продолжения образования в высших учебных заведениях.
Цели курса: - практическая помощь учащимся в подготовке к Единому государственному экзамену по математике через повторение, систематизацию, расширение и углубление знаний;
- создание условий для дифференциации и индивидуализации обучения, выбора учащимися разных категорий индивидуальных образовательных траекторий в соответствии с их способностями, склонностями и потребностями;
- интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для жизни в современном обществе, для общей социальной ориентации и решения практических проблем.
Задачи курса:
- подготовить к успешной сдаче ЕГЭ по математике;
- активизировать познавательную деятельность учащихся;
- расширить знания и умения в решении различных математических задач, подробно рассмотрев возможные или более приемлемые методы их решения;
- формировать общие умения и навыки по решению задач: анализ содержания, поиск способа решения, составление и осуществление плана, проверка и анализ решения, исследование;
- привить учащимся основы экономической грамотности;
- повышать информационную и коммуникативную компетентность учащихся;
- помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
Курсу отводится 2 часа в неделю.
Всего 68 часов.
Особенности курса:
- интеграция разных тем;
- практическая значимость для учащихся.
Содержание курса:
Текстовые задачи 12 ч
Дроби и проценты. Смеси и сплавы. Движение. Работа. Задачи на анализ практической ситуации. Экономические задачи.
Выражения и преобразования 10 ч
Тождественные преобразования иррациональных и степенных выражений. Тождественные преобразования логарифмических выражений. Тождественные преобразования тригонометрических выражений.
Функции и их свойства 10 ч
Исследование функций элементарными методами. Производная функции, ее геометрический и физический смысл. Исследование функций с помощью производной.
Уравнения, неравенства и их системы 1 5 ч
Рациональные уравнения, неравенства и их системы. Иррациональные уравнения и их системы. Тригонометрические уравнения и их системы. Показательные уравнения, неравенства и их системы. Логарифмические уравнения, неравенства и их системы. Комбинированные уравнения и смешанные системы.
Планиметрия 8 ч
Треугольники. Четырехугольники. Окружность. Окружности, вписанные в треугольник и четырехугольник. Окружности, описанные около треугольника и четырехугольника.
Стереометрия 5 ч
Углы и расстояния. Сечения многогранников плоскостью. Площади поверхностей тел. Объемы тел.
Структура и содержание контрольно - измерительных материалов Единого государственного экзамена по математике 8 ч.
Требования к уровню подготовленности учащихся.
В результате изучения курса учащиеся должны уметь:
- вычислять значения корня, степени, логарифма;
- находить значения тригонометрических выражений;
- выполнять тождественные преобразования тригонометрических, иррациональных, показательных, логарифмических выражений;
- решать тригонометрические, иррациональные, показательные, логарифмические уравнения, неравенства, системы, включая с параметром и модулем, а также комбинирование типов аналитическими и функционально-графическими методами,
- строить графики элементарных функций, проводить преобразования графиков, используя изученные методы описывать свойства функций и уметь применять их при решении задач,
- применять аппарат математического анализа к решению задач;
- решать различные типы текстовых задач с практическим содержанием на проценты, движение, работу, концентрацию, смеси, сплавы, десятичную запись числа, на использование арифметической и геометрической прогрессии;
- уметь соотносить процент с соответствующей дробью;
-знать широту применения процентных вычислений в жизни, решать основные задачи на проценты, применять формулу сложных процентов;
- решать планиметрические задачи, связанные с нахождением площадей, линейных или угловых величин треугольников или четырехугольников;
- решать стереометрические задачи, содержащие разный уровень необходимых для решения обоснований и количество шагов в решении задач, включенных в часть I и часть II экзаменационной работы, часто требующие построения вспомогательных элементов и сечений, сопровождаемых необходимыми доказательствами;
- производить прикидку и оценку результатов вычислений;
- при вычислениях сочетать устные и письменные приемы, использовать приемы,
рационализирующие вычисления.
Виды деятельности на занятиях:
лекция учителя, беседа, практикум, консультация, ИКТ технологии, дистанционное обучение.
Формы контроля уровня достижений учащихся и критерии оценки
Текущий контроль: практическая работа, самостоятельная работа.
Тематический контроль: тест.
Итоговый контроль: итоговый тест.
Планируемые результаты
Изучение данного курса дает учащимся возможность:
- повторить и систематизировать ранее изученный материал школьного курса математики;
- освоить основные приемы решения задач;
- овладеть навыками построения и анализа предполагаемого решения поставленной задачи;
- овладеть и пользоваться на практике техникой сдачи теста;
- познакомиться и использовать на практике нестандартные методы решения задач;
- повысить уровень своей математической культуры, творческого развития, познавательной активности;
- познакомиться с возможностями использования электронных средств обучения, в том числе Интернет-ресурсов, в ходе подготовки к итоговой аттестации в форме ЕГЭ.
Учебно-методическое обеспечение
1. Гольдич В.А. Алгебра. Решение уравнений и неравенств. - СПб.: Литера, 2008
2. Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами. - М.-Харьков: "ИЛЕКСА", "Гимназия", 2009
3. Шарыгин И.Ф. Факультативный курс по математике. Решение задач – М. – «Просвещение» 2008
4. Кодификатор, спецификация заданий ЕГЭ 2013 -2014 г.
Интернет – источники:
Открытый банк задач ЕГЭ: http://mathege.ru
Он-лайн тесты:
http://uztest.ru/exam?idexam=25
http://egeru.ru
http://reshuege.ru/
5. ФИПИ http://fipi.ru/
6. МИОО http://www.mioo.ru/ogl.php#
7. http://shpargalkaege.ru/
Календарно -тематическое планирование курса(1.5часа в неделю, всего 51час).
| № | Тема | Кол. часов |
|
| 1. Текстовые задачи
| 12 |
| 1 2 | Задачи практического содержания (дроби, проценты). | 2 |
| 3 4 | Задачи практического содержания (смеси, сплавы). | 2 |
| 5 | Экономические задачи | 1 |
| 6 7 | Задачи на проценты | 2 |
| 8 | Задачи на движение | 1 |
| 9 | Задачи на работу и производительность | 1 |
| 10 | Задачи на прогрессии | 1 |
| 11 | Задачи на числа | 1 |
| 12 | Решение текстовых задач | 1 |
|
| 2. Выражения и преобразования. | 6 |
| 13 | Степени и корни | 1 |
| 14 | Тождественные преобразования иррациональных выражений | 1 |
| 15 | Тождественные преобразования степенных выражений | 1 |
| 16 | Преобразование тригонометрических выражений. | 1 |
| 17 | Тождественные преобразования логарифмических выражений. | 1 |
| 18 | Преобразование выражений. | 1 |
|
| 3. Функции и их свойства | 8 |
| 19 | Область определения функции, множество значений | 1 |
| 20 | Возрастание, убывание, экстремум функции | 1 |
| 21 | График функции | 1 |
| 22 | Исследование функций элементарными методами. | 1 |
| 23 | Производная, ее геометрический и физический смысл. | 1 |
| 24 | Исследование функции с помощью производной. | 1 |
| 25 | Первообразная функции | 1 |
| 26 | Площадь фигуры | 1 |
|
| 4. Уравнения, неравенства и их системы | 12 |
| 27 | Рациональные уравнения | 1 |
| 28 | Рациональные неравенства и их системы | 1 |
| 29 | Иррациональные уравнения | 1 |
| 30 | Системы иррациональных уравнений | 1 |
| 31 | Тригонометрические уравнения | 1 |
| 32 | Системы тригонометрических уравнений | 1 |
| 33 | Показательные уравнения | 1 |
| 34 | Показательные неравенства | 1 |
| 35 | Логарифмические уравнения | 1 |
| 36 | Логарифмические неравенства и системы | 1 |
| 37 | Комбинированные уравнения | 1 |
| 38 | Отбор корней уравнения | 1 |
|
| 5. Планиметрия | 5 |
| 39 | Треугольники. Четырехугольники | 1 |
| 40 | Окружности, вписанные в треугольник и четырехугольник. | 1 |
| 41 | Окружности, описанные около треугольника и четырехугольника | 1 |
| 42 | Решение комбинированных задач | 1 |
| 43 | Задачи на доказательство и вычисления | 1 |
|
| Стереометрия | 3 |
| 44 | Углы и расстояния. Сечения многогранников плоскостью. | 1 |
| 45 | Площади поверхностей объемы тел. | 1 |
| 46 | Решение стереометрических задач | 1 |
|
| Структура и содержание контрольно - измерительных материалов ЕГЭ | 5 |
| 47 | Система оценивания. Решение заданий с кратким ответом (задания 1-12). |
|
| 48 | Решение заданий с развернутым ответом ( задания 13-19). |
|
| 49 | Решение заданий с развернутым ответом |
|
| 50 | Тренировочные варианты ЕГЭ |
|
| 51 | Тренировочные варианты ЕГЭ. |
|
Приложение
Контрольно-измерительные материалы по курсу
Текстовые задачи
В университетскую библиотеку привезли новые учебники по геометрии для 2—3 курсов, по 280 штук для каждого курса. Все книги одинаковы по размеру. В книжном шкафу 7 полок, на каждой полке помещается 30 учебников. Сколько шкафов можно полностью заполнить новыми учебниками?
Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?
Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Ответ округлите до целого числа.
Для того, чтобы связать свитер, хозяйке нужно 800 граммов шерсти красного цвета. Можно купить красную пряжу по цене 80 рублей за 100 г, а можно купить неокрашенную пряжу по цене 50 рублей за 100 г и окрасить ее. Один пакетик краски стоит 20 рублей и рассчитан на окраску 400 г пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.
Для изготовления книжных полок требуется заказать 48 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25 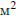 . В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
. В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена стекла (руб. за 1 м2) | Резка и шлифовка (руб. за одно стекло) |
| A | 420 | 75 |
| Б | 440 | 65 |
| В | 470 | 55 |
Независимая экспертная лаборатория определяет рейтинг 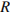 бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены
бытовых приборов на основе коэффициента ценности, равного 0,01 средней цены 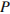 , показателей функциональности
, показателей функциональности 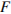 , качества
, качества 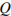 и дизайна
и дизайна 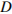 . Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле
. Каждый из показателей оценивается целым числом от 0 до 4. Итоговый рейтинг вычисляется по формуле
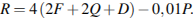 В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.
В таблице даны средняя цена и оценки каждого показателя для нескольких моделей электрических мясорубок. Определите наивысший рейтинг представленных в таблице моделей электрических мясорубок.
| Модель мясорубки | Средняя цена | Функциональность | Качество | Дизайн |
| А | 4600 | 2 | 0 | 2 |
| Б | 5500 | 4 | 3 | 1 |
| В | 4800 | 4 | 4 | 4 |
| Г | 4700 | 2 | 1 | 4 |
Четыре рубашки дешевле куртки на 8%. На сколько процентов пять рубашек дороже куртки?
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 110 литров она заполняет на 1 минуту быстрее, чем первая труба?
Решение.
Пусть 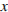 литров — объем воды, пропускаемой первой трубой в минуту, тогда вторая труба пропускает
литров — объем воды, пропускаемой первой трубой в минуту, тогда вторая труба пропускает 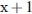 литров воды в минуту. Резервуар объемом 110 литров первая труба заполняет на 1 минуту дольше, чем вторая труба, отсюда имеем:
литров воды в минуту. Резервуар объемом 110 литров первая труба заполняет на 1 минуту дольше, чем вторая труба, отсюда имеем:
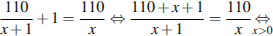
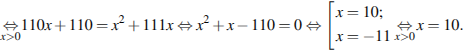
Значит, первая труба пропускает 10, а вторая — 11 литров воды в минуту.
Ответ: 11.
Ответ: 11
Тригонометрия
Решите уравнение 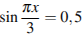 . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
Найдите 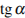 , если
, если 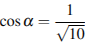 и
и 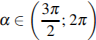 .
.
Найдите 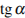 , если
, если 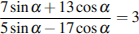
Найдите значение выражения 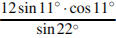
Найдите значение выражения 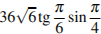 .
.
Найдите значение выражения 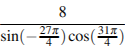
Найдите значение выражения 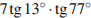 .
.
Найдите значение выражения 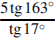
Найдите значение выражения 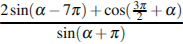
Дано уравнение 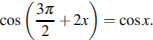 а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку
а) Решите уравнение; б) Укажите корни уравнения, принадлежащие отрезку 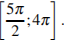
Планиметрия
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. 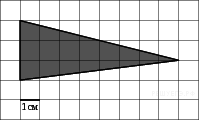
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 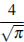 и
и 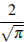 .
.
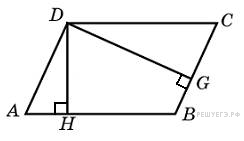
Стороны правильного треугольника 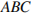 равны 3. Найдите скалярное произведение векторов
равны 3. Найдите скалярное произведение векторов 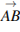 и
и 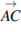 .
.
Точки O(0;, 0), A(6; 8), B(6; 2), C(0; 6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.
Решение.
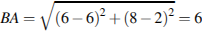 ,
,
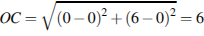 ,
,
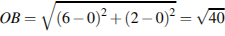 ,
,
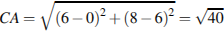 .
.
Противоположные стороны попарно равны, четырехугольник является параллелограммом, значит, точка P является серединой отрезка CB. Поэтому координаты точки P вычисляются следующим образом:
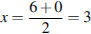 ,
, 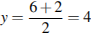 .
.
Ответ: 3.
Ответ: 3
8. В треугольнике 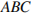
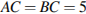 ,
, 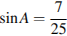 . Найдите
. Найдите 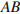 .
.
9. Четырехугольник 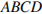 вписан в окружность. Угол
вписан в окружность. Угол 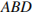 равен
равен 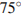 , угол
, угол 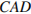 равен
равен 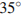 . Найдите угол
. Найдите угол 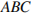 . Ответ дайте в градусах.
. Ответ дайте в градусах.
10. На прямой, содержащей медиану 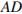 прямоугольного треугольника
прямоугольного треугольника 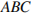 с прямым углом
с прямым углом  , взята точка
, взята точка 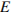 , удаленная от вершины
, удаленная от вершины 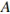 на расстояние, равное 4. Найдите площадь треугольника
на расстояние, равное 4. Найдите площадь треугольника 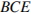 , если
, если 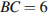 ,
, 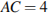 .
.
Стереометрия
В правильной треугольной пирамиде 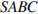 медианы основания
медианы основания 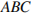 пересекаются в точке
пересекаются в точке  . Площадь треугольника
. Площадь треугольника 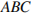 равна 2; объем пирамиды равен 6. Найдите длину отрезка
равна 2; объем пирамиды равен 6. Найдите длину отрезка 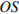 .
.
Найдите квадрат расстояния между вершинами C и A1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1=3.
Найдите расстояние между вершинами 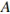 и
и 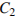 многогранника, изображенного на рисунке.
многогранника, изображенного на рисунке. 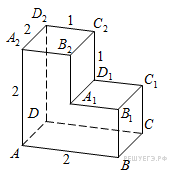 Решение.
Решение.
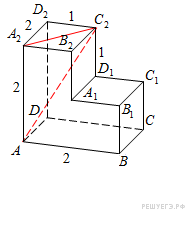 Рассмотрим прямоугольный треугольник, по теореме Пифагора
Рассмотрим прямоугольный треугольник, по теореме Пифагора 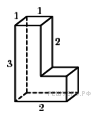
Найдите площадь поверхности многогранника, изображенного на рисунке
Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба. 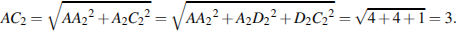 Ответ: 3.
Ответ: 3.
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10. Ответ: 3
Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.
Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.
В кубе 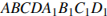 найдите косинус угла между плоскостями
найдите косинус угла между плоскостями 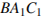 и
и 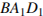 .
.
В прямоугольном параллелепипеде 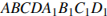 известны ребра:
известны ребра: 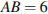 ,
,  ,
, 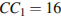 . Найдите угол между плоскостями ABC и
. Найдите угол между плоскостями ABC и 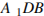 .
.
Производная
Материальная точка движется прямолинейно по закону 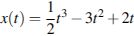 (где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
(где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения). Найдите ее скорость в (м/с) в момент времени t = 6 с.
Прямая  является касательной к графику функции
является касательной к графику функции 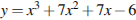 . Найдите абсциссу точки касания.
. Найдите абсциссу точки касания.
На рисунке изображен график функции y=f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
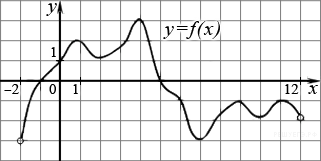
Найдите наименьшее значение функции 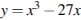 на отрезке
на отрезке 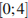 .
.
Найдите точку минимума функции 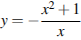 .
.
Найдите наименьшее значение функции 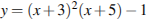 на отрезке
на отрезке 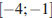 .
.
Найдите наибольшее значение функции 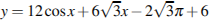 на отрезке
на отрезке 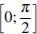
Найдите наименьшее значение функции 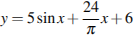 на отрезке
на отрезке 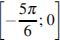 .
.
Найдите точку минимума функции 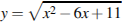 .
.
Найдите наибольшее значение функции 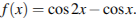
Вычисления и преобразования
Решите уравнение 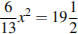 . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Найдите корень уравнения 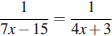
Найдите корень уравнения: 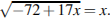 Если уравнение имеет более одного корня, укажите меньший из них.
Если уравнение имеет более одного корня, укажите меньший из них.
Найдите 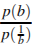 , если
, если 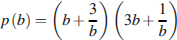 при
при 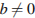 .
.
Найдите значение выражения 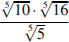
Найдите значение выражения 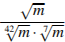 при
при 
Найдите значение выражения 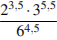 .
.
Найдите значение выражения 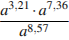 при
при  .
.
Найдите значение выражения 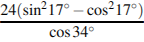
Найдите корни уравнения: 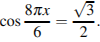 В ответе запишите наибольший отрицательный корень.
В ответе запишите наибольший отрицательный корень.
Практико – ориентированные задачи
При температуре 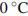 рельс имеет длину
рельс имеет длину 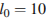 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону
м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону 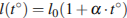 , где
, где 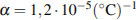 — коэффициент теплового расширения,
— коэффициент теплового расширения, 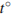 — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
— температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
По закону Ома для полной цепи сила тока, измеряемая в амперах, равна 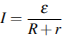 , где
, где 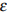 – ЭДС источника (в вольтах),
– ЭДС источника (в вольтах), 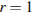 Ом – его внутреннее сопротивление,
Ом – его внутреннее сопротивление, 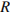 – сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более
– сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более  от силы тока короткого замыкания
от силы тока короткого замыкания 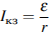 ? (Ответ выразите в Омах.)
? (Ответ выразите в Омах.)
Расстояние (в км) от наблюдателя, находящегося на высоте h м над землeй, выраженное в километрах, до наблюдаемой им линии горизонта вычисляется по формуле 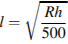 , где
, где 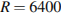 км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
км — радиус Земли. Человек, стоящий на пляже, видит горизонт на расстоянии 4,8 км. На сколько метров нужно подняться человеку, чтобы расстояние до горизонта увеличилось до 6,4 километров?
В ходе распада радиоактивного изотопа, его масса уменьшается по закону 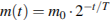 , где
, где 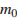 – начальная масса изотопа,
– начальная масса изотопа,  (мин) – прошедшее от начального момента время,
(мин) – прошедшее от начального момента время, 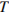 – период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени
– период полураспада в минутах. В лаборатории получили вещество, содержащее в начальный момент времени 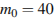 мг изотопа
мг изотопа 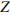 , период полураспада которого
, период полураспада которого  мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
мин. В течение скольких минут масса изотопа будет не меньше 5 мг?
Водолазный колокол, содержащий в начальный момент времени 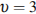 моля воздуха объeмом
моля воздуха объeмом 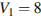 л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма
л, медленно опускают на дно водоeма. При этом происходит изотермическое сжатие воздуха до конечного объeма 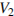 . Работа, совершаемая водой при сжатии воздуха, определяется выражением
. Работа, совершаемая водой при сжатии воздуха, определяется выражением 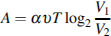 (Дж), где
(Дж), где 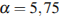 – постоянная, а
– постоянная, а  – температура воздуха. Какой объeм
– температура воздуха. Какой объeм 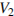 (в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?
(в литрах) станет занимать воздух, если при сжатии газа была совершена работа в 10350 Дж?
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности 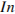 , оперативности
, оперативности 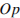 , объективности публикаций
, объективности публикаций 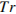 , а также качества сайта
, а также качества сайта 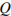 . Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
. Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5. Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид 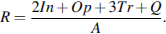 Каким должно быть число
Каким должно быть число 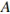 , чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
Мяч бросили под углом 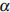 к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле
к плоской горизонтальной поверхности земли. Время полeта мяча (в секундах) определяется по формуле 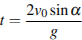 . При каком наименьшем значении угла
. При каком наименьшем значении угла 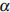 (в градусах) время полeта будет не меньше 3 секунд, если мяч бросают с начальной скоростью
(в градусах) время полeта будет не меньше 3 секунд, если мяч бросают с начальной скоростью 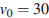 м/с? Считайте, что ускорение свободного падения
м/с? Считайте, что ускорение свободного падения 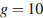 м/с
м/с .
.
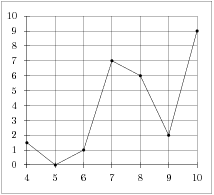 На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
В фирме такси в данный момент свободно 20 машин: 10 черных, 2 желтых и 8 зеленых. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчице. Найдите вероятность того, что к ней приедет зеленое такси.
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орёл выпадет ровно два раза.
Стереометрия
1.Высота конуса равна 6, а диаметр основания – 16. Найдите образующую конуса.
2. Площадь боковой поверхности цилиндра равна 21 , а диаметр основания равен 7. Найдите высоту цилиндра.
, а диаметр основания равен 7. Найдите высоту цилиндра.
3. Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 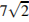 . Найдите радиус сферы.
. Найдите радиус сферы.
4. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.
5. Сосуд, имеющий форму правильной треугольной призмы, налили 2300 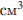 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в
воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в 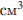 .
.
6. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.
7. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы.
8. Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 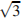 . 9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
. 9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.
Решение.
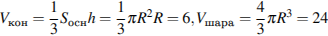 . .
. .
Ответ: 24.
Ответ: 24
10. В куб с ребром 3 вписан шар. Найдите объем этого шара, деленный на  .
.
Типовые задания С1, С2, С3, С4, С5, С6
C1 Решите уравнение 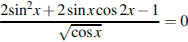 .
.
C1 а) Решите уравнение 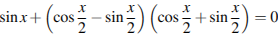 . б) Укажите корни этого уравнения, принадлежащие промежутку
. б) Укажите корни этого уравнения, принадлежащие промежутку 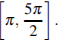
С 2 В правильном тетраэдре 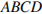 найдите угол между высотой тетраэдра
найдите угол между высотой тетраэдра 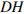 и медианой
и медианой 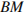 боковой грани
боковой грани  .
.
С 2 Дана правильная треугольная пирамида DABC с вершиной D. Сторона основания пирамиды равна 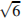 , высота равна
, высота равна 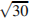 . Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно.
. Найдите расстояние от середины бокового ребра BD до прямой МТ, где точки М и Т — середины ребер АС и AВ соответственно.
С 3 Решите систему неравенств 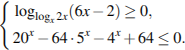
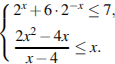
С 3 Решите систему неравенств
C4 Найдите длину отрезка общей касательной к двум окружностям, заключенного между точками касания, если радиусы окружностей раины 23 и 7, а расстояние между центрами окружностей равно 34.
Дан треугольник АВС. Точка Е на прямой АС выбрана так, что треугольник АВЕ, площадь которого равна 14, ― равнобедренный с основанием АЕ и высотой BD. Найдите площадь треугольника АВС, если известно, что 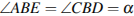 и
и 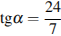 .
.
C5 Найдите все значения а, при каждом из которых множеством решений неравенства 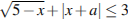 является отрезок.
является отрезок.
Найти все значения а, при каждом из которых функция 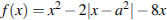 имеет более двух точек экстремума.
имеет более двух точек экстремума.
Перед каждым из чисел 14, 15, . . ., 20 и 4, 5, . . ., 8 прозвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Сумма двух натуральных чисел равна 43, а их наименьшее общее кратное в 120 раз больше их наибольшего общего делителя. Найдите эти числа.






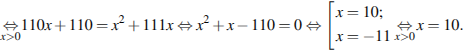


 Решение.
Решение. Рассмотрим прямоугольный треугольник, по теореме Пифагора
Рассмотрим прямоугольный треугольник, по теореме Пифагора 

 На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.
На рисунке изображен график осадков в Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм.