Элементы комбинаторики, теории множеств и математической логики

Элементы комбинаторики, теории множеств и математической логики

10/8/23

Домашнее задание.

Видеоурок Таблица истинности.

https :// www.youtube.com/watch?v=iynqE6QMuHw

Определение объема информации

1. Сколько различных цветов можно закодировать при помощи 6 бит информации?

Определение объема информации

2. В коробке 16 карандашей, все карандаши разного цвета. Какое количество информации получено в сообщении, что вытащен красный карандаш?

Определение объема информации

3. В корзине лежат 32 клубка шерсти, из них 4 красных. Сколько бит информации несет сообщение о том, что достали клубок красной шерсти?

• 2 3  4  32
• 2 3  4  32
• 2
• 3 
• 4 
• 32

Подумай

1) Сколько существует трёхзначных чисел?

2) Сколько способов проехать из  A  в  C , если система дорог такова, как показано на рисунке? 

КОМБИНАТОРИКА

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Самый простой метод решения комбинаторных задач – перебор всех возможных вариантов

1. Перечислить ВСЕ виды:

1) треугольников,

2) четырехугольников. Ответ:1) 6 2) 5

2. В магазине продают бейсболки трех цветов: синие, красные и черные. Ваня и Андрей покупают себе по одной. Сколько существует различных вариантов покупки? Ответ: 9 вариантов.

Перестановка

Имеется три овоща: свекла, морковь, баклажан. Сколькими способами можно их расположить на столе?

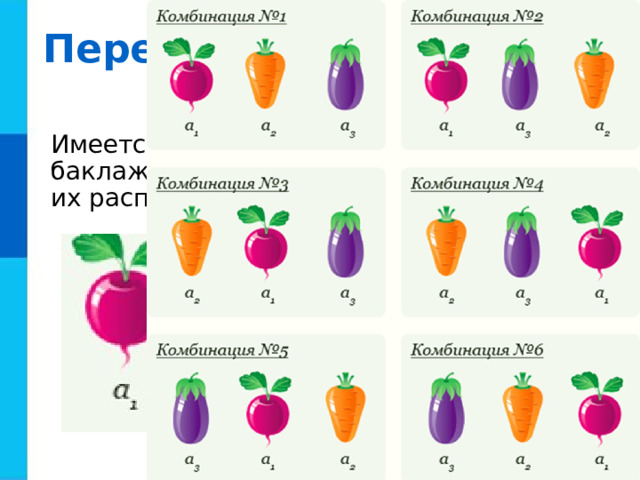
Перестановка

Имеется три овоща: свекла, морковь, баклажан. Сколькими способами можно их расположить на столе?

ФОРМУЛА ПЕРЕСТАНОВОК

Комбинации из n -элементов, отличающихся друг от друга только порядком расположения в них элементов, называются перестановками из n элементов.

Перестановки из n элементов обозначают P n и вычисляют по формуле: P n =n!

n!=1*2*3*4*…*n ( n факториал )

Примеры

• Сколькими способами можно расставить на полке 6 книг?

Примеры

• Сколькими способами можно расставить на полке 6 книг?

• … а если 10 книг?

3. Квартет

Проказница Мартышка

Осёл,

Козёл,

Да косолапый Мишка

Затеяли играть квартет

Что такое сочетание?

Сочетаниями из n элементов по m в каждом называются такие соединения, которые отличаются друг от друга хотя бы одним элементом.

• Обозначают:

Что такое сочетание?

Сочетание из n по m – это неупорядоченное множество, состоящее из m элементов, которые выбраны из n элементов.

Смысловая нагрузка:

«Сколькими способами можно выбрать m объектов их n?

0 m n

ПРИМЕР

• Сколько комбинаций чисел может составить игрок, играющий в лотереи « 5 из 36 », « 6 из 45 », « 7 из 49 »?

Вопрос 2: Сколькими способами можно выбрать

• а) один фрукт, б) два фрукта, в) три фрукта?

Решение.

• а) Один фрукт можно выбрать, очевидно, тремя способами – взять либо яблоко, либо грушу, либо банан. Формальный подсчёт проводится по формуле количества сочетаний (комбинаций):

Размещения

Размещением из n элементов по m ( m ≤ n ) называется любое множество, состоящее из любых m элементов, взятых в определенном порядке из данных n элементов.

Количество всех размещений из n элементов по m обозначают:

Размещение

• Есть три фрукта – груша, яблоко, банан. Сколькими способами можно раздать по одному фрукту Даше и Наташе?

Вопрос 3:

• Сколькими способами можно раздать по одному фрукту Даше и Наташе?
• Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно предыдущему вопросу, сделать это можно  3 способами: 1) яблоко и груша; 2) яблоко и банан; 3) груша и банан.
• Но комбинаций сейчас будет в два раза больше. Например, яблоком можно угостить Дашу, а грушей – Наташу; либо наоборот – груша достанется Даше, а  яблоко – Наташе. И такая перестановка возможна для каждой пары фруктов.
• В данном случае работает  формула количества размещений :

• Для того чтобы раздать два фрукта, сначала нужно их выбрать. Согласно предыдущему вопросу, сделать это можно  3 способами: 1) яблоко и груша; 2) яблоко и банан; 3) груша и банан.
• Но комбинаций сейчас будет в два раза больше. Например, яблоком можно угостить Дашу, а грушей – Наташу; либо наоборот – груша достанется Даше, а  яблоко – Наташе. И такая перестановка возможна для каждой пары фруктов.
• В данном случае работает формула количества размещений

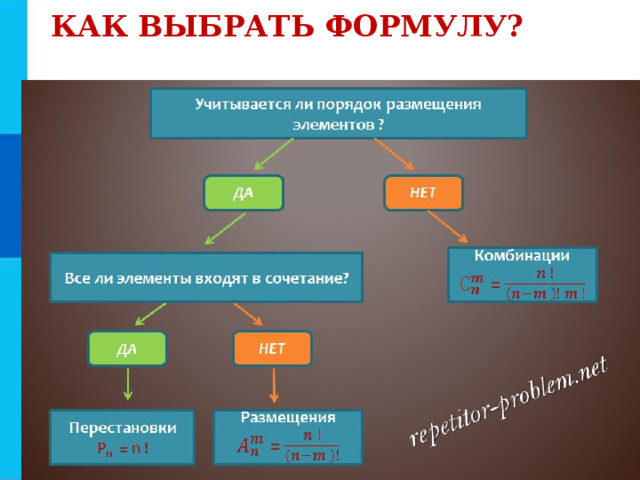
КАК ВЫБРАТЬ ФОРМУЛУ?

ЗАДАЧА

• Сколько разных трехзначных чисел можно записать с помощью цифр 1, 2, 3, 4, 5 при условии, что ни одна из цифр не повторяется?

РЕШЕНИЕ

• Для числа существенным является порядок записи цифр.

ЗАДАЧА

• Сколько разных цепочек длинной 3 можно записать из букв А, Б, В, Г, Д, Е при условии, что буквы могут повторяться?

РЕШЕНИЕ

• На первом месте можно записать любую из данных букв – всего 6 вариантов.
• Так как буквы могут повторяться, то на втором месте можно так же записать одну из 6 букв. 6*6=36 вариантов.
• Так же на третьем месте – одна из 6 букв:

ЗАДАЧА

• Необходимо выделить трех их пяти учеников на дежурство в столовую. Сколькими способами это можно сделать?

РЕШЕНИЕ

• При выборе учеников для дежурства порядок выбора несущественен. Нет разницы, в каком порядке учитель вызовет дежурных: «Петров, Иванов, Сидоров» или «Сидоров, Петров, Иванов». По сути это одна и та же тройка дежурных.

Логика. Логические операции

Логика является одной из дисциплин, образующих математический фундамент информатики .

Термин «логика» происходит от древнегреческого logos – «слово, мысль, понятие, рассуждение, закон».

Логика – это наука о законах и формах мышления. Она изучает абстрактное мышление как средство познания объективного мира.

3, H 2 O+SO 2 =H 2 SO 4 . " width="640"

Основным объектом в логике является высказывание .

Высказывание – это повествовательное предложение,

о котором можно сказать истинно оно или ложно.

Например,

предложение " 6 — четное число " - высказывание, т.к оно истинное.

Предложение " Рим — столица Франции « - высказывание, т.к. оно ложное.

Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например: 53, H 2 O+SO 2 =H 2 SO 4 .

3, H 2 O+SO 2 =H 2 SO 4 . " width="640"

Основным объектом в логике является высказывание .

Высказывание – это повествовательное предложение,

о котором можно сказать истинно оно или ложно.

Например,

предложение " 6 — четное число " - высказывание, т.к оно истинное.

Предложение " Рим — столица Франции « - высказывание, т.к. оно ложное.

Высказывания могут выражаться с помощью математических, физических, химических и прочих знаков. Например: 53, H 2 O+SO 2 =H 2 SO 4 .

Высказывание или нет?

• Сейчас идет дождь. Жирафы летят на север. История – интересный предмет. У квадрата – 10 сторон и все разные. Красиво! В городе N живут 2 миллиона человек. Который час?
• Сейчас идет дождь.
• Жирафы летят на север.
• История – интересный предмет.
• У квадрата – 10 сторон и все разные.
• Красиво!
• В городе N живут 2 миллиона человек.
• Который час?

Не всякое предложение является логическим высказыванием.

Например, предложения " ученик десятого класса " и " информатика — интересный предмет ". не являются высказываниями.

Вопросительные и восклицательные предложения также не являются высказываниями, т.к. в них ничего не утверждается и не отрицается.

Например :

1. Уходя, гасите свет! 2. Кто хочет быть счастливым?

Предложения типа " в городе A более миллиона жителей ", " у него голубые глаза " не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь. Такие предложения называются высказывательными формами

Примеры:

• Москва – столица России
• Студент математического факультета педагогического университета
• Треугольник АВС подобен треугольнику А’В’С’
• Луна есть спутник Марса
• Кислород – газ
• Каша – вкусное блюдо
• Математика – интересный предмет
• Железо тяжелее свинца
• Треугольник называется равносторонним, если все его стороны равны
• Сегодня плохая погода
• Река Ангара впадает в озеро Байкал

Высказывание

простое

составное

Высказывание называется простым ,

Высказывание называется составным ,

если никакая его часть сама

если оно состоит из простых высказываний,

не является высказыванием.

соединенных логическими связками:

И, ИЛИ, частицей НЕ

Обозначение высказываний

A – Сейчас идет дождь.

B – Форточка открыта.

простые высказывания (элементарные)

!

Любое высказывание может быть ложно (0) или истинно (1).

Составные высказывания строятся из простых с помощью логических связок (операций) « и» , « или» , « не» , « если … то» , « тогда и только тогда» и др.

Сейчас идет дождь и открыта форточка.

A и B

Сейчас идет дождь или форточка закрыта.

A или не B

Если сейчас идет дождь, то форточка открыта.

если A, то B

A тогда и только

Дождь идет тогда и только тогда, когда открыта форточка.

тогда, когда B

37

Начальный раздел математической логики называют алгеброй логики или Булевой алгеброй .

Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля .

Описал теорию логики и основу функционирования цифровых компьютеров в своей работе "Исследование законов мышления", 1854.

Простые высказывания обозначают

заглавными латинскими буквами

A, B, C…X, Y, Z и называют

логическими переменными

Значения высказываний

ИСТИНА или ЛОЖЬ обозначают

соответственно цифрами 1 и 0

и называют логическими величинами

Составные высказывания называются

логическими выражениями и включают

в себя логические переменные,

операции логики и скобки для изменения

порядка действий операций

3) B = (7 = 3) C = (7 ≠ 3) D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3)) На языке алгебры логики эти высказывания можно записать так: A = ИСТИНА = 1 B = ЛОЖЬ = 0 C = ИСТИНА = 1 D = ЛОЖЬ = 0 " width="640"

Примеры:

Рассмотрим следующие высказывания:

• A = (7 3)
• B = (7 = 3)
• C = (7 ≠ 3)
• D = (B ۸ C) = ((7 = 3) ۸ (7 ≠ 3))

На языке алгебры логики эти высказывания можно записать так:

A = ИСТИНА = 1

B = ЛОЖЬ = 0

C = ИСТИНА = 1

D = ЛОЖЬ = 0

Основные логические операции

Три базовых логических операций – инверсия, конъюнкция, дизъюнкция и дополнительные – импликация и эквиваленция (двойная импликация) .

37

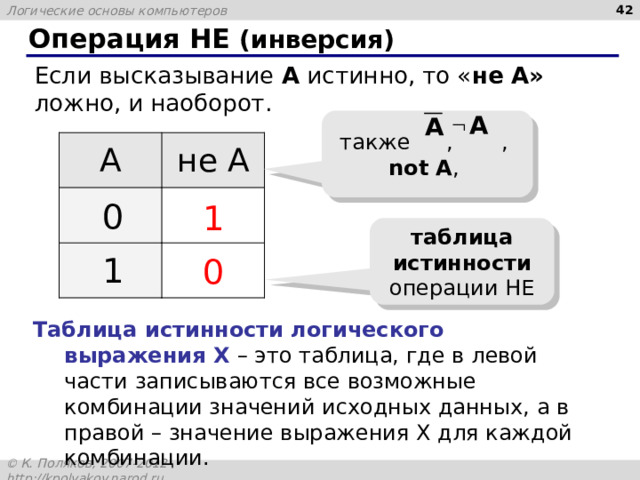
Операция НЕ (инверсия)

Если высказывание A истинно, то « не А» ложно, и наоборот.

также , , not A ,

А

не А

0

1

таблица истинности операции НЕ

1

0

Таблица истинности логического выражения Х – это таблица, где в левой части записываются все возможные комбинации значений исходных данных, а в правой – значение выражения Х для каждой комбинации.

3. 4 ≤ 5. Ответ: истинными высказываниями являются: 2 " width="640"

Примеры:

Сформулируйте отрицания следующих высказываний и укажите значения истинности полученных отрицаний:

• Волга впадает в Каспийское море.
• Число 28 не делится на число 7.
• 6 3.
• 4 ≤ 5.

Ответ: истинными высказываниями являются: 2

Операция И (логическое умножение, конъюнкция)

также: A·B , A  B , A and B , A & B

A

B

А и B

0

0

0

0

0

1

0

1

0

1

1

1

конъюнкция – от лат. conjunctio — соединение

44

Примеры:

Определить значения истинности следующих высказываний:

• Санкт - Петербург расположен на Неве и 2 + 3 = 5
• 7 – простое число и 9 – простое число
• 2 * 2 = 4 и 2 * 2 ≤ 5 и 2 * 2 ≥ 4
• Москва – столица России и Екатеринбург – столица Сибири
• Книга – источник информации и 5 не больше 8
• Девочки обычно любят играть в куклы и Не любая машина - автомобиль
• Все гуси – птицы и Все игрушки - машины

Ответ: истинными высказываниями являются: 1, 3, 5, 6

44

Операция ИЛИ (логическое сложение, дизъюнкция)

также: A+B , A  B , A or B , A || B

A

B

А или B

0

0

0

1

0

1

1

1

0

1

1

1

дизъюнкция – от лат. disjunctio — разъединение

46

Примеры:

Определить значения истинности следующих высказываний:

• 7 – простое число или 9 – простое число
• Число 2 четное и л и Это простое число
• 2 * 2 = 4 или Белые медведи живут в Африке
• Каша – вкусное блюдо или Математика – интересный предмет
• Луна – спутник Марса или Луна – спутник Земли
• Сегодня плохая погода или Кислород – вода
• Microsoft Word – текстовый редактор или Paint – графический редактор

Ответ: истинными высказываниями являются: 1, 2, 3, 5, 7

B , A B 0 А =B 0 0 1 1 1 1 1 0 0 1 1 Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно. Соответствует обороту ЕСЛИ…, ТО… " width="640"

46

Логическое операция ИМПЛИКАЦИЯ

также: A=B ,

A

B

0

А =B

0

0

1

1

1

1

1

0

0

1

1

Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся ложным тогда и только тогда, когда условие (первое высказывание) истинно, а следствие (второе высказывание) ложно.

Соответствует обороту ЕСЛИ…, ТО…

Примеры:

Определить значения истинности следующих высказываний:

• Если 12 делится на 6, то 12 делится на 3.
• Если 11 делится на 6, то 11 делится на 3.
• Если 15 делится на 6, то 15 делится на 3.
• Если 15 делится на 3, то 15 делится на 6.
• Если Саратов расположен на Неве, то белые медведи обитают в Африке.

Ответ: истинными высказываниями являются: 1, 2, 3, 5

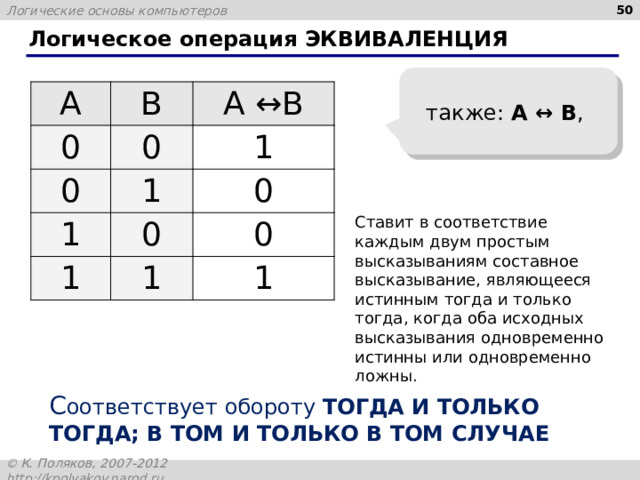
Логическое операция ЭКВИВАЛЕНЦИЯ

также: A ↔ B ,

A

B

0

А ↔B

0

0

1

1

1

1

0

0

0

1

1

Ставит в соответствие каждым двум простым высказываниям составное высказывание, являющееся истинным тогда и только тогда, когда оба исходных высказывания одновременно истинны или одновременно ложны.

С оответствует обороту ТОГДА И ТОЛЬКО ТОГДА; В ТОМ И ТОЛЬКО В ТОМ СЛУЧАЕ

Примеры:

Определить значения истинности следующих высказываний:

• 12 делится на 6 тогда и только тогда, когда 12 делится на 3.
• 11 делится на 6 тогда и только тогда, когда 11 делится на 3.
• 15 делится на 6 тогда и только тогда, когда 15 делится на 3.
• 15 делится на 5 тогда и только тогда, когда 15 делится на 4.

Ответ: истинными высказываниями являются: 1, 2

В А ۷ В А ↔ В 0 1 1 0 1 0 1 А 0 0 0 0 0 1 В 1 1 1 1 0 Ā 0 1 1 1 1 0 1 0 1 0 При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету: 1. инверсия, 2. конъюнкция, 3. дизъюнкция, 4. импликация и эквивалентность . " width="640"

Объединенная таблица истинности

А ۸ В

А = В

А ۷ В

А ↔ В

0

1

1

0

1

0

1

А

0

0

0

0

0

1

В

1

1

1

1

0

Ā

0

1

1

1

1

0

1

0

1

0

При вычислении значения логического выражения (формулы) логические операции вычисляются в определенном порядке, согласно их приоритету:

1. инверсия,

2. конъюнкция,

3. дизъюнкция,

4. импликация и эквивалентность .

Задачи

В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ | , а для логической операции «И» – &.

1) принтеры & сканеры & продажа

2) принтеры & продажа

3) принтеры | продажа

4) принтеры | сканеры | продажа

Примеры:

Логика и компьютер

Двоичное кодирование – все виды информации кодируются с помощью 0 и 1.

Задача – разработать оптимальные правила обработки таких данных.

Логика и компьютер

Почему «логика»? Результат выполнения операции можно представить как истинность (1) или ложность (0) некоторого высказывания.

Джордж Буль разработал основы алгебры, в которой используются только 0 и 1 (алгебра логики, булева алгебра).

Логические элементы ПК

В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например:

Логические элементы ПК

Логический элемент компьютера — это часть электронной логической схемы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И—НЕ, ИЛИ—НЕ и другие (называемые также вентилями ) .

Логические элементы ПК

Инвертор

1. Логический элемент «НЕ» (инвертор) реализует инверсию одного логического значения.

X

0

X

1

1

0

X

X

Коньюнктор

2. Логический элемент «И» (конъюнктор) реализует конъюнкцию двух или более логических значений.

X

0

Y

0

X&Y

0

0

1

1

1

0

0

0

1

1

X

&

X & Y

Y

Операция И

Высказывание « A и B» истинно тогда и только тогда, когда А и B истинны одновременно.

A и B

A

B

220 В

62

Дизъюнктор

3. Логический элемент «ИЛИ» (дизъюнктор) реализует дизъюнкцию двух или более логических значений.

X

0

Y

0

X+Y

0

0

1

1

1

1

0

1

1

1

X

1

X + Y

Y

Операция ИЛИ (логическое сложение, дизъюнкция)

Высказывание « A или B» истинно тогда, когда истинно А или B , или оба вместе.

A или B

B

A

220 В

64

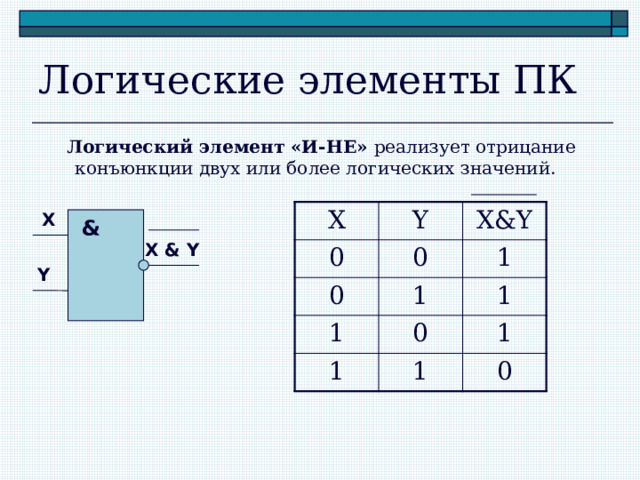
Логические элементы ПК

Логический элемент «И-НЕ» реализует отрицание конъюнкции двух или более логических значений.

X

0

Y

0

0

X&Y

1

1

1

1

1

0

1

1

0

X

&

X & Y

Y

Логические элементы ПК

Логический элемент «ИЛИ-НЕ» реализует отрицание дизъюнкции двух или более логических значений.

X

0

Y

0

0

X+Y

1

1

1

1

0

0

0

1

0

X

1

X + Y

Y

Логические элементы ПК

Задание №1: Записать логическую функцию, которую реализует следующая схема и таблицу истинности .

X

X

X & (Y+Z)

&

F=X & (Y + Z)

Y

1

Y+Z

Z

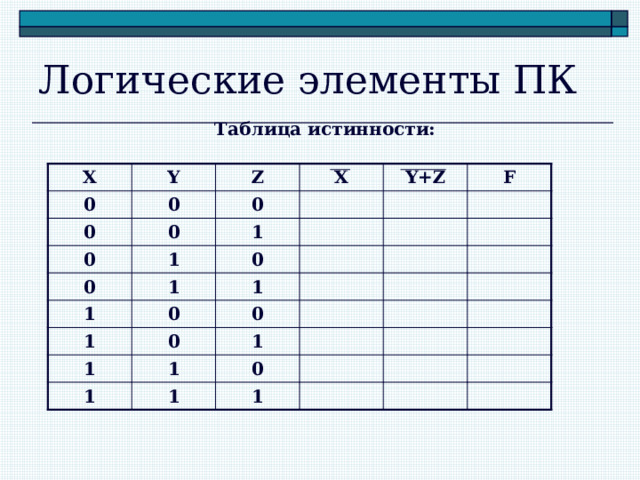
Логические элементы ПК

Таблица истинности:

X

Y

0

0

Z

0

X

0

0

0

1

0

Y+Z

1

0

1

F

1

0

1

1

0

0

1

1

1

1

0

1

1

1

&

1

А

F1

F2

V

В

1

0

F3

1

0

0

A & B v B

Структурная формула ЛУ

Функциональная схема логического устройства

Зная функциональную схему , можно составить данного ЛУ.

Анализир структурную формулу уя структурную формулу , можно создать функциональную схему и понять, как работает данное ЛУ.

Логические устройства ПК

P

A

B

S

Так как все многообразие операций в ПК сводится

к сложению двоичных чисел,

то главной частью процессора (АЛУ) является сумматор .

69

Рассмотрим сложение одноразрядных двоичных чисел :

Слагаемые

А

0

Перенос

В

Сумма

0

Р

0

1

1

0

S

0

0

1

0

1

0

1

1

1

0

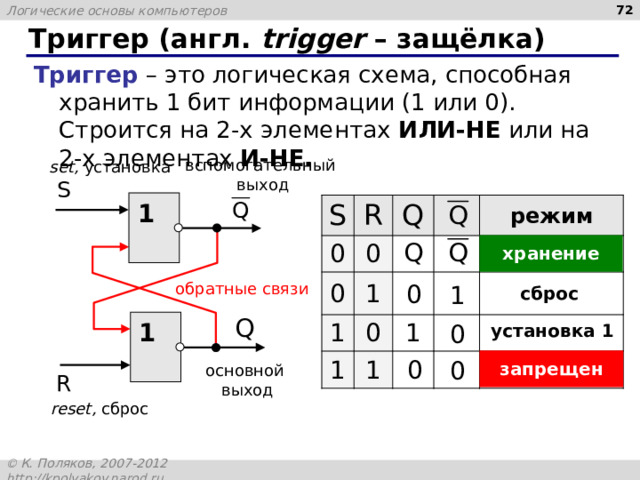
Триггер (англ. trigger – защёлка)

Триггер – это логическая схема, способная хранить 1 бит информации (1 или 0). Строится на 2-х элементах ИЛИ-НЕ или на 2-х элементах И-НЕ.

вспомогательный

выход

set, установка

1

S

R

0

0

0

Q

1

1

0

1

режим

1

хранение

обратные связи

0

сброс

1

установка 1

1

1

0

запрещен

0

0

основной

выход

reset, сброс

• Несколько триггеров можно объединить в группы - регистры

И использовать в качестве запоминающих устройств (ЗУ).

• Если в регистр входит N триггеров , то при таком ЗУ можно запоминать N-разрядные двоичные слова.

• ОЗУ ЭВМ часто конструируется в виде набора регистров.

• Один регистр образует одну ячейку памяти , каждая из которых имеет свой номер

1

т

0

1

т

1

1

0

т

1

1

т

Таким образом, ЭВМ

состоит из огромного числа

Отдельных логических элементов,

образующих все ее узлы и память.

Логические элементы ПК

Задание №2: Построить схему реализующую логическую

функцию

F=(A + B)&(A & B)

A

&

A & B

F 1 =A & B

B

A & B

&

F=(A + B)&(A & B)

1

A + B

Логические элементы ПК

Таблица истинности:

Домашнее задание: § 3.3, заполнить таблицы истинности.

A

0

B

0

0

A+B

1

1

A&B

0

A&B

1

F

1

Логические элементы компьютера

0 0

0

&

0

0 1

1

1 1

0

0 0

1

0 1

1

1

1 1

1 0

0 1

Логические схемы

&

1

&

&

С

В

А

F=X &(Y+Z)

X

F

&

Y+Z

1

Y

X

Z

Триггер

S

1

0

1

1

1

0

1

0

1

Q

R

Триггер

S

1

0

1

1

0

1

0

1

Q

R

Триггер

S

1

0

1

1

1

0

1

0

1

Q

R

Полусумматор

Cуммирование одноразрядных двоичных чисел без учета переноса из младшего разряда

Р

А

1

1

1

0

1

0

&

0

0

0

0

0

0

1

1

1

0

1

1

0

0

В

&

1

1

0

0

1

S

1

1

1

0

Одноразрядный двоичный сумматор

ai

bi

Pi

pi

Ci

A 0

A 1

A 2

В 2

В 1

В 0

0

С 0

С 1

С 2

С 3

А=(а 0+ а 1+ а 1 )

Результат А+В=С

А=(а 0+ а 1+ а 1 )

В=(в 0+ в 1+ в 1 )

С=(с 0+ с 1+ с 1 )

Задача: в звене 12 человек, требуется выбрать звеньевого, санитара и командира. Сколькими способами это можно сделать?

Решение:

Решение задач по теме «Перестановки »

1 .Курьер должен разнести пакеты в 7 различных учреждений. Сколько маршрутов он может выбрать?

2 .Сколькими способами 9 человек могут встать в очередь в театральную кассу?

3 .Ольга помнит, что телефон подруги оканчивается цифрами 5,7,8, но забыла, в каком порядке эти цифры следуют. Укажите наибольшее число вариантов, которые ей придётся перебрать, чтобы дозвониться подруге.

4.Сколько шестизначных чисел, в записи которых каждая цифра используется только один раз, можно составить из цифр: а)1,2,5,6,7,8; б)0,2,5,6,7,8?

5.Сколько существует перестановок букв слова «конус», в котором буквы «к», «о», «н» стоят рядом в указанном порядке?

Задачи по теме «Размещения»

1 Из 30 участников собрания надо выбрать председателя и секретаря. Сколькими способами это можно сделать?

2 На станции 7 запасных путей Сколькими способами можно расставить на них 4 поезда?

3 На странице альбома 6 свободных мест для фотографий. Сколькими способами можно вложить в свободные места: а) 2 фотографии; б) 4 фотографии; в) 6 фотографий?

4 Сколько четырёхзначных чисел, в которых нет одинаковых цифр, можно составить из цифр: а) 1, 3, 5, 7, 9,; б) 0, 2. 4, 6, 8?

5 Сколько существует семизначных телефонных номеров, в которых все цифры различные и первая цифра отлична от нуля?

• а) В конкурсе участвуют 8 школьников. Сколькими способами могут быть распределены места между ними? (Решение. 8! = 40 320).
• б) Сколькими способами можно составить маршрут путешествия, проходящего через 7 городов? (Решение. 7! = 5 040).
• в) Сколькими способами можно расставить на полке 10 различных книг? (Решение. 10! = 3 628 800).
• доп. № 619 ( представить, что всего 4 книги одного автора; подумать,сколькими способами можно их расставить; затем считать эти 4 книги одной книгой и добавить к ним оставшиеся книги; продолжить аналогичные рассуждения).
• Сколькими способами можно расставить на полке 10 книг, из которых 4 книги одного автора, а остальные – разных авторов, так, чобы книги одного автора стояли рядом? (Решение. 7! * 4!).