Автор –составитель :Паньковская Юлия Вадимовна
«Элементы комбинаторики»
ПРЕДИСЛОВИЕ
Представителям самых различных специальностей приходится решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов. Начальнику цеха надо распределить несколько видов работ между имеющимися станками, агроному – разместить посевы сельскохозяйственных культур на нескольких полях, заведующему учебной частью школы – составить расписание уроков, ученому-химику – рассмотреть возможные связи между атомами и молекулами, лингвисту – учесть различные варианты значений букв незнакомого языка и т.д. Область математики, в которой изучают закономерности создания подобных комбинаций, называется комбинаторикой.
Комбинаторика возникла в XVI веке. В то время в жизни общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр – вопросов, насколько часто можно выбросить данное число очков, бросая две или три кости, или получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и теории вероятностей.
Большим подспорьем для математиков являлось то, что решения задач такого рода можно было проверить на практике – во время игр. Зачастую проходило так, что во время многочасовых игр замечались определенные закономерности (например, что определенные комбинации карт или костей появляются чаще других), о которых игроки сообщали математикам, а последние объясняли эти наблюдения.
Одним из первых занялся подсчетом различного числа комбинаций при игре в кости итальянский математик Никколо Тарталья (ок.1499 -1557). Дальнейшее развитие комбинаторики связано с именами Блеза Паскаля (1623 – 1662), Пьера Ферма (1601 -1665), Якоба Бернулли (1654 -1705), Готфрида Вильгельма Лейбница (1646 -1716) и Леонарда Эйлера (1707 -1783). Однако у них основную роль играли приложения к различным играм (лото, солитер и др.), а также большое количество занимательных задач и головоломок. Долгое время казалось, что комбинаторика лежит вне основного русла развития математики и ее приложений.
Положение резко изменилось после появления во второй половине ХХ века электронных вычислительных машин и связанного с этим расцветом дискретной математики. С этого момента комбинаторика переживает период бурного развития. Комбинаторные методы находят множество применений. Они используются для решения транспортных задач (в частности задач по составлению расписаний), для составления планов производства и реализации продукции, в теории случайных процессов, статистике, вычислительной математике, планировании экспериментов, шахматных программах для ЭВМ и т.д. Комбинаторика используется для составления и декодирования шифров и для решения других проблем теории кодирования и теории информации. Значительную роль комбинаторные методы играют и в чисто математических вопросах – при изучении конечных геометрий, теории групп и их представлений, неассоциативных алгебр и т.д.
ОБЩИЕ ПРАВИЛА КОМБИНАТОРИКИ
«Суеверный председатель»
«Опять восьмерка!» - горестно воскликнул председатель клуба велосипедистов, взглянув на погнутое колесо своего велосипеда. «А все почему? Да потому, что у меня членский билет №088 – по восьмерке на каждое колесо! И теперь не проходит и месяца, чтобы то на одном, то на другом колесе не появилась восьмерка. Надо менять номер билета! А чтобы меня не обвинили в суеверии, проведу перерегистрацию всех членов клуба и буду выдавать только билеты с номерами, в которые ни одна восьмерка не входит. Не знаю только, хватит ли на всех номеров – ведь у нас в клубе почто 600 членов, а номера должны быть трехзначными. Неужели придется выписывать все номера от 000 до 999, а затем вычеркивать из них все номера с восьмерками?»
Попробуем помочь председателю. Нам нужно решить такую комбинаторную задачу: сколько трехзначных номеров, не содержащих цифры 8?
Для решения этой задачи определим сначала, сколько однозначных номеров не содержит цифру 8. Ясно, что таких номеров девять: 0, 1, 2, 3, 4, 5, 6, 7, 9. А теперь найдем все двузначные номера, не содержащие цифру 8. Их можно составить так: взять любой из найденных однозначных номеров и написать после него любую из девяти допустимых цифр. В результате из каждого однозначного номера получится девять двузначных. А так как однозначных номеров тоже девять, то получиться 9·9=92 двузначных номеров без цифры 8.
За каждым из них снова можно поставить любую из девяти допустимых цифр. В результате получим 92·9=93=729 трехзначных номеров, не содержащих цифру 8. Значит, таких членских билетов хватит на 729 членов клуба.
А если взять не трехзначные, а четырехзначные номера, то номеров, не содержащих цифру 8, будет 94=6561, а пятизначных – 95=59049.
Заместитель председателя был еще суевернее. Так как число 0 похоже на вытянутое колесо, он предложил отказаться и от этой цифры и попробовать обойтись восемью цифрами: 1, 2, 3, 4, 5, 6, 7, 9. А это у него получится, потому что эта задача похоже на решенную выше, только вместо девяти цифр у нас всего восемь. Поэтому и в ответе надо заменить 9 на 8, так что трехзначных номеров билетов, не использующих цифры 0 и 8, существует 83=512, а членов клуба почти 600.
«Лото»
Зоя Петровна и ее дочь Нина часто играли в лото. Каждая брала по три карточки, Нина хорошо перемешивала бочонки в мешке, затем доставала из мешка очередной бочонок с числом (от 1 до 90), называла его, и тот, у кого на карточке обнаруживалось это число, закрывал его бочонком.
Играли они часто, помнили, как начинались многие игры (кто первым и какой брал себе бочонок), уже не раз первым попадался один и тот же бочонок, но первые два бочонка каждый раз извлекались другие. И однажды Нина задумалась – много ли способов извлечь один за другим два бочонка из мешка, если в нем 90 бочонков?
Первый можно извлечь 90 способами – это понятно, а дальше? Ведь если бочонок 28 уже извлечен, то второй раз его извлечь нельзя. Но Нина как раз в это день готовила таблицу первенства школы по баскетболу, в которой клетки по диагонали перечеркивались (ведь играть сама с собой команда не может), и сообразила, что тот же метод годится и здесь. Она представила себе таблицу 90 90, в которой слева написаны возможные номера (от 1 до 90) бочонка, извлеченного первым, а сверху – возможные номера бочонка, извлеченного вторым.
90, в которой слева написаны возможные номера (от 1 до 90) бочонка, извлеченного первым, а сверху – возможные номера бочонка, извлеченного вторым.
Тогда каждая клетка задает один вариант выбора двух бочонков, вот только клетки диагонали надо зачеркнуть (дважды один бочонок извлечь нельзя).
В этой таблице 90·90=8100 клеток 90 зачеркнуты, значит, остается 8010 вариантов. Это и есть число способов извлечь один за другим два бочонка из 90.
А затем Нина сообразила, что можно рассуждать иначе. Первый бочонок можно извлечь 90 способами. После этого в мешке останется 89 бочонков, правда, каких – зависит от того, какой бочонок извлечен первым. Но способов извлечь второй бочонок всегда будет 89 для каждого из 90 способов извлечь первый бочонок, а всего способов будет 90·89=8010.
«Команда космического корабля»
В случае, когда число возможных выборов на каждом шагу сложным образом зависит от того, какие элементы были выбраны ранее, удобно изображать процесс составления комбинаций в виде «дерева». Сначала из данной точки проводят столько отрезков, сколько различных выборов можно сделать на первом шагу (таким образом, каждый отрезок соответствует одному элементу). Из конца каждого отрезка проводят столько отрезков, сколько можно сделать выборов на втором шагу, если в первый раз был выбран данный элемент, и т.д.
В результате такого построения получатся «дерево», рассмотрение которого дает число решений нашей задачи.
Рассмотрим следующий пример. Известно, что при составлении команд многоместных космических кораблей возникает вопрос о психологической совместимости участников космического путешествия. Даже вполне подходящие порознь люди могут оказаться непригодными для длительного совместного путешествия. Предположим, что надо составить команду космического корабля из трех человек: командира, инженера и врача. На место командира есть четыре кандидата: а1, а2, а3, а4; на место инженера – 3 кандидата: b1, b2, b3 и на место врача – тоже 3 кандидата: с1, с2, с3. Проведенная проверка показала, что командир а1 психологически совместим с инженерами b1 и b3 и врачами с2 и с3; командир а2 – с инженерами b1 и b2 и всеми врачами; командир а3 – с инженерами b1 и b2 и врачами с1, с3; командир а4 – со всеми инженерами и врачом с2. Кроме того, инженер b1 психологически несовместим с врачом с3, инженер b2 – с врачом с1 и инженер b3 – с врачом с2. Сколькими способами при этих условиях может быть составлена команда корабля?
Соответствующее дерево изображено на рис.1.
Оно показывает, что есть лишь 10 допустимых комбинаций. При этом после каждого выбора командира аi у нас есть 2 варианта выбора инженера bj, поэтому появляется 8 пар командир-инженер, а дальше для каждой такой пары в 6 случаях врач ck определен единственным образом (в силу требований совместимости), а в 2 случаях есть выбор из двух врачей.
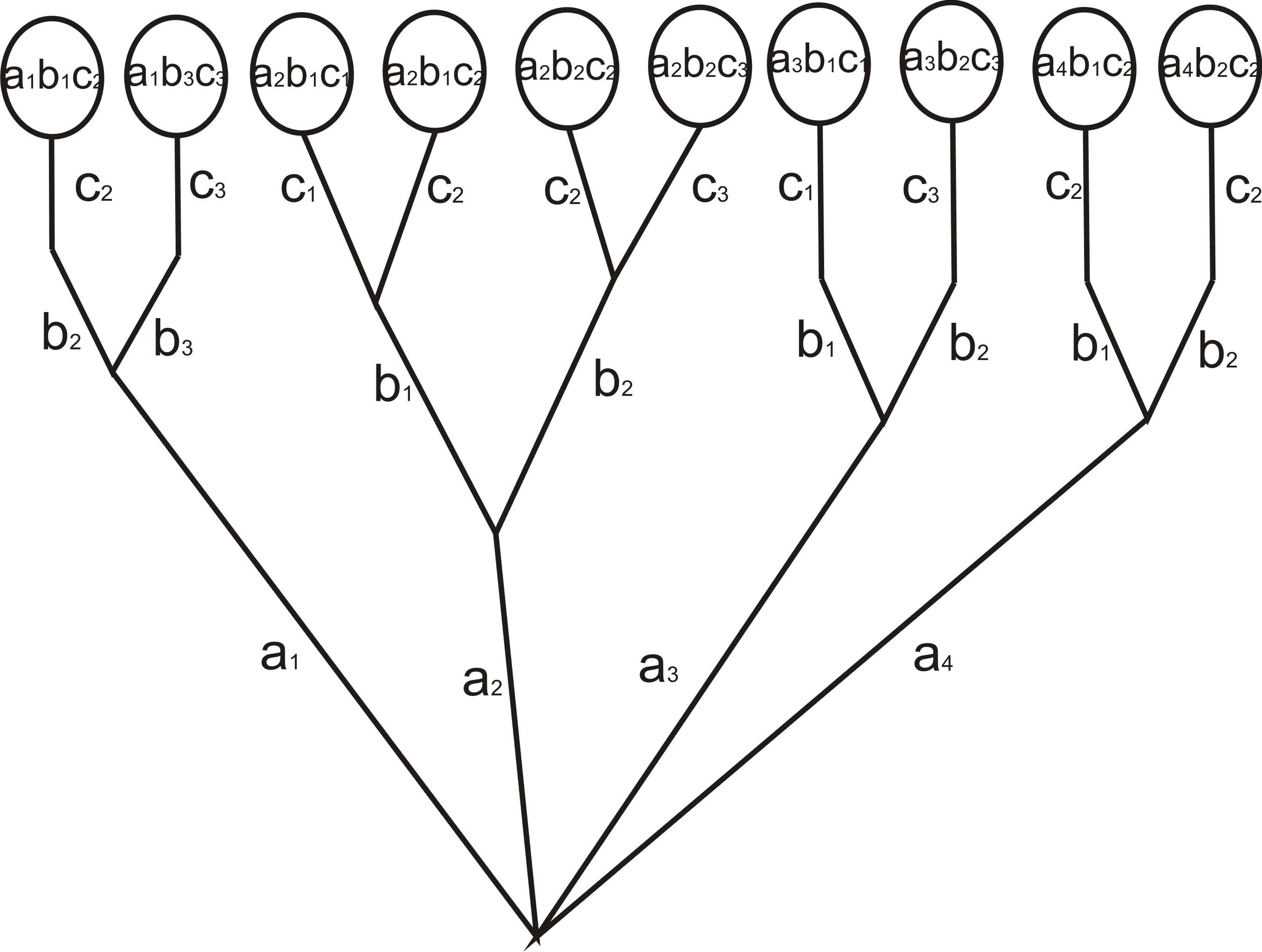 Если бы не было ограничения совместимости, то после каждого из 4 возможных способов выбора командира ai у нас было бы 3 варианта выбора инженера bj, а затем по 3 варианта выбора врача ck, и комбинаций было бы 4·3·3=36.
Если бы не было ограничения совместимости, то после каждого из 4 возможных способов выбора командира ai у нас было бы 3 варианта выбора инженера bj, а затем по 3 варианта выбора врача ck, и комбинаций было бы 4·3·3=36.
Задача 1. Крыса бежит по лабиринту, который устроен так, что сначала она должна выбрать одну из двух дверей, затем одну из трех дверей, а за каждой из них ее ожидают четыре двери. Пройдя какую-либо дверь, крыса не может вернуться через нее обратно. Сколькими различными путями крыса может пройти лабиринт?
Ответ: 2·3·4=24.
Задача 2. Сколькими способами можно прочитать слово КРОНА в таблице, начиная с буквы К в левом верхнем углу и двигаясь вправо или вниз до последней буквы?
| К | Р | О | Н | А |
| Р | О | Н | А | К |
| О | Н | А | К | Р |
| Н | А | К | Р | О |
| А | К | Р | О | Н |
Ответ: 24=16. На каждом шаге есть две возможности: идти направо или вниз.
Комбинаторные задачи бывают самых разных видов. Но многие решаются с помощью двух основных правил – правила суммы и правила произведения.
Правило суммы. Если на блюде лежат три яблока, то выбрать одно яблоко можно тремя способами (взять одно из трех яблок). Если на другом блюде лежат две груши, то выбрать одну грушу можно двумя способами (взять одну из двух груш). А выбрать один фрукт можно пятью способами (выбирая из пяти фруктов – трех яблок и двух груш). Это и есть правило суммы, которое можно сформулировать так.
Если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор «либо А, либо В» можно осуществить m+n способами.
Правило суммы применяют, когда удается разбить все изучаемые комбинации на несколько классов, причем каждая комбинация входит в один и только один класс. Ясно, что в этом общее количество комбинаций равно сумме количества комбинаций во всех классах.
Правило произведения. Это правило несколько сложнее, мы его уже фактически применяли в задачах о числе номеров билетов клуба велосипедистов и в задаче про лото.
Часто при составлении комбинации из двух элементов известно. Сколькими способами можно выбрать первый элемент, и сколькими способами второй, причем число способов выбора второго элемента не зависит от того, как именно выбран первый элемент. Пусть первый элемент можно выбрать m способами, а второй n способами. Тогда пару элементов можно выбрать mn способами. Иными словами:
Если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А; В) в указанном порядке можно осуществить mn способами.
Разумеется, может случиться, что нам надо составить не пары, а комбинации из большего числа элементов. Тогда мы приходим к следующей задаче.
Необходимо последовательно выбрать k элементов. Первым можно выбрать элемент а1 одного из n1 различных видов, вторым – элемент а2 одного из n2 различных видов, …, k-м – элемент аk из nk различных видов. При этом два способа выбора считаются различными, если хотя бы на одном месте в них стоят разные элементы. Сколькими способами можно произвести такой выбор?
Эта задача решается так же, как задача о клубе велосипедистов. Первый элемент можно выбрать n1 способами. Каждый из выбранных элементов а1 можно соединить с любым из n2 видов элементов а2, что дает n1n2 пар. Каждую такую пару можно соединить с любым из n3 видов элементов а3, что дает n1n2n3 троек. Продолжая далее, мы получим, в конце концов, n1n2n3…nk способов.
Так как для подсчета числа всевозможных способов приходится перемножать числа n1, n2, …,nk, то выведенный результат называют «правилом произведения».
Задача 3. В киоске продаются 5 видов конвертов и 4 вида марок. Сколькими способами можно купить пару из конверта и марки?
Ответ: 5·4=20.
Задача 4. В футбольной команде (11 человек) нужно выбрать капитана и его заместителя. Сколько комбинаций возможно?
Ответ: 11·10=110.
Задача 5. Сколькими способами можно выбрать гласную и согласную буквы из слова КОНВЕРТ?
Ответ: 2·5=10.
Задача 6. Сколькими способами можно поставить на шахматную доску две ладьи так, чтобы они не били друг друга?
Ответ: 64·49=3136.
Задача 7. На каникулы школьник получил задание: выучить доказательство любой из шести теорем, прочитать один из семи романов, написать сочинение на одну из четырех тем. Сколько комбинаций домашнего задания можно составить?
Ответ: 6·7·4=168.
Задача 8. Сколькими способами из набора костей домино можно выбрать две кости так, чтобы их можно было приложить друг к другу (т.е. чтобы какое-то число очков встречалось бы на обеих костях)?
Решение. В 7 случаях выбранная кость окажется «дублем», т.е. костью вида 0-0, 1-1, 2-2, 3-3, 4-4, 5-5,6-6, а в 21=(7·6):2 случае – костью с различными числами очков. Сначала выберем одну кость. Это можно сделать 28 способами. В первом случае вторую кость можно выбрать 6 способами. Во втором же случае вторую кость можно выбрать 12 способами (для кости 3-5 подойдут кости как с числом 3, так и с числом 5). По правилу произведения в первом случае получаем 7·6 выбора, а во втором случае 21·12 выбора. Значит, по правилу суммы получаем 42+252=294 способа выбора пары.
Ответ: 294.
Задача 9. Сколькими способами можно поставить на шахматную доску белого и черного короля так, чтобы получилась допустимая правилами игры позиция?
Решение. Белого короля можно поставить на любое из 64 полей. Однако количество полей, которые он при этом будет бить, зависит от его расположения. Поэтому разберем три случая:
Если белый король стоит в углу (углов всего 4), то он бьет 3 поля, и остается 60 полей, на которые можно поставить черного короля;
Если белый король стоит на краю доски, но не в углу (таких полей -24), то он бьет 5 полей, и для черного короля остается 58 возможных полей;
Если же белый король стоит не на краю доски (таких полей – 36), то он бьет 8 полей, и для черного короля остается 55 возможных полей.
Таким образом, всего есть 4·60+24·58+36·55=3612 способов расстановки королей.
Ответ: 3612.
Задача 10. У англичан принято давать ребенку несколько имен. Сколькими способами в Англии можно назвать ребенка, если общее число имен равно 300, а ему дают не более четырех имен? Хватит ли этих наборов на всех англичан (около 51 млн чел.) или непременно найдутся англичане с одинаковыми именами?
Ответ: 300+300·299+300·299·298+300·299·298·297=7 965 808 800. На всех англичан хватит.
Задача 11. Сколько есть чисел от 0 до 999999, в которых нет двух рядом стоящих одинаковых цифр?
Ответ: 10+92+93+94+95+96=597871.
Задача 12. C 2004 года на Украине введены автомобильные номера, состоящие из четырех цифр и четырех букв – по две с каждой стороны (это код региона и серия номера) – АА1345АА. Найдите число таких номеров, если используются 12 букв, и нет номера с четырьмя нулями.
Ответ: 124·(104 -1)=20715264.
Задача 13. С 1993 года в России определены стандартные регистрационные знаки для автомобилей типа х451хо77. Комбинации на стандартных номерных знаках строятся по принципу — 3 буквы, 3 цифры. Буквы означают серию номерного знака, а цифры — номер. ГОСТом для использования на знаках разрешены 12 букв кириллицы, имеющие графические аналоги в латинском алфавите — А, В, Е, К, М, Н, О, Р, С, Т, У и Х. Две или три последние цифры –это код региона.
а) Сколько таких автомобильных номеров могли выдать в одном регионе России, если номера 000 не может быть?
б) на Москву были выделены коды региона 77, 97, 99, 177, 197 и 199. Сколько стандартных номеров может быть в Москве?
Ответ: а) (103 -1)·123=1726272,
б) (103 -1)·123·6=10357632.
Задача 14. Сколько чисел, меньших миллиона, можно написать с помощью цифр:
а) 8 и 9; б) 7, 8 и 9; в) 0, 8 и 9 (с цифры 0 число начинаться не может)?
Ответ: а) 21+22+23+24+25+26=126; б) 31+32+33+34+35+36=1092; в) 2(30+31+32+33+34+35)=728.
ПЕРЕСТАНОВКИ, РАЗМЕЩЕНИЯ И СОЧЕТАНИЯ
«Первенство по футболу»
В первенстве страны по футболу участвовали 16 команд. Перед началом первенства был объявлен конкурс знатоков, в котором требовалось предсказать распределение медалей. Сколько различных ответов можно дать на этот вопрос?
Эта задача решается на основе правила произведения. Комплект золотых медалей может получить любая из 16 команд. Но если золотые медали уже завоеваны какой-то командой, занявшей 1 место, то остается лишь 15 претендентов на второе место и серебряные медали. Повторения здесь быть не может – одна и та же команда не может завоевать и золотые, и серебряные медали.
Значит, после вручения чемпиону золотых медалей остается 15 возможностей получения серебряных медалей. Точно так же, если уже вручены и золотые, и серебряные медали, то на третье место и бронзовые медали претендует лишь одна из оставшихся 14 команд. По правилу произведения получаем, что медали могут быть распределены 16·15·14=3360 способами.
Данная задача относится к классу комбинаторных задач о размещения без повторений. Общая формулировка такова.
Имеется «бланк», в котором k мест: 1-е, 2-е, …, k-е. все места вакантны. Их надо заполнить элементами. Имеется запас из n различных элементов, и на каждое место можно поставить один из этих элементов, но теперь каждый элемент в единственном числе, поэтому элементы не могут повторяться. Сколько существует способов заполнить такой «бланк»? два способа заполнения считаются различными, если хотя бы на одном месте в них стоят разные элементы.
Каждый способ заполнения позволяет разместить на k местах некоторые из n элементов, причем элементы не могут повторяться, поэтому он называется размещением без повторений из n элементов по k. Число всех таких размещений обозначают 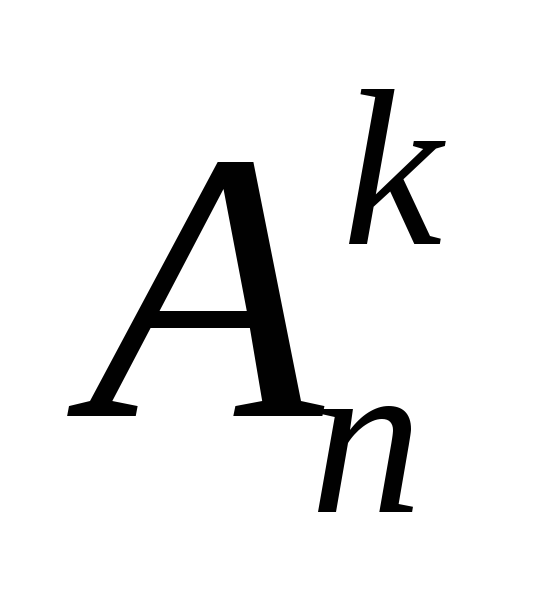 .
.
Чтобы сосчитать 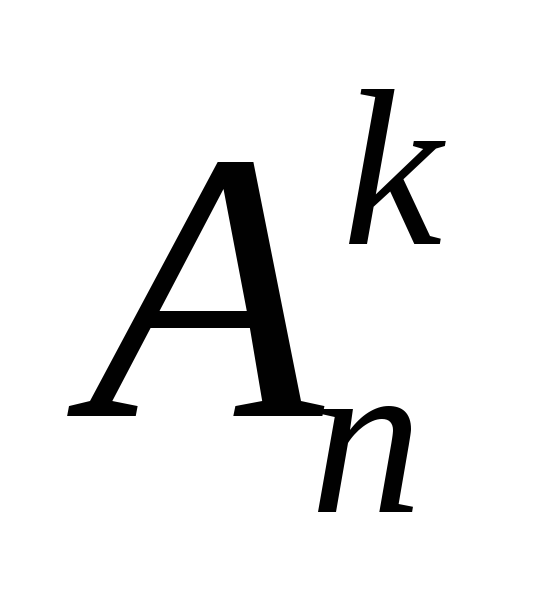 , будем рассуждать так. При составлении размещений без повторений из n элементов по k нам надо сделать k выборов. На первом шагу можно выбрать любой из имеющихся n элементов. Если этот выбор уже сделан, то на втором шагу приходится выбирать из оставшихся n-1 элементов. Точно также на третьем шагу для выбора остается запас лишь из n-2 элементов, на четвертом – из n-3 элементов, …, на k-ом шагу – из n-(k-1)=n-k+1 элементов. Применяя правило произведения, получаем, что число размещений без повторений из n элементов по k выражается следующим образом:
, будем рассуждать так. При составлении размещений без повторений из n элементов по k нам надо сделать k выборов. На первом шагу можно выбрать любой из имеющихся n элементов. Если этот выбор уже сделан, то на втором шагу приходится выбирать из оставшихся n-1 элементов. Точно также на третьем шагу для выбора остается запас лишь из n-2 элементов, на четвертом – из n-3 элементов, …, на k-ом шагу – из n-(k-1)=n-k+1 элементов. Применяя правило произведения, получаем, что число размещений без повторений из n элементов по k выражается следующим образом: 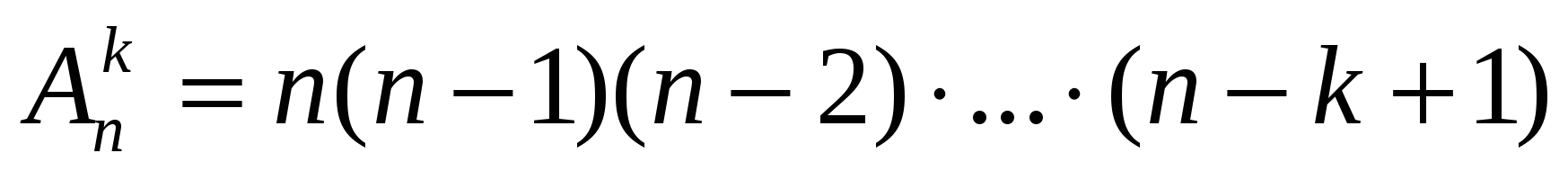 .
.
Эту формулу можно записать иначе, домножив числитель и знаменатель на произведение (n-k)(n-k-1)·…·1:
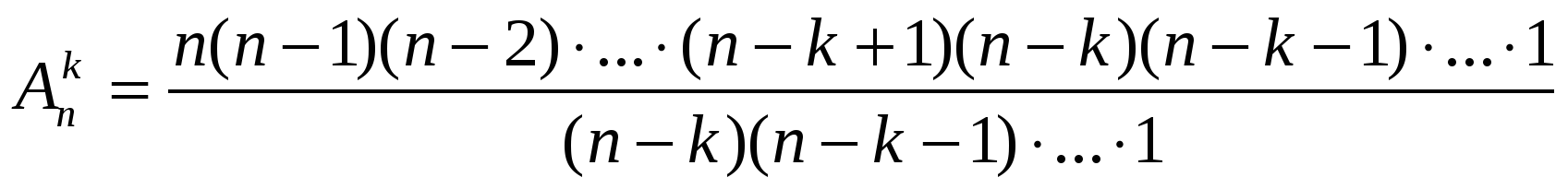 . (1)
. (1)
В числителе получилось произведение всех чисел от 1 до n. Такие произведения часто встречаются в комбинаторике. Их называют факториалами и обозначают n! (читают: «эн факториал»). Таким образом, формула (1) в этих обозначениях примет вид
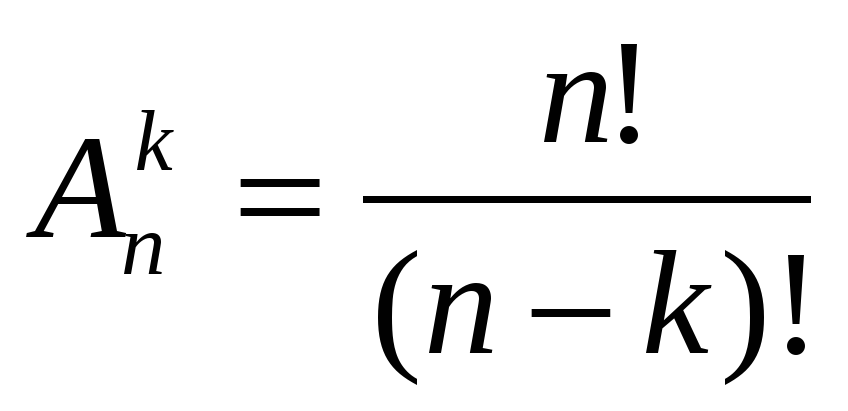 . (2)
. (2)
Полагают 1!=1. Это естественно. Но в дальнейшем нам встретится еще обозначение 0!. Принято считать, что 0!=1.
Задача 15. Научное общество состоит из 25 человек. Надо выбрать президента общества, вице-президента, ученого секретаря и казначея. Сколькими способами может быть сделан этот выбор, если каждый член общества может занимать лишь один пост?
Ответ: 25·24·23·22= =303600.
=303600.
Задача 16. В 8 «Г» классе 30 учащихся. Необходимо выбрать старшего дежурного и его заместителя. Сколько возможно различных комбинаций?
Ответ:  =30·29=870.
=30·29=870.
Задача 17. Сколько различных четырехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, если цифры в числе повторяться не могут?
Ответ:  =8·7·6·5=1680.
=8·7·6·5=1680.
Задача 18. Сколько словарей надо издать, чтобы можно было непосредственно выполнять переводы с любого из пяти языков: русского, английского, французского, немецкого, итальянского на любой другой из этих пяти языков? На сколько больше словарей придется издать, если число различных языков равно 10?
Ответ: 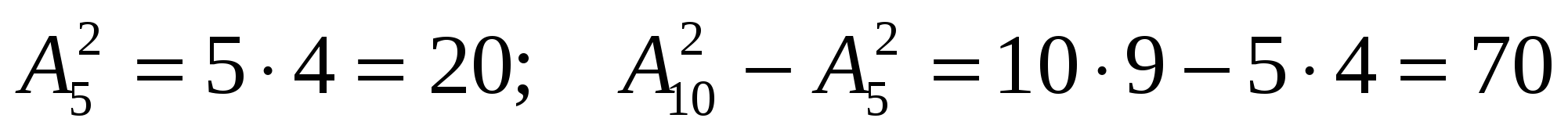 .
.
При составлении размещений без повторений из n элементов по k при kn мы получаем размещения, которые могли различаться и составом элементов, и порядком их расположения. Но если брать размещения, в которые входят все n элементов, то они могут отличаться друг от друга лишь порядком входящих в них элементов. Такие размещения из n элементов по n называют перестановками из n элементов.
Число перестановок из n элементов обозначают через Pn. Формула для Pn сразу получается из формулы для числа размещений без повторений.
Pn=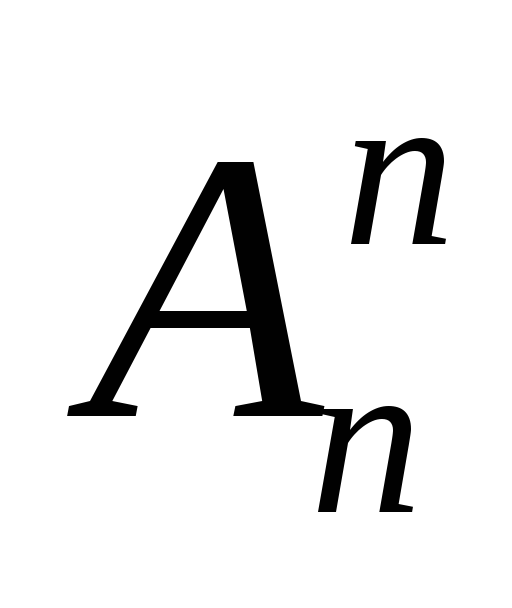 =n(n-1)(n-2)…1=n! (3)
=n(n-1)(n-2)…1=n! (3)
Задача 19. Сколько существует различных анаграмм слова СПОРТ?
Ответ: 5!=120.
Задача 20. Сколькими способами можно разослать 8 разных книг 8 различным адресатам?
Ответ: 8!=40320.
Задача 21. Студенту необходимо посетить 5 музеев с понедельника до пятницы - по одному музею в день. Сколько различных маршрутов он может составить?
Ответ: 5!=120.
Задача 22. На одной стене в музее в некотором зале должны висеть шесть картин. Сколько дней может быть разной выставка этих произведений, если от порядка картин меняется их целостное восприятие?
Ответ: 6!=720.
Задача 23. Сколько шестизначных кодов для открывания замка можно составить из цифр 2, 3, 5 и трех букв А, В и С, если в коде не должны повторяться ни буквы, ни цифры.
Ответ: 6!=720.
Задача 24. Сколько шестизначных кодов можно составить из цифр и букв предыдущей задачи, если
а) буква А должна быть первой?
б) цифра 1 не должна быть первой?
Ответ: а) 5!=120, б) 6!-5!=600.
«Спортлото»
Еще не так давно перед каждым тиражом «Спортлото» миллионы людей заполняли карточки, пытаясь угадать заветные 6 номеров из 49. У каждого была своя система – одни зачеркивали 6 номеров подряд, другие – через 3 на четвертый, третьи вспоминали дни, в которые одержала победу любимая команда и т.д. Сейчас существуют другие игры подобного рода.
В «Спортлото 6 из 49» из лототрона извлекаются 6 номеров из 49. Играющие тоже отмечают в карточке 6 номеров из 49, а выигрывают те карточки, в которых угаданы 3, 4, 5 или все 6 номеров. Сколькими же способами моно заполнить карточку «Спортлото», т.е. сколькими способами можно выбрать 6 номеров из 49?
Первое число можно выбрать 49 способами, второе – 48, третье - 47, четвертое - 46, пятое – 45, шестое – 44, но так как порядок чисел не важен, то произведение этих чисел нужно разделить на количество их перестановок, т.е. на 6!. Получиться число 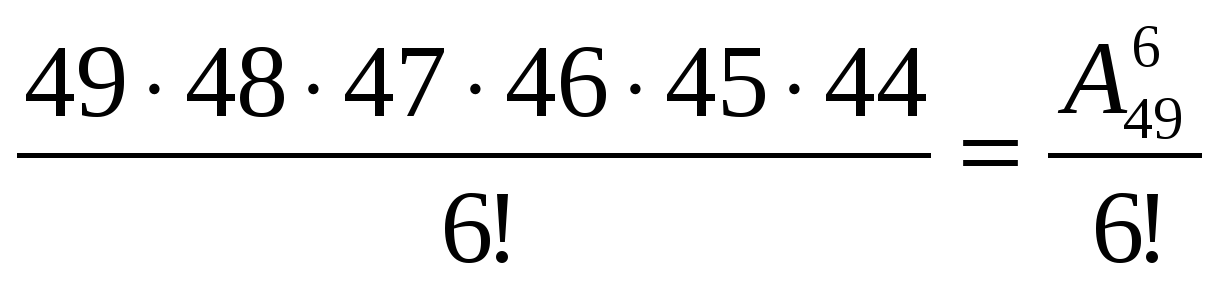 . Для решения аналогичных задач была введена формула сочетаний из n элементов по k:
. Для решения аналогичных задач была введена формула сочетаний из n элементов по k:
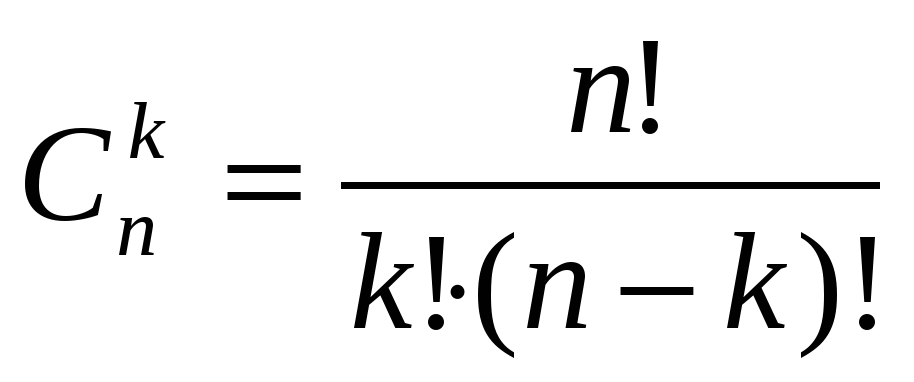 (4)
(4)
Итак, в тех случаях, когда нас не интересует порядок элементов, но интересует их состав, говорят о сочетаниях. Сочетаниями из n элементов по k называют любой выбор k элементов из имеющихся различных n элементов. По-французски С – первая буква слова combinations, откуда и произошло название раздела математики, занимающегося подсчетом различных комбинаций, соединений, сочетаний, перестановок каких-то элементов некоторых множеств – комбинаторики.
Задача 25. Сколькими способами можно выбрать три различные краски из имеющихся пяти различных красок?
Ответ: 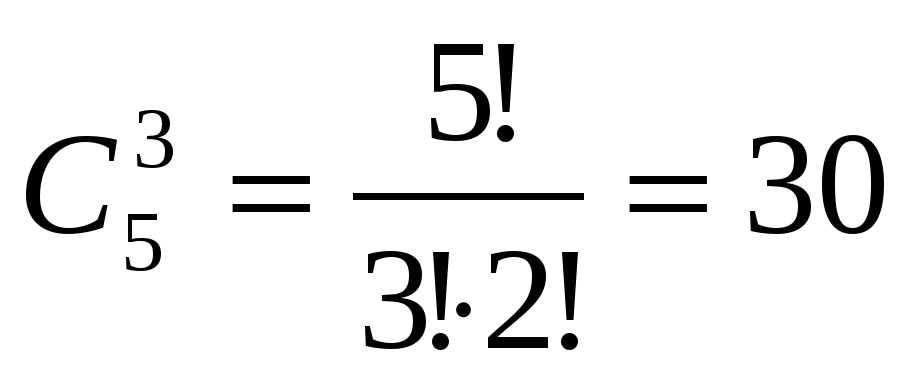 .
.
Задача 26. Из спортивного клуба, насчитывающего 30 членов, надо составить команду из четырех человек для участия в беге на 1000м. Сколькими способами это можно сделать?
Ответ:  .
.
Задача 27. Сколькими способами из колоды, содержащей 52 карты, можно вынуть 10 карт?
Ответ: 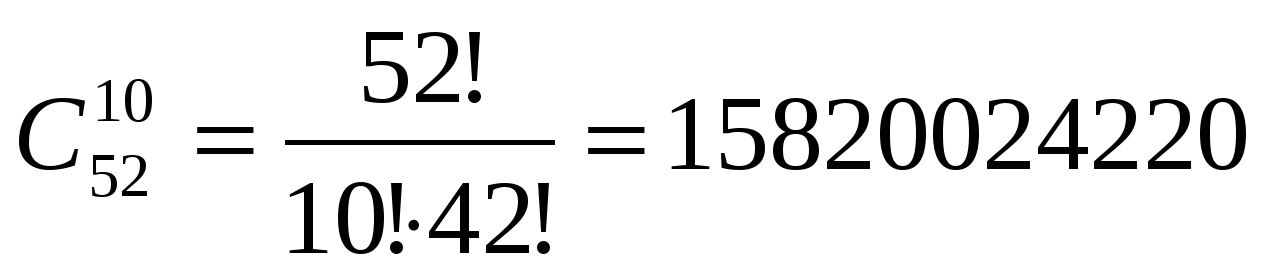 .
.
Задача 28. У Миши 6 друзей и ежедневно в течение 20 дней он приглашает к себе в гости троих из них так, что компания ни разу не повторяется. Действительно ли это у него получится?
Ответ: да получится, т.к. 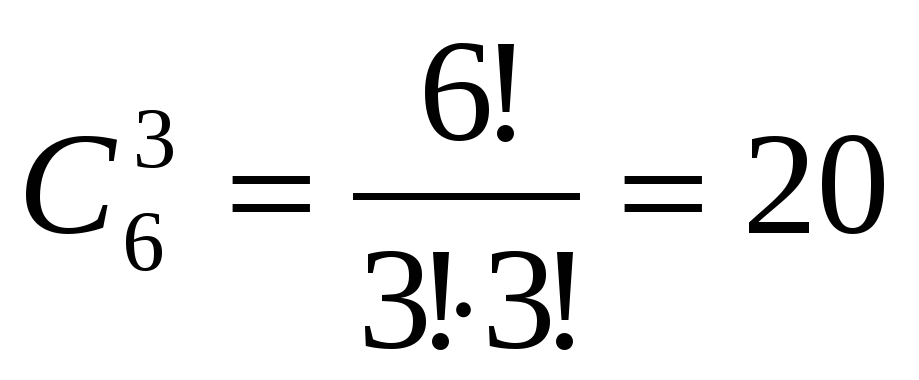 .
.
Задача 29. В спец.роте 75 солдат, пять офицеров и восемь сержантов. Необходимо выделить на охрану объектов восемь солдат, двоих сержантов и одного офицера. Сколько вариантов составить наряд существует?
Ответ: 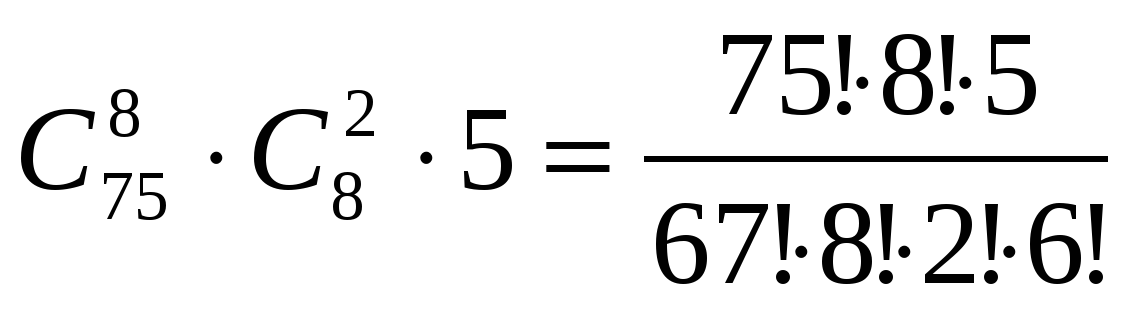 .
.
Задача 30. Из троих эпидемиологов и восьми терапевтов необходимо составить бригаду из шести врачей. Сколькими способами это можно сделать, если в нее обязательно должен войти хотя бы один эпидемиолог?
Ответ: 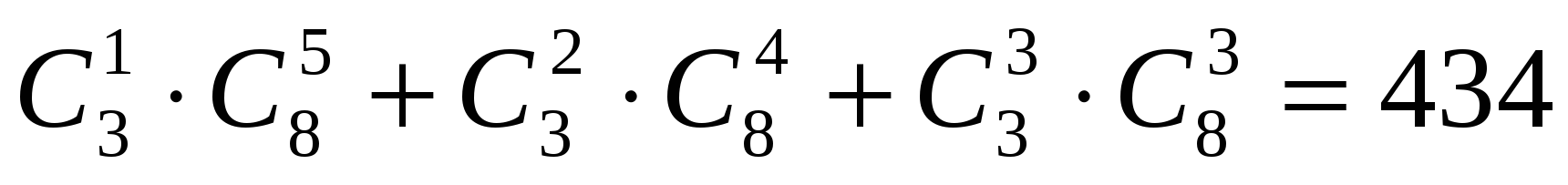 .
.
КОМБИНАТОРИКА В ВЕРОЯТНОСТНЫХ ЗАДАЧАХ
Пусть эксперимент может иметь всего n различных исходов. Те исходы испытания, которые приводят к появлению события А, называются исходами, благоприятствующими этому событию; пусть их число равно m. Если исходы опыта равновозможны, то при классическом определении вероятности вероятность события А равна отношению числа исходов опыта, благоприятствующих событию, к числу всех возможных исходов опыта, т.е.
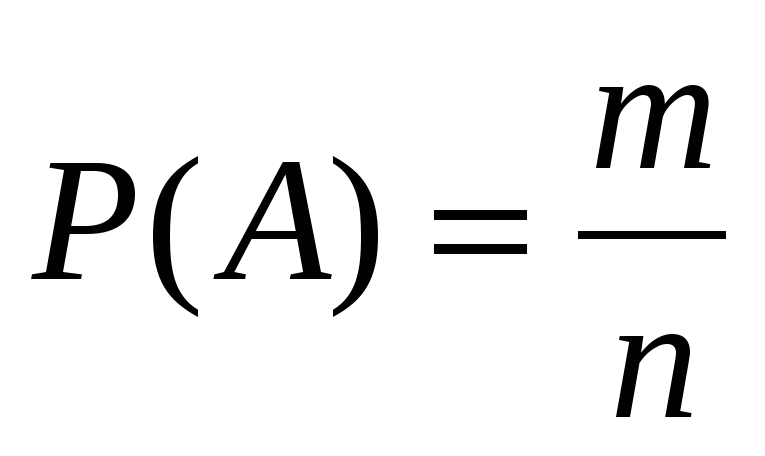 (5)
(5)
Задача 31. Найти вероятность выбора двух хороших деталей из 20, среди которых есть 5 бракованных.
Ответ: 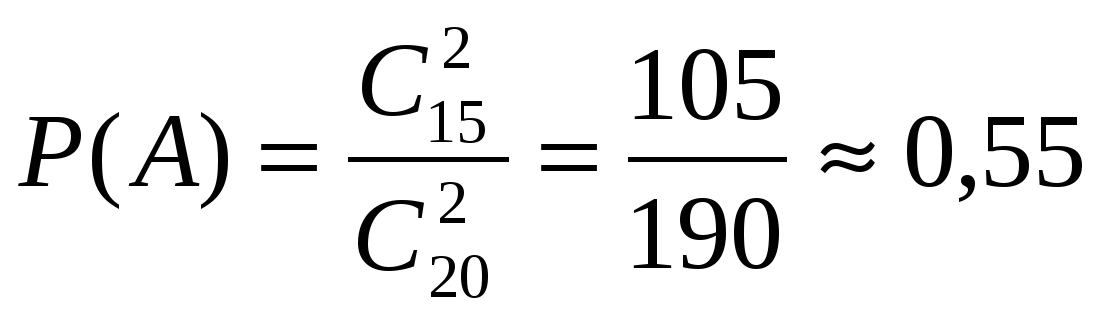 .
.
Задача 32. Каждый из пяти студентов может сдавать зачет в один из пяти назначенных дней. Выбор каждым студентом любого дня возможен. Какова вероятность того, что каждый день на зачет будет приходить только один из этих студентов?
Решение: Каждый из пяти студентов может выбрать любой из пяти дней, поэтому по дням явки на зачет студенты могут распределиться 55 способами. Благоприятствующие способы можно перебрать, если распределить студентов по одному на каждый день и рассмотреть всевозможные их перестановки. Таких перестановок существует 5!. Поэтому вероятность явки каждый день по студенту равна 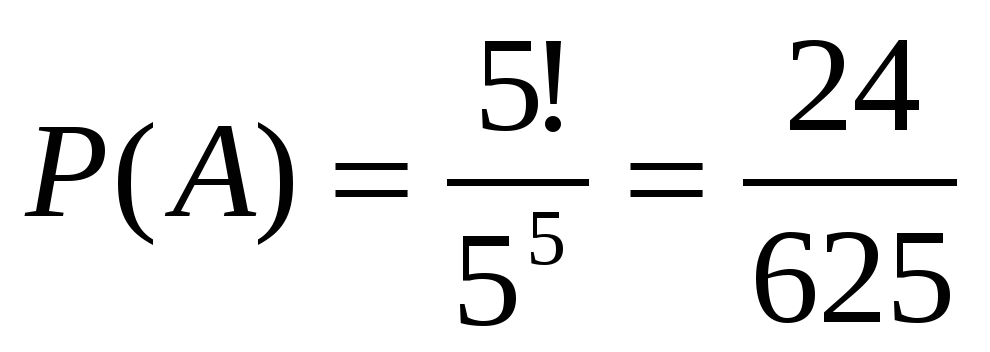 .
.
Задача 33. Из пяти букв разрезанной азбуки составлено слово «книга». Игривый котенок разбросал буквы. Какова вероятность, что пятилетний Андрей, не умеющий читать, вновь соберет слово «книга»?
Ответ: 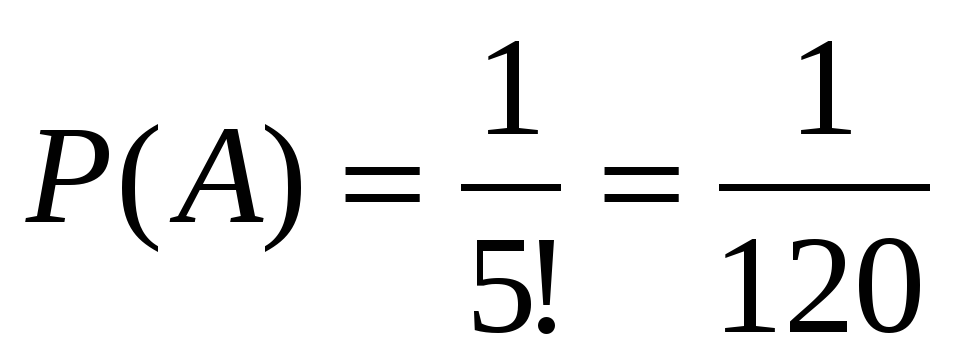 .
.
Задача 34. У Маши было четыре фантика от конфет «Мишка на севере», пять фантиков от конфет «Южные» и три фантика от конфет «Сливочные». К сожалению, один фантик она потеряла. Какова вероятность, что это фантик от «Мишки на севере»?
Ответ: 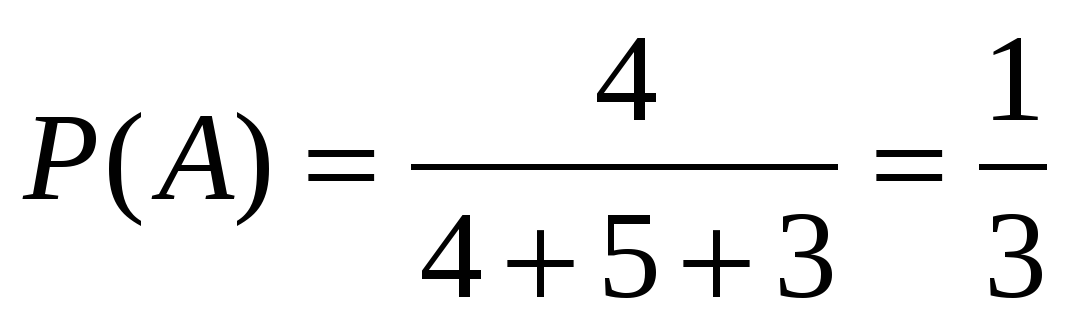 .
.
Задача 35. Найдите вероятность того, что случайно выбранная костяшка домино содержит менее семи точек (очков).
Решение. Всего 28 костяшек домино. Рассмотрим все костяшки, сумма очков на которых меньше семи: 0-0, 0-1,0-2,0-3,0-4,0-5,0-6, 1-1,1-2,1-3, 1-4, 1-5, 2-2, 2-3, 2-4, 3-3. Всего 16 костяшек. Вероятность равна .
Задача 36. На озере летала стая из 40 диких лебедей. Для изучения путей миграции 15 из них было окольцовано. Через месяц другая группа ученых захотела поставить свои метки (чипы) на лебедях. Какова вероятность того, что пойманные четыре диких лебедя окажутся окольцованными?
Решение. Выбрать 4 диких лебедя из сорока можно способами. Из 15 окольцованных лебедей четырех можно выбрать способами. Вероятность события (того, что четыре лебедя окажутся окольцованными) равна .
Задача 37. На школьном вечере каждому из двухсот учащихся дали занумерованную от 1 до 200 карточку. Какова вероятность того, что учащийся получит карточку с номером: а) кратным 7, б) кратным или 5, или 6?
Решение. а) Количество чисел, кратных 7 и меньших 200 равно . Следовательно, вероятность равна .
б) Количество чисел, кратных 5 и не меньших 200 равно 40.
Количество чисел, кратных 6 и меньших 200, равно .
Количество чисел, кратных 5 и 6, меньших 200, равно .
Следовательно, всего благоприятных исходов 40+33-6=71. Вероятность, того что на карточке будет номер, кратный или 5, или 6, равна =0,35.
Задача 38. Из колоды вынули 4 туза и 4 короля. Эти карты перемешали и разложили в ряд. Какова вероятность того, что все 4 короля окажутся расположенными рядом?
Решение. Обозначим событие: А - четыре короля оказались расположенными рядом. Общее число исходов равно количеству перестановок из 8 элементов 8!.
ΔΔΔΔ◊Θ◊Θ◊Θ◊Θ◊
Δ – короли, Θ – тузы, ◊ - возможные положения групп из четырех королей.
Найдем количество благоприятствующих исходов событию А. Если короли стоят рядом, то оставшиеся места тузы могут занимать 4! способами. Короли могут располагаться в пяти местах относительно тузов (см.рисунок), а также могут менять свой порядок. Поэтому всего 5! Способов расстановки королей. Тогда благоприятных исходов всего 5!·4!
Искомая вероятность события А равна .
СПИСОК ЛИТЕРАТУРЫ
Виленкин Н.Я., Виленкин А.Н., Виленкин П.А. Комбинаторика. – М.: ФИМА, МЦНМО, 2006.- 400с.
Спивак А.В. тысяча и одна задача по математике: КН. для учащихся 5-7 кл./А.В.Спивак. – 3-е изд. – М.: Просвещение, 2010. -207с.
Золотаревская Д.И. Теория вероятностей. Задачи с решениями: Учебное пособие. Изд. 6-е. – М.: Книжный дом «ЛИБРОКОМ», 2009. – 168с.
Практикум и индивидуальные задания по курсу теории вероятностей (типовые расчеты): Учебное пособие. – Спб.: Издательство «Лань», 2010. – 288с.
Шахмейстер А.Х. Комбинаторика. Статистика. Вероятность. – М.: Издательство МЦНМО: Спб.: «Петроглиф»: «Виктория плюс», 2010.- 296с.
Крупин В.Г., Туганбаев А.А. Теория вероятностей. - М.: Издательство «Факториал Пресс», 2006-128с.
20







 Если бы не было ограничения совместимости, то после каждого из 4 возможных способов выбора командира ai у нас было бы 3 варианта выбора инженера bj, а затем по 3 варианта выбора врача ck, и комбинаций было бы 4·3·3=36.
Если бы не было ограничения совместимости, то после каждого из 4 возможных способов выбора командира ai у нас было бы 3 варианта выбора инженера bj, а затем по 3 варианта выбора врача ck, и комбинаций было бы 4·3·3=36. 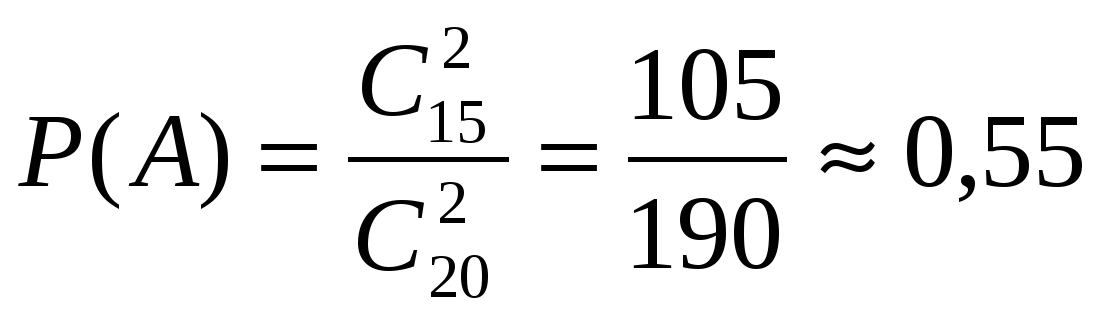 .
.


















