Формирование функциональной грамотности школьников на уроках математики
Федоткина Елена Павловна
учитель первой категории
МБОУ Надейковичская СШ имени И.П..Гоманкова»
Сегодня на первое место в мире выходит потребность быстро реагировать на все изменения, происходящие в жизни, умение самостоятельно находить, анализировать, применять информацию. Главным становится функциональная грамотность, так как это «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний». Одним из ее видов является математическая грамотность.
«Математическая грамотность – способность человека определять и понимать роль математики в мире, в котором он живет, высказывать хорошо обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину».
Выводы по результатам международных тестирований за последние несколько лет относительно математической грамотности российских школьников неутешительные: учащиеся показывают высокие результаты в применении известных алгоритмов и процедур, но результаты выполнения заданий, связанных с анализом информации, явно ниже.
Это задания:
на применение знаний в практических, жизненных ситуациях;
в которых содержание представлено в необычной, нестандартной форме;
требующие проведения анализа имеющихся данных или их интерпретации и др.
Термин «грамотность» в данном исследовании имеет специфическое содержание. Под грамотностью здесь понимается не мастерское владение математическими знаниями в рамках школьной программы, а способность функционально использовать эти знания.
Под математической грамотностью понимается способность учащихся:
распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики;
формировать эти проблемы на языке математики;
решать эти проблемы, используя математические факты и методы;
анализировать и использовать математические методы решения;
интерпретировать полученные результаты с учетом поставленной проблемы;
формулировать и записывать результаты решения.
Компоненты математической грамотности:
- воспроизведение математических фактов, методов и выполнение вычислений
- установление связей и интеграции материала из разных математических тем, необходимых для решения поставленной задачи
- математические размышления, требующие обобщения и интуиции
В 2021 году основное направление исследования PISA - математическая грамотность.
Исследование PISA-2021 будет измерять, насколько эффективно образовательные системы стран готовят учащихся к использованию математики во всех аспектах их личной, общественной и профессиональной жизни.
В определении математической грамотности особое внимание уделяется использованию математики для решения практических задач в различных контекстах.
Задания PISA проверяют не заученный материал по математике, а владение учеником компетенциями в различных контекстах этих предметов и межпредметного взаимодействия: здоровье человека, природные ресурсы, окружающая среда, экология, открытия в области науки и технологии. Существуют интерактивные задания, направленные на наблюдение за каким-то объектом, в которых нужно сделать вывод о том, как функционирует этот объект. Есть задания с аналитическим решением, в которых стоит задача предусмотреть дальнейшее развитие событий или действие каких-то предметов.
«Математическая грамотность включает в себя математические компетентности, которые можно формировать через специально разработанную систему задач:
1 группа – задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления;
2 группа – задачи, в которых требуется установить связи и интегрировать материал из разных областей математики;
3 группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую средствами математики, построить модель решения.
Первый уровень – воспроизведение. Включает проверку определений или простых вычислений, характерных для обычной проверки математической подготовки учащихся. Для проверки достижения первого уровня компетентности в основном предлагаются традиционные учебные задачи, требующие знание математических фактов, воспроизведение определений математических объектов и их свойств, применение стандартных алгоритмов и методов решения, работа с формулами, выполнение вычислений. Так как способы решения в основном стандартные, то запись самого решения не представляет интереса, и поэтому используются задания двух типов – с выбором ответа и с кратким свободным ответом, когда ответ дается в виде числа, выражения, слова, а решение не приводится.
Второй уровень – установление связей. Второму уровню компетентности присущи умения устанавливать связи между различными темами программы по математике и интегрировать информацию, необходимую для решения задачи. От учащихся требуется самостоятельно выбрать соответствующий метод решения и необходимые математические инструменты. Ситуации, рассматриваемые в задачах, должны быть нестандартными, но не требовать высокого уровня математизации.
Третий уровень– размышления. Включает проверку математического мышления, умения обобщать, глубоко понимать, использовать интуицию
Для этого разрабатываются более сложные задачи, в которых, прежде всего, необходимо «математизировать» предложенную ситуацию. Эта процедура состоит из двух этапов: выделение проблемы, которая решается средствами математики, и ее формулировка; разработка соответствующей математической модели, решение и его интерпретация согласно предложенной в задании ситуации.
Развивать математическую грамотность надо постепенно. Регулярно включать в ход урока задания на «изменение и зависимости», «пространство и форма», «неопределенность», «количественные рассуждения» и т.п..
Эти задания можно использовать по усмотрению учителя:
Как игровой момент на уроке;
Как проблемный элемент в начале урока;
Как задание – «толчок» к созданию гипотезы для исследовательского проекта;
Как задание для смены деятельности на уроке;
Как модель реальной жизненной ситуации, иллюстрирующей необходимость изучения какого- либо понятия на уроке;
Как задание, устанавливающее межпредметные связи в процессе обучения;
Некоторые задания заставят сформулировать свою точку зрения и найти аргументы для её защиты;
Можно собрать задания одного типа и провести урок, в соответветствии с какой- то образовательной технологией;
Можно все задачи объединить в группы и создать свой элективный курс по развитию математического мышления;
Задания такого типа можно включать в школьные олимпиады, математические викторины;
Задачи на развитие математического мышления могут стать основой для внеклассного мероприятия в рамках декады математики.
На уроках я учу детей ставить цели и планировать деятельность по их достижению, учу добывать нужную информацию, используя доступные источники (справочники, учебники, словари, СМИ), передавать её. Не забываю и о том, что детям необходимо уметь высказывать и аргументированно отстаивать своё мнение. В ходе урока уметь грамотно пользоваться математическими терминами. Прививать навыки самоконтроля и взаимоконтроля. Следовательно, функциональная математическая грамотность включает в себя навыки поиска и интерпретации математической информации, решения математических задач в различных жизненных ситуациях. Информацию я представляю в виде рисунков, цифр, математических символов, формул, диаграмм, карт, таблиц, текста, а также показываю с помощью технических способов визуализации материала.
Такое поведение включает в себя навыки решения проблем в реальной жизни посредством использования математической информации, включающей в себя: количества и числа, размерные величины, схемы и диаграммы, связи данных, вероятность и др.
Примеры задач первого уровня:
5 класс
1. В магазине детских игрушек продают двухколесные и трехколесные велосипеды, причем тех и других поровну. Сколько колес может быть у всех велосипедов вместе? А) 16; В) 24; С) 25; D) 28; Е) 33.
Решение. Так как количество двух- и трехколесных велосипедов одинаково, то число колес у всех велосипедов должно быть кратно 5.
Правильный ответ С.
2. Витя вылепил игрушку из глины за 40 мин. На раскрашивание этой игрушки он потратил времени в 2 раза меньше, а потом в течение 1 ч игрушка обжигалась в печи. Сколько времени ушло на изготовление игрушки?
3.В парнике выращивали помидоры, причём часть из них отправляли на продажу, а остальное оставляли на семена. Сколько килограммов помидоров оставили на семена, если в магазин каждую неделю отправляли по72 кг помидоров, а всего за месяц собрали 300кг помидоров?
4. Сколько процентов сэкономит покупатель, если во время распродажи зимнюю куртку можно купить за 3 тыс. рублей, а в сезон эта же куртка стоила 7,5 тыс. рублей?
А) 60%; В) 150%; С) 90%; D) 87,5%; Е) 78,5%
Решение. Так как стоимость куртки после скидки стала на 4,5 тыс рублей меньше, то следует узнать, сколько процентов составит эта разница от первоначальной цены, то есть от 7,5 тыс рублей.
Правильный ответ А.
5. Трое друзей собрались в поход. Сложились и купили палатку. Первый заплатил 60% от общей суммы, второй 40% оставшейся суммы, а третий последние 30 долларов. Сколько стоит палатка? Сколько заплатил каждый из друзей?
А) 120долл.; В) 150долл.; С) 90долл; D) 125долл; Е) 100 долл.
Решение. Предположим х долларов – стоимость палатки, тогда первый заплатил 0,6х, а второй – 0,4(х-0,6х)=0,16х, значит, третьему осталось заплатить х-(0,6х+0,16х)=0,24х. Зная, что третий заплатил 30 долларов, составим уравнение: 0,24х=30, откуда х = 125. Стоимость палатки 125 долларов. Правильный ответ D.
Задачи второго уровня:
5 класс
1. Три друга играют в игру: ведущий раздает 8 карточек, пронумерованных от 1 до 8 двум играющим. Первому – 3 карточки, второму -5 карточек. Оказалось, что сумма номеров карточек у них одинакова. Третий участник игры утверждает:
1)три карточки с нечетными номерами у второго игрока;
2) карточка с номером 2 у второго игрока;
3)карточка с номером 1 не у первого игрока.
Прав ли он?
Решение. Поскольку суммы номеров у игроков одинаковые, то они составят половину суммы всех чисел от 1 до 8, то есть 18. У игрока с тремя карточками это могут быть карточки с номерами 5, 6 и 7; 4, 6 и 8 или 3, 7 и 8. В остальных случаях суммы получаются менее 18. Значит, у второго игрока могут быть карточки с номерами 1, 2, 3, 4 и 8; 1, 2, 3, 5 и 7 или 1, 2, 4, 5 и 6 соответственно. Таким образом, первое высказывание неверно, второе верно, третье верно. Ответ: 1)нет, 2) да, 3) да.
2. Математик, свидетель дорожно-транспортного происшествия, запомнил, что номер машины виновника ДТП – четырехзначное число, которое делится на 19 и оканчивается на 19. Сколько машин должны проверить работники автоинспекции, чтобы установить виновника ДТП?
3. Печенье упаковали в пачки по 250 г. Пачки сложили в ящик в 4 слоя. Каждый слой имеет 5 рядов по 6 пачек в каждом. Выдержит ли ящик, если максимальная масса, на которую он рассчитан, равна 32 кг?
Определи стоимость приготовления 1 кг салата «Греческий», если для этого требуется:
Помидоры – 4 штуки
Огурец-3 штуки
Перец – 2 штуки
Маслины-1 банка
Сыр -1 упаковка
Листья салата-1 упаковка
Помидоры стоят 11 рублей за штуку, банка маслин стоит 52 рубля, огурцы – 8 рублей за штуку, упаковка сыра стоит 89 рублей, перец-24 рубля за штуку, упаковка листьев салата стоит 35 рублей.
4.Врачи рекомендуют в первый день отдыха на море незагоревшему человеку проводить на солнце 20 мин, а потом каждый день можно увеличивать время пребывания на солнце на 5 мин. Лена начала загорать в понедельник. Сколько времени она может находиться на солнце в ближайшее воскресенье?
Задача третьего уровня:
1.Банк Х меняет рубли на тугрики по 3000 рублей за тугрик, и еще берет 7000 рублей за право обмена независимо от меняемой суммы. Банк У берет за тугрик 3020 рублей, а за право обмена берет 1 тугрик (тоже независимо от меняемой суммы). Турист установил, что ему все равно, в каком из банков менять деньги. Какую сумму он собирается менять?
Решение. Предположим, турист собирается получить х тугриков. В банке Х он заплатит за них (3000х + 7000) рублей, а в банке У – 3020(х + 1) рублей.
Составим и решим уравнение 3000х + 7000 = 3020(х + 1), откуда получаем х = 199. Таким образом, турист располагает суммой, равной 3020×200 = 60400. Ответ: турист собирается менять 60400 рублей, за которые он получит 199 тугриков.
2. 8 класс, тема «Числовые промежутки»
Задание направлено на анализ полученного результата каждой строки, нахождение закономерностей и возможность проверки своей гипотезы в виде заполнения пропуска.
Задание. Заполнить пропуски таблицы:
|
1
| Трель | мель | ель |
| 5 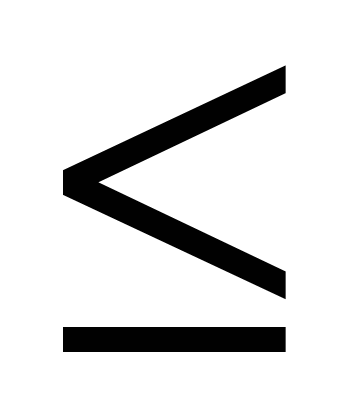 х х 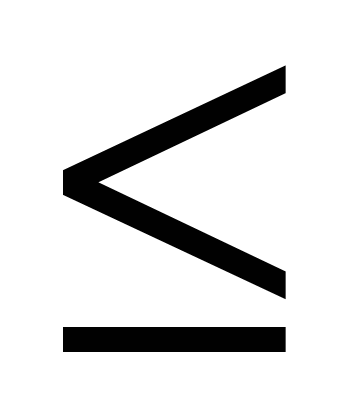 10 10 | ( –7 ; 9) | ? |
|
2
| х 3 | (-1 ; 7) | [-1 ; 3 ) |
| настил | крокодил | ? |
|
3
| ровесник | 3 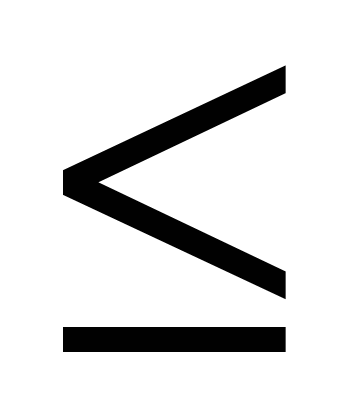 х х | вес |
| Транспортир | 5 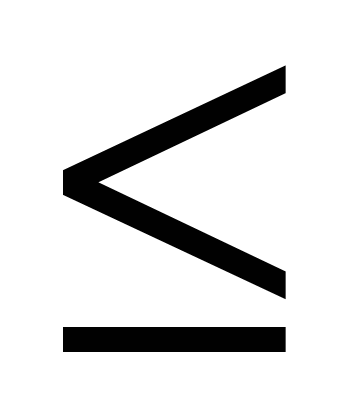 х х 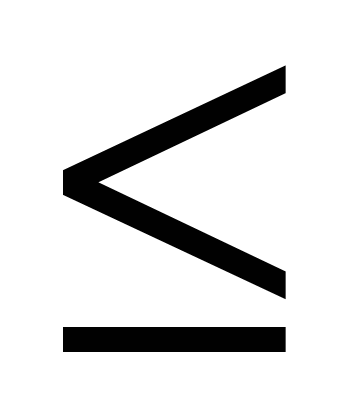 9 9 | ? |
|
4
| трапеция | трап | х |
| Свисток | ток | ? |
|
5
| Транспорт |
|
| 1 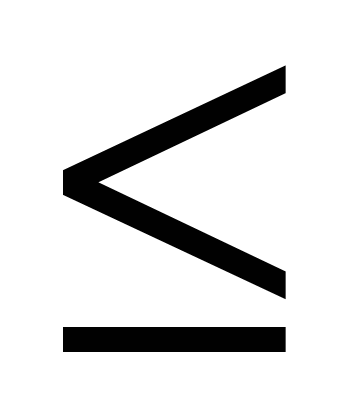 х 5 х 5 | 1 х 5 |
|
| трап | ? |
|
|
6
| рак | низ | карниз |
| -4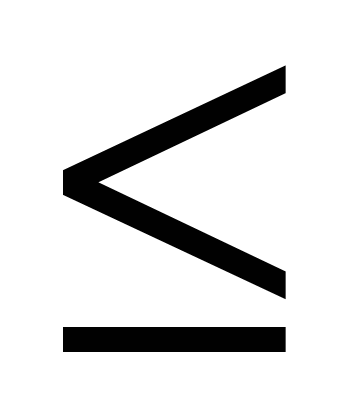 2 2 | -1  5 5 | ? |
|
7
| - 2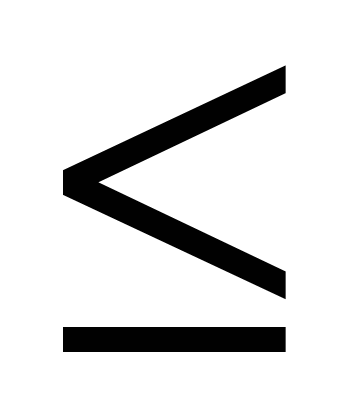 5 5 | х 3 | 3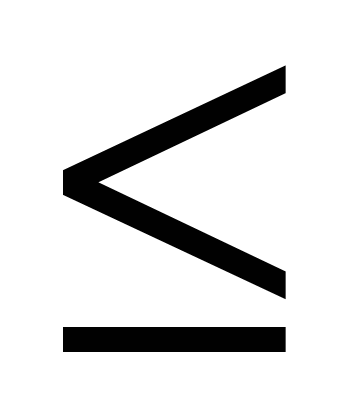 5 5 |
| лось | кость | ? |
|
8
| Дом | ель | модель |
| х | х 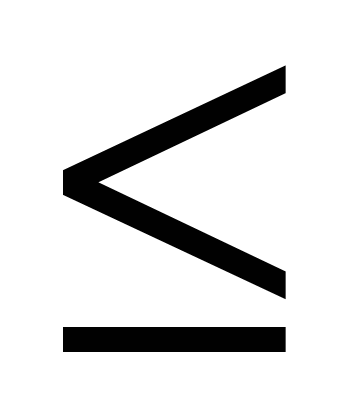 0 0 | ? |
Практико-ориентированные задания
1.Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 8 дней. В одной упаковке 10 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
2.Пакетик сока стоит 80 тенге. Какое наибольшее число пакетиков сока можно купить на 500 тенге? (Хватит ли денег Вите, если он захочет купить сок себе и угостить пятерых друзей; если «да», то сколько денег у него останется?)
3.Аня купила месячный проездной билет на автобус. За месяц она сделала 112 поездок. Сколько тенге она сэкономила, если проездной билет стоит 7000 тенге, а разовая поездка 75 тенге?
4. В супермаркете проходит рекламная акция: заплатив за две шоколадки, покупатель получает три шоколадки (одна шоколадка в подарок). Шоколадка стоит 220 тг. Какое наибольшее число шоколадок можно получить на1200 тг?
5.В упаковочную коробку должен поместиться набор деталей конструктора объёмом 0,064 м3. Какими должны быть размеры коробки в форме куба, если между деталями конструктора и коробкой по длине, ширине и высоте должно оставаться свободное пространство в 2 см? Вычислите площадь поверхности коробки и её объём. Ответы округлите до тысячных
Все эти задания направлены на развитие математической и естественнонаучной грамотности, которое предполагает способность учащихся использовать знания, приобретенные ими за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.
Сегодня учитель перестал быть для ученика «единственным источником информации». Вовлечь каждого ученика в процесс обучения, суметь выслушать его, сделать его своим помощником или ассистентом, посмотреть глазами самого ребёнка на беспокоящую его проблему – вот задача для современного учителя.
В результате такой работы, учащиеся не только знакомятся с заданиями нестандартного характера, но и повышают математическую функциональную грамотность: расширяют свои знания, развивают образное мышление, находят взаимосвязь между различными явлениями, учатся объяснять причины наблюдаемых природных явлений, познают проявления физических закономерностей во многих областях и сферах человеческой деятельности: производственной, научно-исследовательской, социально-бытовой. Также учатся применять собственные знания для решения проблем, максимально приближенных к тем, с которыми приходится сталкиваться в реальной жизни.
«Красоту математики можно увидеть глазами, можно почувствовать сердцем, но объять ее можно только умом»
Шалва Александрович Амонашвили
8

















