Формирование функциональной грамотности на уроках математики.
Функциональная математическая грамотность – это способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе.
Как учитель, я прекрасно понимаю важность развития функциональной грамотности моих учеников. Одним из способов развития математической грамотности является повышение мышления у учащихся через элементы развивающего обучения, например, при работе, над текстовой задачей. Решение текстовых задач - основа, в которой проявляются все знания, умения, возможность анализировать, синтезировать и оценивать как собственные силы, так и учебный материал. А это и есть продуктивный уровень, характеризующий как общую, так и функциональную грамотность учащихся.
Наибольший эффект при этом у меня достигается в результате применения различных форм работы над задачей:
1. Работа над решенной задачей.
2. Решение задач различными способами.
3. Моделирование задачи
4. Работа над структурой задачи.
5. Объяснение готового решения.
6. Закончи решение задачи.
7. Изменение вопроса задачи.
8. Решение задачи с лишними или недостающими данными.
9. Составление различных выражений к «данным» задачи.
10. Выбор выражений, являющихся решением задачи.
11. Выбор способа записи решения (уравнение, выражение, по действиям).
12. Сравнение задач и их решений.
13. Выбор решения из двух предложенных.
14. Изменение условия, чтобы задача решалась другим действием.
15. Составление задач по схемам, рисункам, словам.
16. Составление аналогичной задачи.
17. Составление и решение обратных задач.
В нашем УМК все формы работы над текстовой задачей представлены авторами.
Но функциональная математическая грамотность включает в себя математические компетентности, которые можно формировать через специально разработанную систему задач:
1 группа - задачи, в которых требуется воспроизвести факты и методы, выполнить вычисления;
2 группа – задачи, в которых требуется установить связи и интегрировать материал из разных областей математики;
3 группа – задачи, в которых требуется выделить в жизненных ситуациях проблему, решаемую средствами математики, построить модель решения.
Виды задач:
1. Компетентностные задачи
2. Нестандартные задачи
3. Комбинаторные задачи
4. Задачи повышенной трудности (логические задачи)
Рассмотрим компетентностные задачи.
Компетентностно-ориентированные задания – это деятельностное задание, оно моделирует практическую, жизненную ситуацию, строится на актуальном для учащихся материале.
Компетентностно-ориентированные задания изменяют организацию традиционного урока. Они базируются на знаниях и умениях, но требуют умения применять накопленные знания в практической деятельности. Цель этих заданий – «окунуть» учащихся в решение «жизненной» задачи.
После решения задаю ученикам вопрос: «Где в жизни вам пригодятся эти знания и умения?»
Например:
В выставочном зале прямоугольной формы надо настелить линолеум. Длина зала 24 м и ширина 16 м. В каждом рулоне 12 м линолеума шириной 1600 см. Сколько потребуется рулонов?
Решение:
24·16=384 кв м- площадь
1600см=16 м, 1м =100см
1600:100=16 м
12·16=192 кв м - площадь 1 линолеумного рулона
384:192= 2 рулона нужно.
Нестандартные задачи – это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Такие задачи обычно включены в олимпиады.
Правил решения задач нестандартного характера нет. Но великими решателями задач найдено ряд общих рекомендаций-указаний, которыми можно пользоваться при решении. Эти советы-рекомендации назовем эвристическими правилами.
Чтобы решить нестандартную задачу, надо составить план (найти ход) решения - не обязательно точный и полный перечень действий. Большей частью это даже не ход, а только идея, а всё остальное возникает в процессе решения. Иногда оказывается, что идея не верна, и надо всё начинать снова. Процесс этот не поддается точному определению, но говорить при этом о каких-то общепринятых шагах можно, хотя поиску решения задач нельзя научить, можно лишь самому научиться.
Например: Придя из магазина мама положила конфеты на 6 тарелок. На первую - 1 конфету, на каждую следующую - на 2 конфеты больше, чем на предыдущую. Как можно разделить их на троих поровну не снимая с тарелки? Одна из дочерей догадалась. А ты догадаешься?
Решение:
1 тарелка - 1 конфета
2 тарелка - 1+2=3 конфеты
3 тарелка - 3+2=5 конфет
4 тарелка - 5+2=7 конфет
5 тарелка - 7+2=9 конфет
6 тарелка - 9+2=11 конфет
Значит, всего конфет было: 1+3+5+7+9+11=1+5+(3+7)+(9+11)=6+10+20=36
Следовательно, каждому получается по 36:3=12 конфет, это можно получить, не снимая с тарелки, таким образом:
Первому - 1 и 6 тарелка - 1+11=12 конфет
Второму - 2 и 5 тарелка - 3+9=12 конфет
Третьему - 3 и 4 тарелка - 5+7=12 конфет
Комбинаторные задачи
Комбинаторика - это раздел математики, в котором исследуются и решаются задачи выбора элементов из исходного множества и расположения их в некоторой комбинации, составляемой по заданным правилам.
Учитывая возрастные особенности младших школьников, комбинаторные задачи решаются методом на основе рассуждений учащихся, составлением графов, размещением, таблиц, «древо» решений.
Например, комбинаторная задача размещение 1) когда цифры в записи числа повторяются; 2) когда цифры в записи числа не повторяются
Из цифр 1, 2, 3, 4, 5, 6 составь все возможные трехзначные числа.
Решение:
Считаем сначала сколько можно составить трёхзначных чисел для одной цифры из шести. Путём несложного математического подсчёта получаем двадцать чисел для одной цифры. Дальше умножаем шесть на двадцать, получаем 120 (сто двадцать). Итак, получилось, что из цифр 1,2,3,4,5,6, можно составить сто двадцать чисел.
123, 124, 125, 126, 132, 134, 135, 136, 142, 143, 145, 146, 152, 153, 154, 156, 162, 163, 164, 165.
20 чисел для одной цифры, цифр 6. Умножаем 20 на 6 получаем 120. Итак, из имеющихся цифр можно составить 120 трёхзначных чисел, где одна буква не ставится дважды в одно число.
При такой постановке вопроса мы должны рассмотреть случаи:
1) когда цифры в записи числа повторяются
2) когда цифры в записи числа не повторяются.
Рассмотрим первый случай, когда цифры повторяются.
Отметим место каждой цифры звездочкой. Сколько цифр претендует на первое место? На второе место? На третье?
6 х 6 х 6 =216
Рассмотрим второй случай, когда цифры не повторяются.
Отметим место каждой цифры звездочкой. Сколько цифр претендует на первое место? На второе место? На третье?
6 х 5 х 4 =120
Например, комбинаторная задача составление таблицы.
Для начинки пирога бабушка решила смешать два продукта. Сколько различных пирогов может испечь бабушка, если для начинки у нее есть картофель (К), грибы (Г), яблоки (Я), мясо (М)?
Составление таблицы:
|
| К | Г | Я | М |
|
|
| К |
|
|
|
|
|
|
| Г | ГК |
|
|
|
|
|
| Я | ЯК | ЯГ |
|
|
|
|
| М | МК | МГ | МЯ |
|
Ответ: 6 различных пирогов может испечь бабушка.
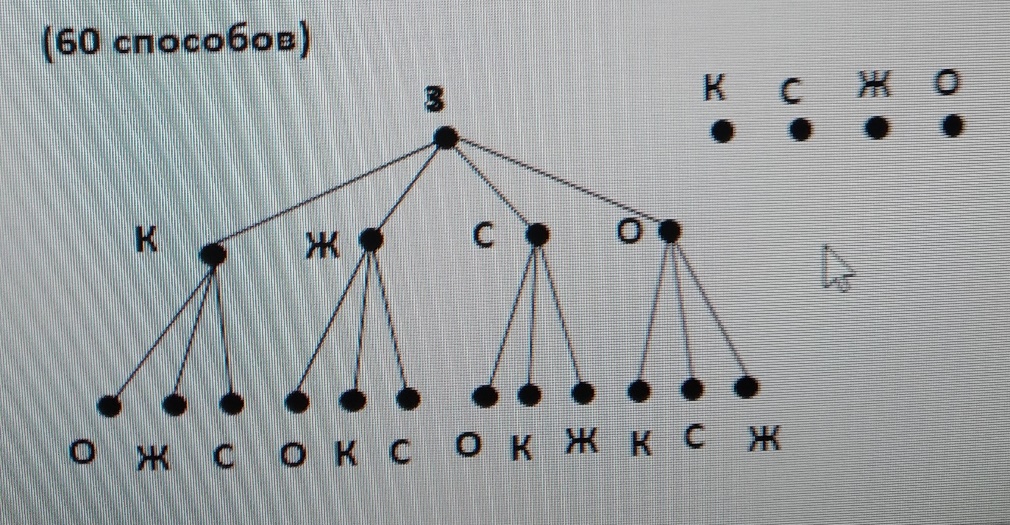
Например: комбинаторная задача «древо» решений.
Есть краски зелёного, красного, жёлтого, синего, оранжевого цветов. Сколькими способами можно раскрасить трёхэтажные домики в 3 цвета, при условии, что цвета не должны повторяться? (12 · 5 = 60)
Задачи повышенной трудности (логические задачи)
Для развития логического мышления в обучение я включаю развивающие задания (внимание, воображение, память, мышление) и нестандартные задачи.
Развивающие задания у нас включены в учебнике на полях, а также под номерами заданий. Обычно требуют ответов на вопросы.
«Что общего?», «Что объединяет?», «Что лишнее?» - эти задания учат выделять существенные признаки, учат ребёнка сравнивать, учат классифицировать. Например: «Сравни», «Найди лишнюю бусину».
Задания, совершенствующие воображения: сравни все фигуры между собой: чем они похожи, чем различаются. Дорисуй в каждой фигуре по одному квадрату так, чтобы все фигуры отличались друг от друга только цветом.
Задания, развивающие память: определи для каждой таблицы, какую картинку надо вставить в пустую клетку.
Задания, требующие концентрации всех познавательных процессов: внимания, памяти, воображения: шёл мужик в Москву, а навстречу ему шли 7 богомолок, у каждой из них было по мешку, а в каждом мешке по коту. Сколько существ направлялось в Москву?
Технологию работы над нестандартной задачей продумываю так, чтобы был каждый вопрос построен правильно. Тогда учащиеся научатся не просто угадывать ответ, а будут применять конкретные способы и методы к каждой конкретной задаче.
При решении нестандартные задач использую следующие методы: метод рассуждений, метод таблиц, метод графов, метод блок – схем, метод кругов Эйлера, метод бильярда.
Метод рассуждений – это самый примитивный способ. Этим способом решаются самые простые логические задачи. Он состоит в том, что провожу рассуждения, используя последовательно все условия задачи, и прихожу к выводу, который и будет являться ответом задачи.
Например: у трёх девочек – Лизы, Маши, Вики – шапочки разного цветы: красного, белого и синего. У кого какого цвета шапочка, если все записи неверные? У Лизы белая шапочка, у Маши белая или синяя шапочка, у Вики красная шапочка.
(Начни рассуждать так: запись у Маши белая или синяя шапочка неверна. Значит у Маши… Ответ: У Маши – красная, у Лизы – синяя, у Вики – белая)
Метод таблиц – этот приём заключается в построении таблиц. Таблицы не только позволяют наглядно представить условие задачи, но позволяют делать правильные логические выводы в ходе решения задачи.
Например: у трёх девочек – Лизы, Маши, Вики – шапочки разного цветы: красного, белого и синего. У кого какого цвета шапочка, если все записи неверные? У Лизы белая шапочка, у Маши белая или синяя шапочка, у Вики красная шапочка.
Эту задачу эффективнее решить способом составления таблиц.
|
| Лиза | Маша | Вика |
|
|
| Красная шапочка | _ | + | _ |
| Белая шапочка | _ | - | + |
| Синяя шапочка | + | - | _ |
Метод графов - объекты изображаются точками, а отношения между ними – линиями. При решении комбинаторных задач (задач на взвешивания, переливания, подсчет вариантов и т. д.) с помощью графов описывается переход из одного состояния объектов в другое.
Например: Люба пришла из школы раньше, чем Надя, а Надя – раньше, чем Саша. Кто из них домой пришёл последний? (Ответ: Последней пришла Саша, второй пришла Надя, первой пришла –Люба)

Метод блок – схем - простейший прием решения таких задач состоит в переборе возможных вариантов. Оформить её можно в виде схемы. Составленная блок-схема является программой, выполнение которой может привести нас к решению задачи.
Например: вспомни состав числа 10 и ответь на вопросы задачи. За карандаш и ластик заплатили 10 руб. Карандаш на 4 рубля дороже ластика. Сколько стоит ластик? Сколько стоит карандаш?
Решение: 1) 10 – 4 = 6; 2) 6:2 =3; 3) 3 + 4 = 7; 4) 3 + 7 = 10.

Метод кругов Эйлера - нужно нарисовать на бумаге один, два или три пересекающихся круга разного цвета.
Например: 20 человек в классе занимались бегом, а 17 – плаванием. 11 человек занимались и бегом, и плаванием. Сколько человек в классе?

Метод Бильярда - представьте себе горизонтальный бильярдный стол произвольной формы, но без луз. По этому столу без трения движется точечный шар, абсолютно упруго отражаясь от бортов стола. Спрашивается, какой может быть траектория этого шарика? Поиски ответа на этот вопрос и послужили появлению теории математического бильярда или теории траекторий. Метод бильярда применяю для решения задач на переливание. Но такие задачи решают в 3-4 классах, а не в первом.
Например. Имеются три сосуда вместимостью 8, 5 и 3 литра. Наибольший сосуд полон молока. Как разделить это молоко на две равные части, используя остальные сосуды?
Решение.
В таблице указан объем молока в литрах после каждого переливания.
8-литровый сосуд 5-литровый сосуд 3-литровый сосуд
8 0 0
3 5 0
3 2 3
6 2 0
6 0 2
1 5 2
1 4 3
4 4 0
После переливания оказалось по 4 л молока в 8-литровом и 5-литровом сосудах, а это и требовалось.
Вывод: Систематическое использование на уроках математики специальных задач и заданий, формирует и развивает функциональную математическую грамотность младших школьников, позволяет более уверенно ориентироваться в простейших закономерностях окружающей их действительности и активнее использовать математические знания в повседневной жизни.
7