Формирование приемов смыслового чтения на уроках математики в начальной школе.

Формирование приемов смыслового чтения на уроках математики в начальной школе.

Активность личности в обучении является важнейшим фактором для достижения целей обучения, общего развития личности.

Новый стандарт предъявляет новые требования к результатам начального образования

Выпускник начальной школы должен не только владеть системой знаний, умений и навыков. В проекте стандарта сказано, что ребёнок, оканчивающий начальную школу, – это человек любознательный, интересующийся, активно познающий мир; умеющий учиться, способный к организации собственной деятельности.

Интерес к чтению возникает в том случае, когда читатель свободно владеет осознанным чтением и у него развиты учебно-познавательные мотивы чтения. Одним из вариантов повышения качества чтения в начальной школе является целенаправленное управление обучением чтению. Чтобы чтение было эффективным, важно научить ребенка пользоваться книгой.

Приведу примеры которые я использую на уроках курса «Математика»

Использование приемов смыслового чтения

на уроках математики в начальной школе

Опыт работы показывает, что современный ученик не умеет работать с текстом задачи. Он невнимательно читает условие, не может отделить условие задачи от вопроса, не умеет критически оценить полученный результат.

Развитие способностей решения задач напрямую связано с развитием навыков смыслового и функционального чтения. Ведь чтобы справиться с решением задачи, учащиеся должны:

- осмысленно читать и воспринимать на слух текст задания;

- уметь извлекать и анализировать информацию, полученную из текста;

- уметь критически оценивать данную информацию;

- уметь читать таблицы, диаграммы, схемы, условные обозначения.

Начальный курс математики раскрывается на системе целесообразно подобранных задач. Значительное место занимают в этой системе текстовые задачи. Они необходимы для того, чтобы сформировать у учащихся важные для обыденной жизни знания, а на их базе - умения и навыки, связанные с решением постоянно возникающих проблемных ситуаций.

Я предлагаю вам посмотреть этапы решения текстовых задач и их связь со стратегиями смыслового чтения .

Анализ содержания задачи.

Поиск пути решения задачи.

Составление плана ее решения.

Осуществление плана решения задачи

Проверка решения задачи

Для этого мы организуем определенную систему работы над задачей.

СИСТЕМА РАБОТЫ НАД ЗАДАЧЕЙ

1. Научить детей различать

рассказ литературный и математический.( представляется два варианта текста , из которых ребята выделяют математический рассказ и доказывают свой выбор)

2. Научить различать математический рассказ и задачу

- По рисункам составляем математический рассказ

-чего не хватает чтобы рассказ стал задачей

-что сделать чтобы ответить на вопрос
- решение и ответ

3. Работа с моделью задачи

Работая над каждой задачей мы выделяем каждую ее часть , проговариваем эти части , анализируем , делаем выводы и Отсутствие какой-либо части задачи приводит к общему нарушению структуры задачи. Придумываем и составляем свои задачи .

4. Научить различать текст задачи от условия

На данном этапе ведется работа по содержанию задачи и выделение отличий текста задачи от условия .

Чтобы дети лучше понимали смысл задачи ведется

5. работа со схемами краткой записи задач .

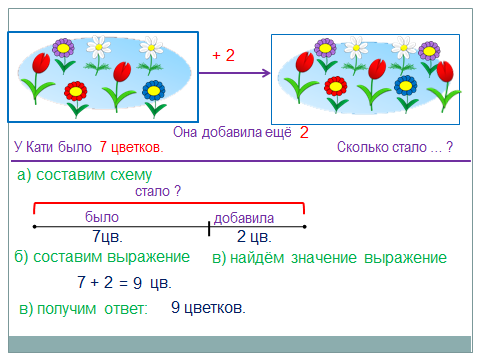
1. По рисунку составляем задачу

2. Проговариваем ее.Выделям части задачи .

3. Составляем схему , обозначаем все на схеме

4. Составляем выражение, находим значение

5. Ответ .

В контексте смыслового чтения при решении задач роль учителя состоит в том, чтобы организовать и направить детей на решение задачи с помощью наводящих вопросов, научить выделять и находить «главные» слова. Это возможно при помощи диалога и в нем участвуют все дети.

Прием: Тонкие и Толстые вопросы.

Тонкие вопросы- вопросы, требующие простого, односложного ответа.

Толстые вопросы- вопросы, требующие подробного, развернутого ответа.

Прием “Ключевые слова”

Стадию вызова на уроке можно осуществить многими методами, в том числе и хорошо известными, например, "ключевые слова", по которым можно придумать рассказ или расставить их в определенной последовательности, а затем, на стадии осмысления искать подтверждение своим предположениям, расширяя материал.

Например, Закрепление знаний по опорным словам при изучении величин ( времени, массы, площади, длины).

Прием “Лови ошибку”

Учитель заранее подготавливает текст, содержащий ошибочную информацию, и предлагает учащимся выявить допущенные ошибки.

Важно, чтобы задание содержало в себе ошибки 2 уровней:

• явные, которые достаточно легко выявляются учащимися, исходя из их личного опыта и знаний;

• скрытые, которые можно установить, только изучив новый материал.

Учащиеся анализируют предложенный текст, пытаются выявить ошибки, аргументируют свои выводы. Затем изучают новый материал, после чего возвращаются к тексту и исправляют те ошибки, которые не удалось выявить в начале урока.

Например: задачи с ошибками, с неверной информацией.

На стадии вызова наиболее часто используется ( слайд 5) приём

«Верные, неверные утверждения»: учитель зачитывает верные и неверные утверждения, учащиеся выбирают «верные утверждения» из предложенных, обосновывая свой ответ.

Например, при устном счете

-  Произведение 0 и 9 равно 9;

- Сумма 36 и 14 больше 40;

- Разность 80 и 15 меньше разности 80 и 25.

            На стадии рефлексии после изучения нового материала учитель снова возвращает детей к вопросам. Например, при введении понятия

« Площадь прямоугольника» на стадии вызов повторяем  свойства прямоугольника через игру "Да - нет"

- Через точку можно провести только одну прямую (нет).

- Прямоугольник - это замкнутая ломаная линия (да).

- Прямоугольник - это четырёхугольник, у которого все стороны равны (нет).

- Треугольник, у которого две стороны имеют равную длину, называется равнобедренным (да).

- Треугольник, у которого один угол острый, называется тупоугольным (нет).

- Площадь - это сумма длин сторон прямоугольника (нет)    

Прием составления краткой записи задачи

Автобус едет 3 часа со скоростью 40 км/ч. Какое расстояние проедет автобус за это время?

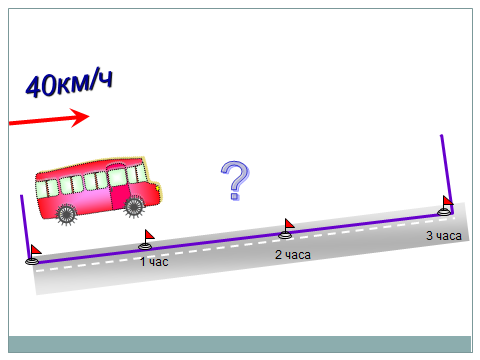
Краткая запись помогает осмыслить задачу, увидеть пути решения

Прием Кластер (Поиск пути решения задачи )

Пользуемся алгоритмом , что тоже помогает осмыслить задачу.

Уверена, что приемы смыслового чтения, используемые на уроках математики в начальной школе для решения текстовых задач, вовлечение учащихся в процесс активной деятельности на уроках поможет детям повысить уровень мотивации, уровень сформированности метапредметных УУД учащихся в лучшую сторону, что впоследствии положительно скажется на качестве математического образования.

.

Литература

1. Федеральный государственный образовательный стандарт начального общего образования // [Электронный ресурс] http://standart edu.ru/catalog.aspx?CatalogId=959.

2. Примерная основная образовательная программа начального общего образования. – М. : Просвещение, 2009. – 201 с.

3. Бондаренко Г. И. Развитие умений смыслового чтения в начальной школе / Г. И. Бондаренко // Начальная школа плюс: до и после // Электронный ресурс www.school 2100.ru