Формула бинома Ньютона. Свойства биноминальных коэффициентов.
Слово бином означает «Два числа». В математике биномом называют «формулу для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных».
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a + b)2 = a2 + 2ab + b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3
Возведение двучлена a + b в степень n может быть произведено по формуле называемой разложением бинома Ньютона.
Бином Ньютона – формула разложения произвольной натуральной степени двучлена в многочлен.
Запишем формулу Ньютона
(a + b)n =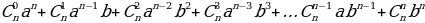
Числа 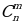 являются биноминальные коэффициентами.
являются биноминальные коэффициентами.
Биномиальные коэффициенты для различных n удобно представлять в виде таблицы, которая называется арифметический треугольник Паскаля. В общем виде треугольник Паскаля имеет следующий вид:
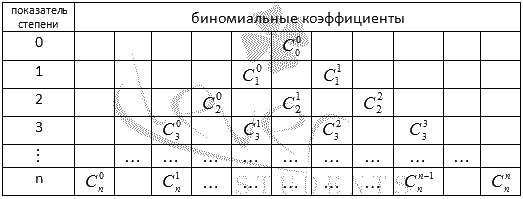
Треугольник Паскаля чаще встречается в виде значений коэффициентов бинома Ньютона для натуральных n:
| показатель степени | Биноминальные коэффициенты |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 1 |
|
|
|
|
|
|
|
|
|
|
| 1 | 1 | 1 |
|
|
|
|
|
|
|
|
|
| 2 | 1 | 2 | 1 |
|
|
|
|
|
|
|
|
| 3 | 1 | 3 | 3 | 1 |
|
|
|
|
|
|
|
| 4 | 1 | 4 | 6 | 4 | 1 |
|
|
|
|
|
|
| 5 | 1 | 5 | 10 | 10 | 5 | 1 |
|
|
|
|
|
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 |
|
|
|
|
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 |
|
|
|
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 |
|
|
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 |
|
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
Боковые стороны треугольника Паскаля состоят из единиц. Внутри треугольника Паскаля стоят числа, получающиеся сложением двух соответствующих чисел над ним. Например, значение десять (выделено красным) получено как сумма четверки и шестерки (выделены голубым). Это правило справедливо для всех внутренних чисел, составляющих треугольник Паскаля, и объясняется свойствами коэффициентов бинома Ньютона.
Пример:
Разложить выражение (a + b)5, используя формулу бинома Ньютона.
Смотрим на строку треугольника Паскаля, соответствующую пятой степени. Биномиальными коэффициентами будут числа 1, 5, 10, 10, 5, 1. Таким образом, имеем формула.
(a + b)5 = a5 + 5 a4 b + 10 a3 b2 + 10 a2 b3 + 5 ab4 + b5
Свойства бинома Ньютона
Задание:
Изучить конспект или презентацию по теме урока и ответить на вопросы (письменно):
1. Понятие бинома.
2. Формула бинома Ньютона (бином Ньютона).
3. Биноминальные коэффициенты.
4. Треугольник Паскаля.
5. Разложить выражение (a + b)10, используя формулу бинома Ньютона.







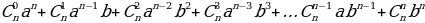
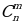 являются биноминальные коэффициентами.
являются биноминальные коэффициентами.



















