Формула корней квадратного уравнения

Формула корней квадратного уравнения

Понятие квадратного уравнения

• Квадратное уравнение — это ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.

Есть три вида квадратных уравнений:

• не имеют корней;
• имеют один корень;
• имеют два различных корня.

0, есть два различных корня. " width="640"

• Чтобы определить, сколько корней имеет уравнение, нужно обратить внимание на дискриминант. Чтобы его найти, берем формулу: D = b2 − 4ac . А вот свойства дискриминанта:
• если D
• если D = 0, есть один корень;
• если D 0, есть два различных корня.

• Квадратное уравнение может быть приведенным или неприведенным — все зависит от от значения первого коэффициента.
• Приведенное квадратное уравнение — это уравнение, где старший коэффициент, тот который стоит при одночлене высшей степени, равен единице.
• Неприведенным называют квадратное уравнение, где старший коэффициент может быть любым.
• Каждое неприведенное квадратное уравнение можно преобразовать в приведенное, если произвести равносильное преобразование — разделить обе его части на первый коэффициент.

Полные и неполные квадратные уравнения

• В определении квадратного уравнения есть условие: a ≠ 0 . Оно нужно, чтобы уравнение ax2 + bx + c = 0 было именно квадратным. Если a = 0, то уравнение обретет вид линейного: bx + c = 0.
• Что касается коэффициентов b и c, то они могут быть равны нулю, как по отдельности, так и вместе. В таком случае квадратное уравнение принято назвать неполным.

• Неполное квадратное уравнение — это квадратное уравнение вида ax2 + bx + c = 0, где оба или хотя бы один из коэффициентов b и c равен нулю.
• Полное квадратное уравнение — это уравнение, у которого все коэффициенты отличны от нуля.

Решение неполных квадратных уравнений

• Начнем с решения неполных квадратных уравнений, в которых b и c равны нулю, то есть, с уравнений вида ax2 = 0.
• Уравнение ax2 = 0 равносильно x2 = 0. Такое преобразование возможно, когда мы разделили обе части на некое число a, которое не равно нулю. Корнем уравнения x2 = 0 является нуль, так как 02 = 0. Других корней у этого уравнения нет, что подтверждают свойства степеней.
• Таким образом, неполное квадратное уравнение ax2 = 0 имеет единственный корень x = 0.

Пример

Решить −6x2 = 0.

Как решаем:

Замечаем, что данному уравнению равносильно x2 = 0, значит исходное уравнение имеет единственный корень — нуль.

По шагам решение выглядит так:

− 6x2 = 0

x2 = 0

x = √0

x = 0

Ответ : 0.

0, то корни уравнения x2 = - c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = - c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = - c/а. " width="640"

Обратим внимание на неполные квадратные уравнения вида ax2 + c = 0 , в которых b = 0, c ≠ 0.

• перенесем c в правую часть: ax2 = - c,
• разделим обе части на a: x2 = - c/а.

Если — c/а

Если — c/а 0, то корни уравнения x2 = - c/а будут другими. Например, можно использовать правило квадратного корня и тогда корень уравнения равен числу √- c/а, так как (√- c/а)2 = - c/а. Кроме того, корнем уравнения может стать -√- c/а, так как (-√- c/а)2 = - c/а.

Пример

Найти решение уравнения 8x2 + 5 = 0.

Как решать:

Перенесем свободный член в правую часть:

8x2 = - 5

Разделим обе части на 8:

x2 = - 5/8

В правой части осталось число со знаком минус, значит у данного уравнения нет корней.

Ответ : уравнение 8x2 + 5 = 0 не имеет корней.

Неполное квадратное уравнение ax2 + bx = 0 можно решить методом разложения на множители. Разложим на множители многочлен, который расположен в левой части уравнения — вынесем за скобки общий множитель x. Теперь можем перейти от исходного уравнения к равносильному x * (ax + b) = 0. А это уравнение равносильно совокупности двух уравнений x = 0 и ax + b = 0, последнее — линейное, его корень x = −b/a.

Таким образом, неполное квадратное уравнение ax2 + bx = 0 имеет два корня:

• x = 0;
• x = −b/a.

Пример

Решить уравнение 0,5x2 + 0,125x = 0

Как решать:

Вынести х за скобки

х(0,5x + 0,125) = 0

Это уравнение равносильно х = 0 и 0,5x + 0,125 = 0.

Решить линейное уравнение:

0,5x = 0,125,

х = 0,125/0,5

Разделить:

х = 0,25

Значит корни исходного уравнения — 0 и 0,25.

Ответ : х = 0 и х = 0,25.

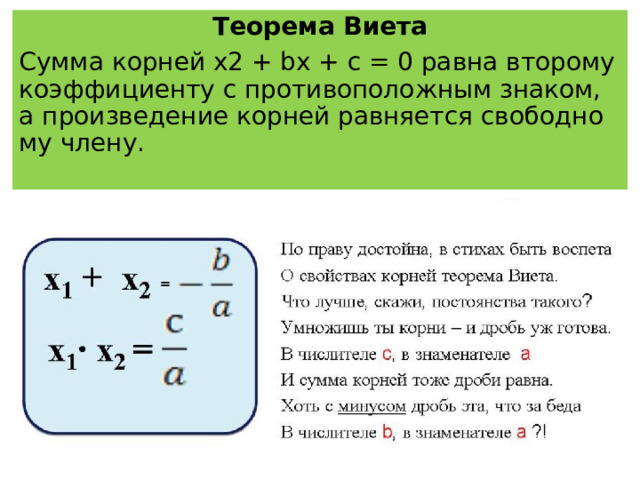
Теорема Виета

Сумма корней x2 + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение корней равняется свободному члену.

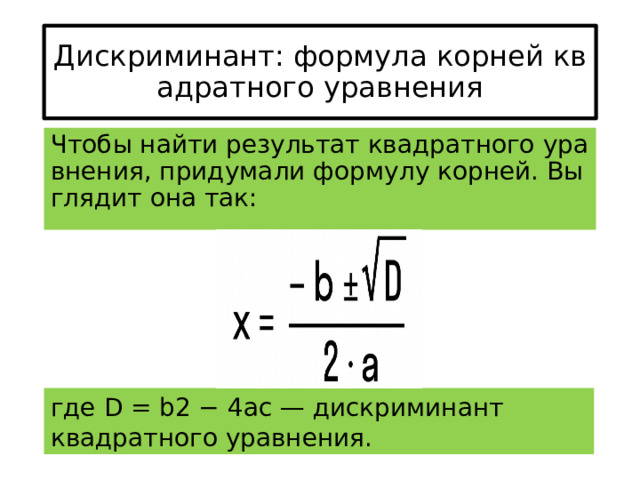
Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Алгоритм решения квадратных уравнений по формулам корней

• Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.
• В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения. Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней.

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b2−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = - b2/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Пример

Решить уравнение −4x2 + 28x — 49 = 0.

Как решаем:

Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0

Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень

Найдем корень

х = - 28/2(-4)

х = 3,5

Ответ : единственный корень 3,5.

Пример

Решить уравнение 3x2— 4x+94 = 0.

Как решаем:

Найдем дискриминант по формуле

D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

Дискриминант отрицательный, поэтому корней нет.

Ответ : корней нет.