Просмотр содержимого документа
«Формула корней квадратного уравнения.»
Урок алгебры в 8классе.
Тема: Формула корней квадратного уравнения.
Цели:
Вывести формулу для вычисления дискриминанта и формулу для вычисления корней квадратного уравнения.
Выработать навык решения квадратных уравнений по формуле.
Учащиеся должны убедиться ,что они открыли новый универсальный способ для решения квадратных уравнений.
Повторение:
Решите уравнения
Х2=0,49 2х2=72 3х2-5х=0
Х1=-0,7 х2=0,7 х2=36 х(3х-5)=0
Х1=6 х2=-6 х1=0 х2=
Х2+10х+25=0 х2+4х+3=0
(х+5)2=0 (х2+4х+4)-4+3=0
Х=-5 (Х+2)2-1=0
(х+2-1)(х+2+1)=0
х =-1 х=-3
Каким способом решили полные квадратные уравнения?
( Способом выделения квадрата двучлена).
Новая тема.
Выделим квадрат двучлена из квадратного трехчлена ах2+вх+с=0
Ах2+вх+с=0 (:а)
Х2+ х+
х+ =(х2+2
=(х2+2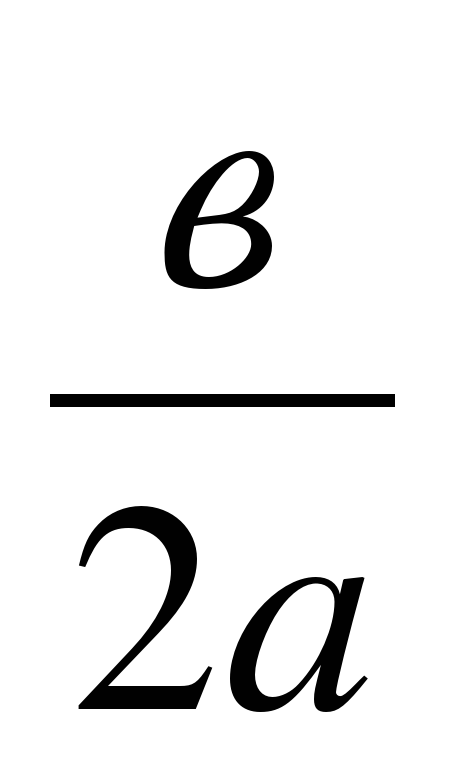 х+
х+ )-
)- +
+ =(х+
=(х+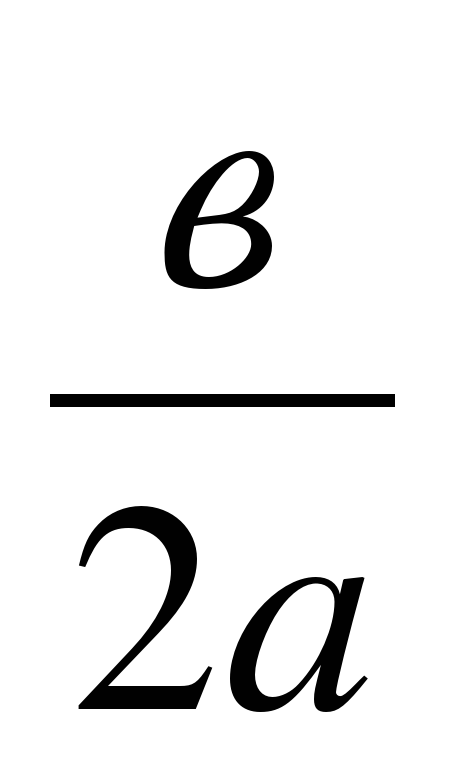 )2-
)2- ;
;
Выражение в2-4ас=Д , где Д-дискриминант.
1. Если Д  0 , то
0 , то
находим корни по формулам: х1=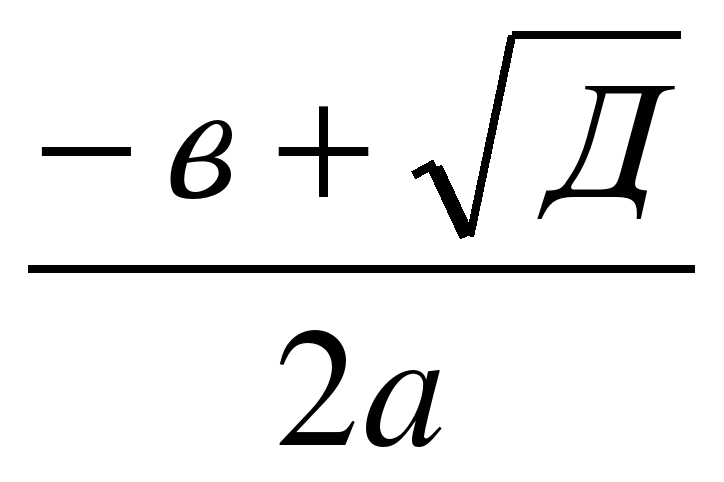 х2=
х2=
если Д=0, то корни находим 
по формуле х = -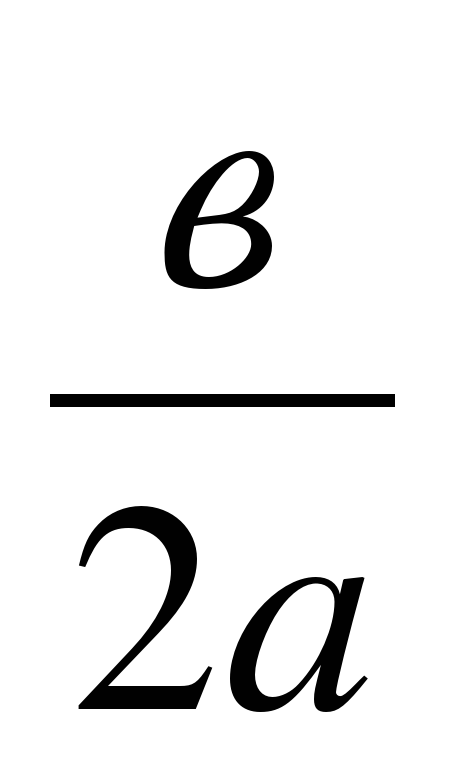
если Д 0 то уравнение не имеет корней.
0 то уравнение не имеет корней.
Практическая часть.
Решите уравнения
1)12х2+7х+1=0 Д=72-4·12·1=1 , Д 0
0
Применим формулу корней квадратного уравнения
Х=
Ответ : х1=- , х2=-
, х2=- .
.
х2-12х+36=0
Д=(-12)2-4·1·36=0
Х= =6 Ответ: х=6.
=6 Ответ: х=6.
7х2-25х+23=0
Д=(-25)2-4·7·23=625-644=-19, Д 0.
0.
Ответ: уравнение не имеет корней.
Для квадратных уравнений, у которых второй коэффициент является четным числом, формулу корней удобно записать в другом виде.
Рассмотрим квадратное уравнение ах2+2кх+с=0
Найдем Д=4к2-4ас=4(к2-ас)
Очевидно, что число корней уравнения зависит от знака выражения к2-ас. Обозначим это выражение через Д1.
Если Д1≥0, то по формуле корней квадратного уравнения получим , что
Х=
 , т.е. х=
, т.е. х= , где
, где
Д=к2-ас.
Если Д 0 , то уравнение не имеет корней.
0 , то уравнение не имеет корней.
Закрепление.
Решите уравнение:9х2-14х+5=0
Д=(-7)2-9·5=49-45=4
Х=; х1=1 ; х2=
Ответ: х1=1; х2=.
Домашнее задание. №533(а, б); №534.

















