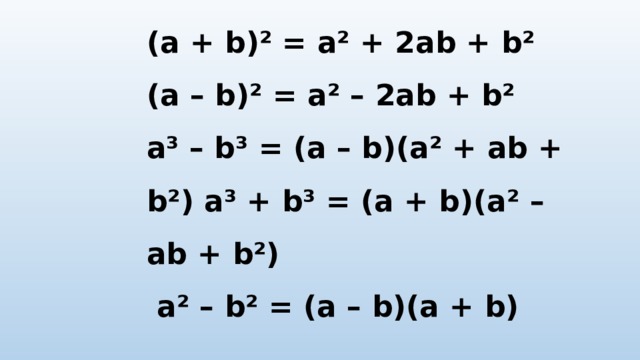Формулы сокращенного умножения

« Кто не уважает прошлого,

тот лишен будущего»

ФОРМУЛЫ

СОКРАЩЕННОГО

УМНОЖЕНИЯ

Заполните пропуски в формулах:

(а +…) 2 = … + 2аb + … ;

(а … b) … = а 2 – 2аb + … ;

а 3 - … = (а – b)(… + аb + …);

а 3 + b 3 = (… …)(а 2 … + b 2 );

а 2 – b 2 = (… b)(а – …).

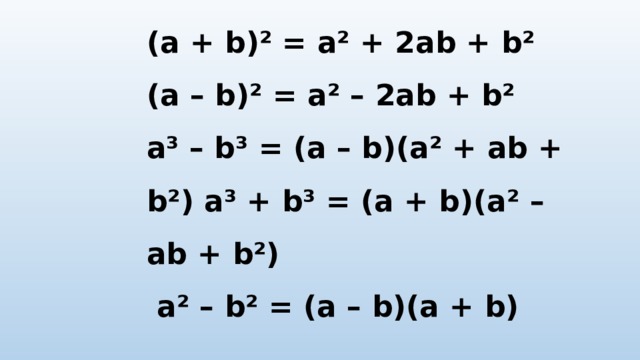
(a + b)² = a² + 2ab + b² (a – b)² = a² – 2ab + b² a³ – b³ = (a – b)(a² + ab + b²) a³ + b³ = (a + b)(a² – ab + b²) a² – b² = (a – b)(a + b)

Математическое домино

7 февраля 279-я стрелковая дивизия овладела Острой Могилой в районе Ворошиловграда, продолжая совместно со 2-м танковым корпусом бои на южной окраине города, и отражая непрерывные контратаки противника.

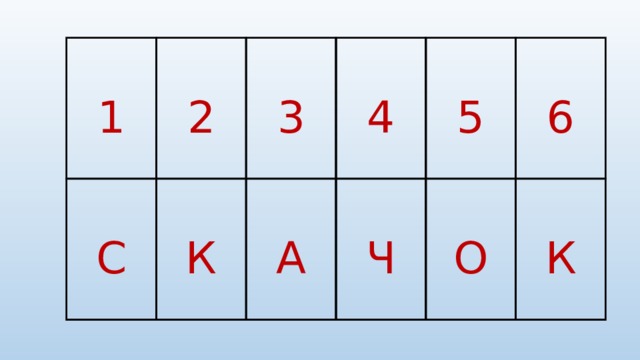
Установи соответствие

1

(a + 3) 2 =

2

(x 2 – 2x + 4)(x + 2) =

А

3

x 2 -1

О

(x - 1)(x + 1) =

4

(2 - y) 2 =

b 3 -1

Ч

5

6

(b - 1)(b 2 + b + 1) =

4-4у+y 2

К 1

x 3 +8

(x 2 - 1)(1 + x 2 ) =

С

а 2 +6а+9

К 2

x 4 - 1

1

2

С

3

К

4

А

5

Ч

6

О

К

Ворошиловградская операция — наступательная операция войск Юго-Западного фронта в Великой Отечественной войне, проведенная 29 января — 18 февраля 1943 года. Также известна под кодовым наименованием операция «Скачок».

Верно-неверно

№

1

2

Верно/неверно

(x+3)(x 2 -3x+9)=x 3 +27

3

(b+a)(a-b)=b 2 -a 2

балл

4

x 2 +6ax+9a 2 =(x+3a) 2

5

4a 2 -9=(2a+3)(3-2a)

(x-8) 2 =x 2 +16x+64

ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО

• Пусть a и b — положительные числа. Рассмотрим квадрат со стороной a+b и вырежем в двух его углах квадраты со сторонами a и b. Площадь квадрата со стороной a+b равна (a+b)²
• Этот квадрат мы разрезали на 4 части: квадрат со стороной a (его площадь a²), квадрат со стороной b (его площадь b²), 2 прямоугольника со сторонами a и b (площадь каждого прямоугольника равна ab)
• Значит, (a + b)² = a² + b² + 2ab

11 февраля в боях за подступы к Ворошиловграду войска 3-й гвардейской армии (командующий Д. Д. Лелюшенко) добились существенных успехов. 59-я гвардейская и 279-я стрелковые дивизии предприняли серию атак на Ворошиловград. К исходу дня бои шли на станции Вергунка, юго-западной, южной и юго-восточной окраинах города.

Физкультминутка

(a + b)²=

(х - у)(х + у) =

(х - у) 2 =

(х - у)(х 2 + ху + у 2 )=

(х + у)(х 2 – ху + у 2 )=

В течение 11 февраля были заняты либо выведены из строя станции Ольховка, Успеновка, Иллирия, Селезнёвка, захвачены сёла Георгиевка и Лутугино. На станции Ольховка было захвачено 7 паровозов и 2 эшелона с заводским оборудованием.

При использовании формул

квадрата суммы или квадрата разности учитывайте, что

( ─a — b)² = (a + b)²;

(b — a)² = (a — b)².

Это следует из того, что (-а)² = а²

Некоторые математические фокусы

Отметим, что на формулах квадрата суммы и квадрата разности основаны некоторые математические фокусы, позволяющие производить вычисления в уме. Например, можно практически устно возводить в квадрат числа, оканчивающиеся на 1, 2, 8 и 9.

71 ² = (70 + 1)² = 70² + 2·70·1 + 1² = 4900 + 140 + 1 = 5041

Но самый элегантный фокус связан с возведением в квадрат чисел, оканчивающихся цифрой 5:

85² = (80 + 5)² = 80² + 2·80·5 + 5² = 80·(80 + 10) + 25 = 80·90 + 25 = 7200 + 25 = 7225

.

Вычислить удобным способом

165 2 -65 2

34 2 +2∙34∙36+36 2

Вычислить удобным способом

165²-65²=(165-65)(165+65)= 100 ∙ 230= 23000

34²+2∙34∙36+36²=(34+36)²=70²= 4900

Реши уравнение

• (x+6)²-(x-5)(x+5)=73
• х 2 +2х+1=0
• х 2 -25=0
• х 3 -х=0

60-я стрелковая дивизия заняла Александровку северо-западнее Ворошиловграда, охватывая город с севера. 4-я гвардейская мотострелковая дивизия и 4-я гвардейская танковая бригада 2-го гвардейского танкового корпуса заняли Лутугино на южных подступах к Ворошиловграду.

8-й кавалерийский корпус силами 21-й кавалерийской дивизии 13 февраля овладел станцией Мануиловка и наступал вдоль железной дороги Ворошиловск — Дебальцево, производя подрывы железнодорожного полотна

УСПЕХ

9,9 2

На рассвете 14 февраля советские войска после 40-минутной артподготовки пошли в общую атаку на Ворошиловград. В 8:25 части 18-го стрелкового корпуса ударили с юга и востока, овладев юго-восточной частью города. На высоких скоростях в город вошли танковые бригады, которые были встречены артогнём немецких фаустников. При прорыве вражеской обороны в городе погибли комбриги М. И. Городецкий и А. П. Коденец, начальник штаба корпуса С. П. Мальцев. В результате непродолжительного боя, оборона противника была прорвана, последний начал отход на запад. На плечах отступающих в центральную часть Ворошиловграда ворвалась пехота. К исходу дня большая часть города была в руках наступающих.

Балл

Оценка

0-2

1

3-5

2

6-14

15-24

3

4

25-27

5

Домашнее задание

на «5» - стр. 177, №№ 8,9,10

на «4» - стр. 177, №№ 5,6,7

на «3» - стр. 177, №№1,2,3,4

рефлексия

  Как найти квадрат числа, оканчивающегося на 5?

Быстрый счет