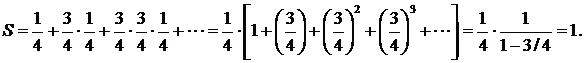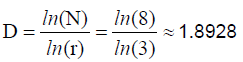Фрактал
Определение фрактала, дано Мандельбротом: "Фракталом называется структура, состоящая из частей, кот в каком-то смысле подобны целому".
Применение фракталов
- Генерация изобр природ объектов: Фрактальное дерево Фракталы примен для получ изобр деревьев, кустов, берег линий при построении ландшафтов, поверхности морей, карт раскраски.
- Механика жидкостей Фракталами хор опис след процессы, отн к механ жидк и газов: динамика и турбулентн сложных потоков; моделир пламени; изуч пористых м-лов, в т ч в нефтехи.
- Биология Моделир популяций; биосенсорн взаимод; процессы внутри орг-ма, напр, биение сердца.
-Фрактальные антенны к приёмнику. Оказ, что такая антенна раб не хуже обыч. И хотя физ принципы работы такой антенны не изуч до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск
При моделировании пористых материалов (в нефтехимии) также используют фракталы
Классификация фракталов
В осн фракталы делят на: геометрические, алгебраические, стохастические. но есть и другие классиф: Рукотворные и природные. К рукотворным относят те фракталы, кот придуманы учёными, они при любом масштабе обладают фрактальными св-вами. На природные фракталы накл огранич на обласати существ — т е макс и мин размер, при кот у объекта наблюдают фрактальные свойства
Построение простейших фракталов.
Геометрические фракталы: Фракталы этого класса самые наглядн. В двухмерн сл их получ с пом нек ломаной (или поверхности в трехмерн сл), наз генератором. За 1 шаг алг каждый из отрезков, соста ломаную, заменя на ломаную-генератор, в соотв масштабом В рез беск повтор этой проц, получ геометрич фрактал
Кривая Коха — фрактальная кривая, непрерывна.
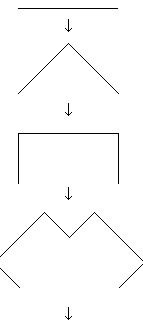
Три копии кривой Коха, постр (остриями наружу) на сторонах правильного треугольника, обр замкн кривую, наз снежинкой Коха. Кривая Коха задается такой системой итерационных функций
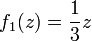
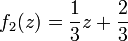
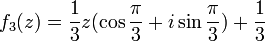
Снежинка рис рекурсив обр. Снач она выглядит как треуг. Затем на сторонах этого треуг рисуют треуг выступы. Получа 6конеч звезда. На сторонах этой звезды снова рис треуг выступы (см. синюю фигуру). Процесс наращив треуг выступов м продолж до беск и получ в пределе вп корректно опред множество точек на плти.В матем, в отл от прогр, доп такие беск рекурсивные определения.
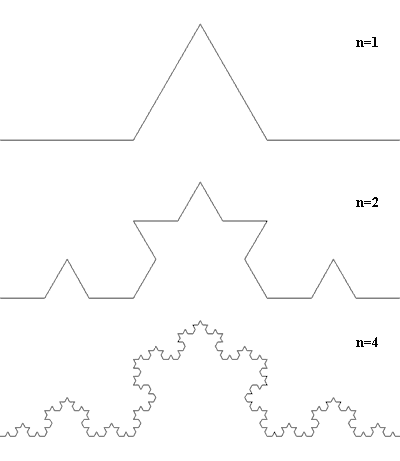
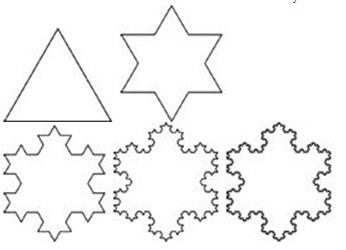
Рис.1. Построение триадной кривой Коха.
На каждом шаге у нас получ нек обычная фигура (не фрактал), а в пределе (после беск числа шагов) получ фрактал. Если полож, что длина стороны исх треуг=1, то длина стороны 6уг звезды=1/3. Длина стороны след фигуры ещё в 3 раза меньше, т е1/9. М запис общую ф=лу: 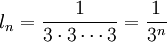 . Зам, что число сторон mn растёт от ном шага как
. Зам, что число сторон mn растёт от ном шага как 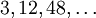 , то есть
, то есть 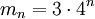 . Периметр Pn фигуры, получ на шаге n, есть произв числа сторон на длину:
. Периметр Pn фигуры, получ на шаге n, есть произв числа сторон на длину: 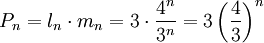 . Таким обр,
. Таким обр, 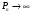 Площадь под кривой, если принять площадь первого образующ треуг за 1:
Площадь под кривой, если принять площадь первого образующ треуг за 1:
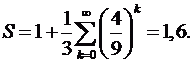
Задача. Пусть две вершины нач правильн треугольника лежат в точках (0;0) и (1;0). Какие ещё есть точки с рац координатами, принадлежащие снежинке Коха?
Множество Кантора
Классич мн-во Кантора или пыль Кантора, Это мн-во изв как прим мн-ва 0-меры Лебега, чья мощн=мощн континуума c.Постр классич пыли Кантора нач с выбрас средней трети (не вкл концы) ед отрезка. Т е исх мн-во есть отр [0,1], и 1 шаг состоит в удал откр инт=ла (1/3, 2/3). На след и всех ост шагах выкид сред треть (не вкл концы) всех отрезков тек уровня. Таким обр, получ посл-ть мн=в рис 1
.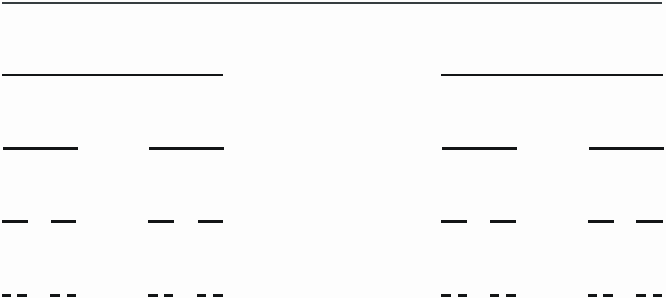 Рис.1
Рис.1
C0 = [0, 1] C1 = [0, 1/3] È [2/3, 1] C2 = [0, 1/9] È [2/9, 1/3] È [8/9, 1]
Предельное мн-во C, кот предст собой пересеч мн-в Cn, n = 0, 1, 2, …, наз классич мн-вом Кантора или пылью Кантора Выч фракталь размер этого мн-ва. Восп ф-лой (1). Оч, что на n-м шаге постр 2n отрезк длины 1/3n кажд. Поэтому в кач N(e ) на этом шаге м взять вел 2n, а в кач e — вел 1/3n. Предел e à 0 соотв пределу n à ¥ . Поэтому фрактальная размерн равна
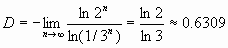 Она оказ меньше Евклид размерн пр-ва, в кот распол это мн=во (т.е. его длина =0), но отлична от нуля, т.е. больше топологич размерн элементов (точек) этого множества.
Она оказ меньше Евклид размерн пр-ва, в кот распол это мн=во (т.е. его длина =0), но отлична от нуля, т.е. больше топологич размерн элементов (точек) этого множества.
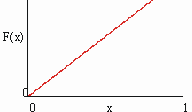
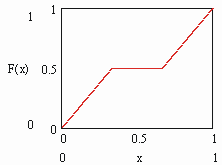
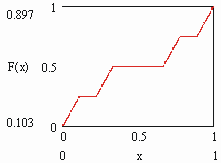
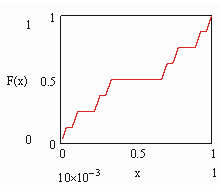
Сущ функциональный аналог мн-ва Кантора — функция кантора. Распр равном на C ед массу (меру) с плотн m . Тогда функц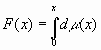 опис распред меры на канторов носит. Она явл непрер возр функц, кот тем не м почти всюду имеет 0- произв (т.е. гориз). Её наз “чёртовой лестниц” (рис.2).
опис распред меры на канторов носит. Она явл непрер возр функц, кот тем не м почти всюду имеет 0- произв (т.е. гориз). Её наз “чёртовой лестниц” (рис.2).
Салфетка Серпинского 1 фрактал созд чел мозаика на полу англ церкви 1104 г
Исх мн-вом, соотв 0- шагу, явл равностор треуг (рис. 63). Затем он разбив
на 4 обл путем соед сер сторон исх треуг отр прямых. Затем удал внутр центр обл исх треуг – малый
внутр «переверн треуг». Затем, на след шаге итерации, этот процесс повт для каждого из 3 оставш треуг. Продол опис проц до беск, обра мн-во, наз салфеткой Серпинского.
Оч, фрактальная размерн салфетки Серпинского: 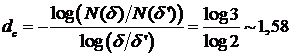
 Первые шаги алг постр салфетки Серпинского
Первые шаги алг постр салфетки Серпинского
Этот фрактал интер тем, что занима им площадь=0. Для обосн этого подсч сумм площ частей, искл при постр. На 1 шаге выбрас 4я часть площади исх треуг, на 2м шаге у каждого из 3 треуг удал 4я часть площади и т.д. Таким обр, полная удаленная площадь вычисляется как сумма ряда:
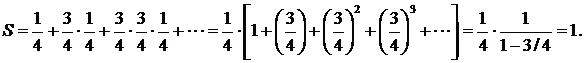
ковер Серпинского
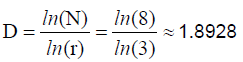
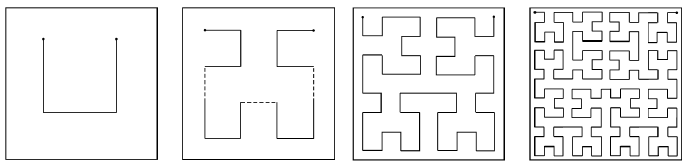
Самоподобная кр Гилберта проходит всюдц плотно заполняет обл квадрата
Для постр кривой Леви на 0- шаге н взять отр АВ произв длины. 1й шаг вкл постр равнобедр прямоуг треуг с отр АВ в кач гипотенузы. При этом сама гипотенуза в дальн постр не участв и искл из кривой. Таким обр, 1е покол кривой предст ломан АСВ. На 2 шаге с каждым из отр АС и СВ продел ту же оп, что и с отр АВ на 1 шаг. Послед покол кривой строятся по такому же алг. В рез, получ кривую рис.2
фрактал «Пифагорово дерево».
состоит из подоб эл, кот представляют квадрат, на одной стороне кот нарис прямоуг треуг. На каждом катете треуг стр тот же эл фрактала и таким обр получ дерево Если задать глубину рекурсии 5, то Черепашка нарисует вот такое пифаг дерево. Здесь в каждом направл 5 исходных элементов.
Если взять треугольник не равнобедренный, а например, с углами 300 и 600, то стороны находим как р*Cos 30 и p*Cos 60. Пифагорово дерево примет вид:
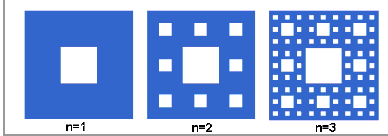
Губка Менгера
Размерность фракталов
С математической т зрения фракталы – множества с дробной рзмерностью
Фрактальная размерность D (метрическая мера введена Хаусдорфом) показыв, наск плотно и равном эл данного мн=ва заполняют евкл пр=во
Гетерогенная химия –химия на границе раздела фаз.
Химическася реакция определяется не только химическим и физическим составом но и геометрией
Наиб наглядный метод определения D основан нас прямом вычислении производящей функции. определение длины фрактальной линии -ее покрывают набором квадратов со стороной
и при разных  считают число Затем строят зависимость и по углу наклона находят фрактальную размерность
считают число Затем строят зависимость и по углу наклона находят фрактальную размерность
или
N - кол уменьшенных в r раз копий, необходимых для заполнения исходного объекта (или будем измерять объект уменьшенной линейкой 
Размерность подобия :
или для Евклид объектов, выр целым (1,2,3), что совп с топологич размерн
Фрактальная размерность не зависит от масштаба рассмотрения
Другой геометрический метод –из соотношений между свойствами множеств разной геометрической размерности. Наспример если для фигуры ограниченной фрактальной границей измерить площадь  и длину
и длину  где R характерный размер то из следует
где R характерный размер то из следует
откуда фрактальная размерность границы D =танг угла наклона лог кв периметра от лог ограниченной площади. При этом длину периметра измеряют либо непосредственно (курвиметром) либо так же как в задаче о фрактальной линии
Недостаток –эмпирический подбор  Более надежны методы прямого экспериментального определения По большому количеству одинаковых фрактальных класатеров нас фотоплаастинке
Более надежны методы прямого экспериментального определения По большому количеству одинаковых фрактальных класатеров нас фотоплаастинке
Пропуская световой поток толщины r и измеряя интенсивность I прошедшего света м исп ф-лу
Литература
1)Шмидт Ф.К. Фракталы в физической химии гетерогенных систем
2) В. К. Балханов Основы фрактальной геометрии и фрактального исчисления,
инст Физического мастериаловедения Сиб РАН, Улан-УДЭ, 2013
3) ФРАКТАЛЫ И ИХ ПРИКЛАДНОЙ АСПЕКТ КГТУ, 2006
4)Основы фрактальной геометрии, https://studylib.ru









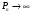 Площадь под кривой, если принять площадь первого образующ треуг за 1:
Площадь под кривой, если принять площадь первого образующ треуг за 1:  Рис.1
Рис.1 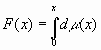 опис распред меры на канторов носит. Она явл непрер возр функц, кот тем не м почти всюду имеет 0- произв (т.е. гориз). Её наз “чёртовой лестниц” (рис.2).
опис распред меры на канторов носит. Она явл непрер возр функц, кот тем не м почти всюду имеет 0- произв (т.е. гориз). Её наз “чёртовой лестниц” (рис.2).



 Первые шаги алг постр салфетки Серпинского
Первые шаги алг постр салфетки Серпинского