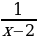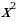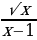Функция. Область определения и область значений функции.

Тема урока: Функция. Область определения и область значений функции

Тип урока: Урок изучения нового материала

Продолжительность: 45 мин

Цель урока: Формирование понятий области определения и области значений функции, развитие умения находить эти множества и применять полученные знания при решении практических задач.

Ход урока:

I. Организационный этап (2 минуты)

— Добрый день, ребята! Садитесь, пожалуйста. Я рада вас видеть бодрыми и готовыми приступить к изучению нового интересного материала. Сегодня мы продолжаем наше путешествие в мир алгебры и познакомимся с важными понятиями, такими как область определения и область значений функции. Эти понятия станут основой нашего дальнейшего изучения многих важных аспектов математики. Давайте начнем урок!

Все готовы? Отлично, приступаем!

II. Актуализация опорных знаний (8 минут)

— Ребята, давайте вспомним некоторые важные моменты, которые нам пригодятся сегодня. Прежде всего, скажите, что такое функция?

Выслушав несколько вариантов ответов, подводит итог:

— Верно, функция — это правило, которое каждому элементу одного множества ставит в соответствие единственный элемент другого множества. Например, зависимость пути от времени, температура воздуха от времени суток и многое другое.

Далее продолжает обсуждение:

— Поднимите руки, кто помнит, как обозначают функцию? Правильно, чаще всего используется запись вида y = f(x). Здесь x — аргумент, y — значение функции.

Затем задаёт ещё несколько вопросов:

— Назовите несколько видов функций, которые мы уже рассматривали раньше. Какие бывают функции?

Предположительно ученики назовут линейную (y=kx+b), квадратичную (y=ax²+bx+c) и обратную пропорциональность (y=k/x). Учитель фиксирует правильные ответы и добавляет:

— Хорошо справились! Теперь переходим непосредственно к нашей сегодняшней теме. Мы рассмотрим две ключевые характеристики каждой функции: область определения и область значений. Для начала попробуем разобраться, что же это значит.

III. Изучение нового материала (20 минут)

1. Понятие области определения функции

— Итак, друзья мои, первым делом поговорим о важной характеристике любой функции — её области определения. Запишите в тетради следующее определение:

«Область определения функции — это множество всех тех значений переменной х, при которых функция существует и принимает конкретные значения».

Проще говоря, это все те числа, которые можно подставить в формулу функции и получить осмысленный результат. Если мы попытаемся поставить какое-то число вне этой области, то функция либо перестанет существовать, либо потеряет смысл.

Давайте разберём это подробнее на примере простой функции:

f(x)=√х​

Что означает квадратный корень из какого-нибудь числа? Очевидно, мы можем извлечь корень только из положительного числа или нуля. Значит, наша функция будет иметь смысл лишь тогда, когда x больше или равен нулю. Следовательно, записываем нашу область определения следующим образом:

D(f)=[0,+∞)

Это читается так: «От нуля до плюс бесконечности включительно». То есть любое положительное число, и ноль мы смело можем подставлять в данную функцию.

Рассмотрим теперь немного сложнее пример:

g(x) =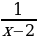

Здесь важно обратить внимание на знаменатель дроби. Вспоминайте, почему нельзя делить на ноль? Потому что такая операция теряет смысл. Значит, уравняем знаменатель к нулю и решим получившееся уравнение:

x−2=0

x=2

Получили, что при x равном двум функция становится неопределённой. Тогда область определения выглядит так:

D(g)=(−∞,2)∪(2,+∞)

Мы исключили точку два, потому что именно там функция терпит разрыв и перестаёт существовать.

Итак, теперь понятно, что область определения показывает нам, какие значения x можно свободно подставлять в функцию, а какие недопустимы. Это важная характеристика каждой функции, которую надо уметь находить.

2. Понятие области значений функции

— Продолжим изучение свойств функций и перейдем ко второй важнейшей характеристике — области значений функции. Запишем определение:

«Область значений функции — это множество всех возможных значений, которые принимает сама функция при всевозможных значениях аргумента (переменной x)».

Другими словами, это тот диапазон, куда попадают все наши вычисленные значения функции.

Возьмем предыдущий пример функции

f(x)=√х​

и посмотрим, какие значения может принимать эта функция. Поскольку квадратный корень извлекается только из положительных чисел и нуля, результатом будет тоже неотрицательное число. Поэтому область значений функции

√x​

ограничится всеми положительными числами и нулём:

E(f)=[0,+∞)

Теперь возьмём другую простую функцию:

h(x)=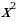

Какой результат получится, если возводить любые числа в квадрат? Ответ очевиден: даже отрицательные числа, возведённые в квадрат, дадут положительные значения. Но поскольку возведение в квадрат любого действительного числа даёт результат не меньше нуля, область значений будет следующей:

E(h)=[0,+∞)

Обратите внимание, область значений иногда проще определить графически, посмотрев на график функции. Посмотрите внимательно на графики некоторых известных функций и постарайтесь сами назвать их области значений.

Итак, запомните главное отличие: область определения — это ограничения на выбор аргументов, а область значений — это границы результата, который получается при применении функции.

3. Способы нахождения областей определения и значений функции

— Чтобы успешно решать задачи на нахождение областей определения и значений функций, полезно освоить несколько методов. Рассмотрим их подробнее.

Самый распространённый способ — это решение неравенства или системы неравенств, исходя из условия существования функции. Вычисляем пределы значений переменных, при которых функция имеет смысл.

Например, если имеем дробь, то нужно убедиться, что знаменатель не равен нулю. Или если функция содержит квадратный корень, то выражение под корнем должно быть неотрицательным.

Иногда удобнее посмотреть на график функции. Именно визуально легче увидеть промежутки изменения аргумента и значений функции. Особенно этот способ полезен для сложных выражений или ситуаций, когда точное аналитическое решение затруднено.

Например, взглянув на график функции

y=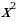 , сразу видно, что область значений лежит в пределах от нуля и выше.

IV. Закрепление изученного материала (10 минут)

Выполнить упражнения вместе с учениками, разобрав несколько примеров:

1. Практикум

Чтобы лучше усвоить методы, применим оба способа на конкретных примерах:

Пример 1.Определим область определения функции

f(x)= ​​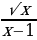

Сначала найдем корни выражения под корнем и исследуем знаменатель. Далее сделаем вывод.

Пример 2.Используя график, найдём область значений функции

h(x)=∣x∣

Обратите внимание, какие значения принимает модуль абсолютной величины.

Работайте активно, задавайте вопросы, если возникнут сомнения или недопонимания. Чем точнее вы научитесь определять области определения и значений, тем успешнее будете справляться с последующими задачами алгебры.

2. Задание из учебника

V. Итог урока (3 минуты)

— Ну что ж, дорогие мои, подошло к концу наше занятие. Давайте коротко подведём итоги сегодняшнего урока.

Сегодня мы узнали:

• Что такое область определения функции, как её искать, и зачем она важна.

• Что представляет собой область значений функции и как правильно указывать её границы.

• Рассмотрели два метода поиска этих характеристик: аналитический и графический.

Какие выводы сделали? Что оказалось трудным? Были ли моменты, вызвавшие затруднения?

Помните, что повторение — мать учения. Постарайтесь дома повторить пройденное, решить дополнительные задачи, проверить себя самостоятельно.

Ну и наконец, оцениваю вашу работу на уроке. Молодцы, работали хорошо, были внимательны и активны. Спасибо большое за ваш интерес и старания.

VI. Домашнее задание (2 минуты)

Записать домашнее задание:

§1, упражнения №3, 11, 16