§ 1. Функции и их свойства.
п. 1. Функция. Область определения и область значений функции.
Функцией  называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции).
называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции).
Например,  .
.
Каждая функция имеет область определения и область значений. Разберёмся, что это такое.
Областью определения функции  называется множество всех значений, которые может принимать независимая переменная х (аргумент). Обозначается она так:
называется множество всех значений, которые может принимать независимая переменная х (аргумент). Обозначается она так: 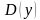 .
.
Например, рассмотрим функцию 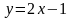 . Нам нужно определить, какие значения может принимать х. Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, областью определения функции является любое число, т.е.
. Нам нужно определить, какие значения может принимать х. Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, областью определения функции является любое число, т.е. 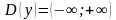 .
.
Рассмотрим теперь функцию 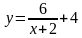 . Здесь мы замечаем, что х находится в знаменателе, а всем известно, что на 0 делить нельзя. Поэтому, мы находим число, при котором знаменатель станет равным 0. Это число
. Здесь мы замечаем, что х находится в знаменателе, а всем известно, что на 0 делить нельзя. Поэтому, мы находим число, при котором знаменатель станет равным 0. Это число 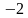 . Значит, х может принимать любые значения, кроме
. Значит, х может принимать любые значения, кроме 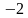 . Поэтому, областью определения данной функции является любое число, кроме
. Поэтому, областью определения данной функции является любое число, кроме 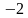 , т.е.
, т.е. 
Областью значений функции  называется множество всех значений, которые может принимать зависимая переменная у (значение функции). Обозначается она так:
называется множество всех значений, которые может принимать зависимая переменная у (значение функции). Обозначается она так: 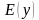 .
.
Нахождение области значений функции задача не из простых. Её можно находить алгебраическим способом, а можно графическим. Пока мы будем использовать графический способ. Для этого необходимо построить график заданной функции и по графику определить, какие значения может принимать зависимая переменная.
Графиком функции называется множество точек на координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции. (Напомним, что абсцисса – это координата х, ордината – координата у).
Поскольку, по определению функции, каждому значению аргумента соответствует только одно значение функции, то для графика соблюдается такое же правило: каждой абсциссе графика соответствует только одно значение ординаты.
Н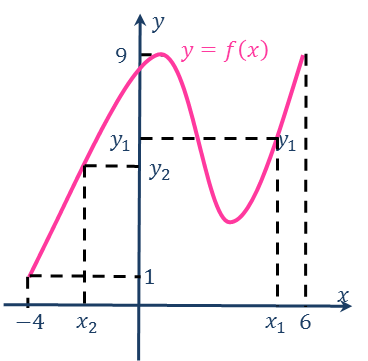 апример,
апример,
На графике показано, что абсциссе 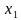 соответствует только одно значение
соответствует только одно значение 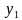 ; абсциссе
; абсциссе 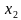 – только одно значение
– только одно значение 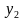 . И так далее.
. И так далее.
По графику выясняем, что его областью определения является множество всех действительных чисел, которые больше, либо равны, чем  , но меньше, либо равны, чем
, но меньше, либо равны, чем  т.е.
т.е. 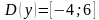 . А областью значений является множество всех чисел, которые больше, либо равны
. А областью значений является множество всех чисел, которые больше, либо равны 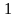 , но меньше, либо равны
, но меньше, либо равны  , т.е.
, т.е. 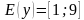 .
.
Вспомним функции, которые мы изучали в 7 и 8 классе.
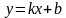 - линейная функция, графиком её является прямая, проходящая через точки
- линейная функция, графиком её является прямая, проходящая через точки  . Частными случаями линейной функции являются постоянная функция -
. Частными случаями линейной функции являются постоянная функция -  и прямая пропорциональность -
и прямая пропорциональность -  .
.
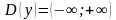

 – обратная пропорциональность, графиком её является гипербола, расположенная в I и III четверти, если
– обратная пропорциональность, графиком её является гипербола, расположенная в I и III четверти, если  , и во II и IV четверти, если
, и во II и IV четверти, если  .
.
 – квадратная функция, графиком её является парабола с вершиной в точке
– квадратная функция, графиком её является парабола с вершиной в точке  , ветви её направлены вверх и проходящая через точки
, ветви её направлены вверх и проходящая через точки  .
.
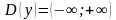
 – кубическая функция, графиком её является кубическая парабола с вершиной в точке
– кубическая функция, графиком её является кубическая парабола с вершиной в точке  , расположенная в I и III четверти.
, расположенная в I и III четверти.
 – функция квадратного корня, графиком её является ветвь параболы с вершиной в точке
– функция квадратного корня, графиком её является ветвь параболы с вершиной в точке  , расположенная в I четверти.
, расположенная в I четверти.

Функция задана формулой  . Найдите:
. Найдите:
Функция задана формулой  . Сравните числа:
. Сравните числа:
Решите уравнение  , если:
, если:
Решите неравенство  , если:
, если:
При каком значении параметра  график функции
график функции  :
:
проходит через точку 
проходит ниже точки 
проходи выше точки 
не проходит через точку  ?
?
Автомобиль движется по шоссе со скоростью 50 км/ч от пункта  до пункта
до пункта  , расстояние между которыми 200 км. Задайте функцию
, расстояние между которыми 200 км. Задайте функцию  (км) для
(км) для  (ч):
(ч):
расстояния от автомобиля до пункта 
расстояния от автомобиля до пункта 
расстояния от автомобиля до пункта  , находящегося на одинаковом расстоянии от пунктов
, находящегося на одинаковом расстоянии от пунктов  и
и  .
.
Без построения графика функции  найдите все точки этого графика:
найдите все точки этого графика:
с абсциссой  ;
;
с ординатой 
с равными координатами;
сумма координат которых равна нулю.
При каких значениях параметра  на графике функции
на графике функции  :
:
ровно одна точка с ординатой 
ровно две точки с ординатой 
нет точек с ординатой  ?
?
Дана функция . Во втором столбце таблицы укажите знак значения функции в точке 
Сопоставьте заданные функции с их областью определения:
| Функция | 
| 
| 3) | 
|
| Область определения |
|
|
|
|
Какие из данных функций определены на всём множестве действительных чисел:
Из данных высказываний выберите верные:
функция  определена для всех
определена для всех  из промежутка
из промежутка  ;
;
областью определения функции  является множество
является множество  ;
;
функция  определена для всех
определена для всех  из промежутка
из промежутка  ;
;
областью определения функции  является множество
является множество  .
.
Найдите область определения функций:
Для функции  найдите область определения и нули функции (те значения переменной, при которых значение функции равно нулю).
найдите область определения и нули функции (те значения переменной, при которых значение функции равно нулю).
Постройте графики функций:
Сопоставьте заданные функции с их областью значений:
| Функция | 
| 
| 3) | 
| 
|
| Область значений |
|
|
|
|
|
Для каждой из данных функций найдите её область значений:
Для каждой пары функций, приведённой в таблице, установите, совпадают их области определения или не совпадают.
| Функция | 
| 
| 
| 
| 
| 
|
| Функция | 
| 
| 
| 
| 
| 
|
| Да или нет |
|
|
|
|
|
|
Найдите область значений функции:
 при
при 
 при
при 
Представьте себе график функции  и, используя свой воображаемый график, найдите область значений этой функции, если:
и, используя свой воображаемый график, найдите область значений этой функции, если:
Найдите множество значений функции  при
при 
Укажите, какие из данных высказываний являются верными:
все значения независимой переменной образуют область значений функции;
корнем квадратным из неотрицательного числа  называется любое число
называется любое число  , такое, что
, такое, что  ;
;
уравнение  , если
, если  ;
;
квадратное уравнение имеет ровно один корень, если его дискриминант равен нулю;
областью определения функции  является множество всех чисел;
является множество всех чисел;
областью значений функции  является множество всех чисел;
является множество всех чисел;
если две стороны треугольника имеют длины 3 и 5, то областью значений длины третьей стороны этого треугольника является множество  .
.
Сколько различных целых значений принимает функция:
 при
при 
Постройте график функции
и определите:
область значений функции;
все такие значения  , для которых значение функции равно
, для которых значение функции равно  ;
;
все такие значения  , для которых значение функции равно
, для которых значение функции равно 
все такие значения функции, которые она принимает более одного раза.
При каких значениях параметра  уравнение
уравнение  имеет хотя бы один корень на множестве
имеет хотя бы один корень на множестве  . Найдите область значений функции
. Найдите область значений функции  при
при  .
.
5







 называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции).
называется такая зависимость переменной у от переменной х, что каждому значению переменной х соответствует только одно значение переменной у. Переменная х называется независимой (или аргументом), а переменная у – зависимой (или значением функции). .
.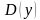 .
. 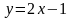 . Нам нужно определить, какие значения может принимать х. Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, областью определения функции является любое число, т.е.
. Нам нужно определить, какие значения может принимать х. Так как на 2 мы можем умножить любое число и от любого результата можем отнять 1, то х может принимать абсолютно любые значения. Значит, областью определения функции является любое число, т.е. 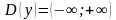 .
. 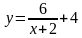 . Здесь мы замечаем, что х находится в знаменателе, а всем известно, что на 0 делить нельзя. Поэтому, мы находим число, при котором знаменатель станет равным 0. Это число
. Здесь мы замечаем, что х находится в знаменателе, а всем известно, что на 0 делить нельзя. Поэтому, мы находим число, при котором знаменатель станет равным 0. Это число 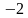 . Значит, х может принимать любые значения, кроме
. Значит, х может принимать любые значения, кроме 
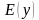 .
.  апример,
апример, 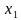 соответствует только одно значение
соответствует только одно значение 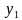 ; абсциссе
; абсциссе 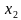 – только одно значение
– только одно значение 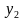 . И так далее.
. И так далее.  , но меньше, либо равны, чем
, но меньше, либо равны, чем  т.е.
т.е. 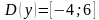 . А областью значений является множество всех чисел, которые больше, либо равны
. А областью значений является множество всех чисел, которые больше, либо равны 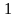 , но меньше, либо равны
, но меньше, либо равны  , т.е.
, т.е. 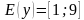 .
.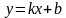 - линейная функция, графиком её является прямая, проходящая через точки
- линейная функция, графиком её является прямая, проходящая через точки  . Сравните числа:
. Сравните числа:









