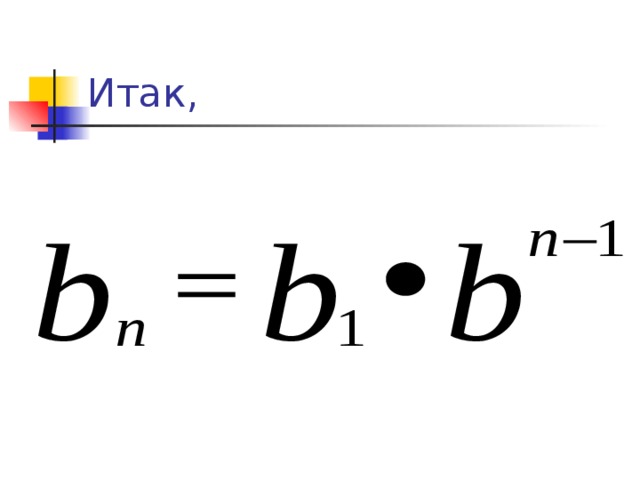Геометрическая прогрессия (алгебра, 9 класс)

Определение геометрической прогрессии. Формула n -го члена геометрической прогрессии

ЦЕЛЬ УРОКА :

• Формирование понятия геометрической прогрессии, используя сопоставление и противопоставления понятию арифметической прогрессии.
• Познакомить со свойствами геометрической прогрессии и формулой n- го члена.
• Закрепить на примерах решения задач.

Содержание урока:

• Самостоятельная работа с проверкой в классе.
• Организация изучения понятия геометрической прогрессии и введение формулы n- го члена геометрической прогрессии.
• Первичное применение знаний и умений.
• Подведение итогов работы на уроке.

Самостоятельная работа

В заданиях 1-3 дана арифметическая прогрессия. Найдите: 1 вариант 2 вариант

• двадцать третий член, если первый член -9 и разность 4.
• сумму десяти первых членов, если а = 4 n +2 , n – натуральное число.
• сумму семи первых членов прогрессии

-5;-3;-1;…

4. Продолжите числовую последовательность, записав еще 2 члена: -2;6;-18;…

• тридцать второй член, если первый член 65 и разность -2.
• сумму десяти первых членов, если а = 3n-1, n – натуральное число.
• сумму семи первых членов прогрессии 8;4;0;…
• Продолжите числовую последовательность, записав еще 2 члена: 1;2;4;…

Ответы к самостоятельной работе:

• 1 ВАРИАНТ

• 2 ВАРИАНТ

• 3
• 155
• -28
• 16; 32

• 79
• 240
• 7
• 54;-162

Изучение понятия геометрической прогрессии и вывод формулы n -го члена геометрической прогрессии.

4 задание 1 вариант 2 вариант

• 1; 2; 4; 8; 16;

1

1 2

2 2

4 2

8 2

• -2; 6; -18; 54; -162;

-2

-2 ( -3)

6 ( -3)

-18 ( -3)

54 ( -3)

Геометрической прогрессией называется последовательность отличных от нуля чисел, каждый член которой, начиная со второго, равен предыдущему члену, умноженному на одно и тоже число.

Определение

Числовая последовательность отличных от нуля чисел, в которой каждый следующий член получается из предыдущего умножением на одно и тоже число q , называется геометрической прогрессией .

Числовая последовательность, в которой каждый следующий член получается из предыдущего прибавлением одного и того же числом d ,называется арифметической прогрессией .

Число d – называется разностью арифметической прогрессии.

Число q – называется знаменателем геометрической прогрессии.

Обозначение

Арифметическая прогрессия

Геометрическая прогрессия

Допустимые значения

Геометрическая прогрессия

числа неравные нулю

Арифметическая прогрессия

любые числа

Рекуррентная формула

Арифметическая

прогрессия

Геометрическая

прогрессия

Нахождение

разность арифметической

прогрессии

знаменатель геометрической прогрессии

Используя рекуррентную формулу, получим формулу общего члена геометрической прогрессии.

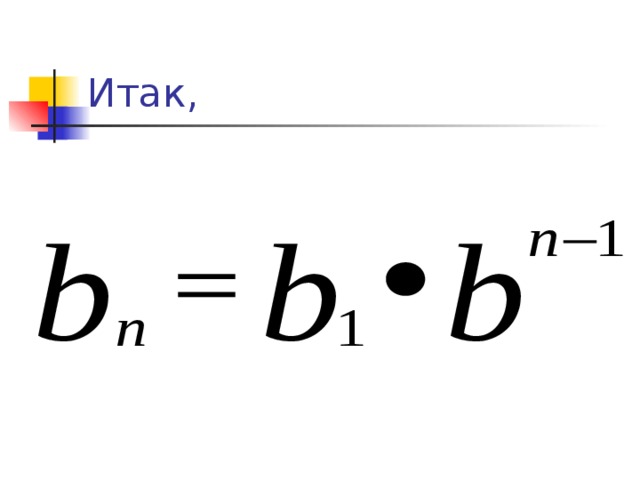
Итак,

Формула n- го члена

геометрическая

прогрессия

арифметическая

прогрессия

Характеристическое свойство

арифметическая

прогрессия

геометрическая

прогрессия

или

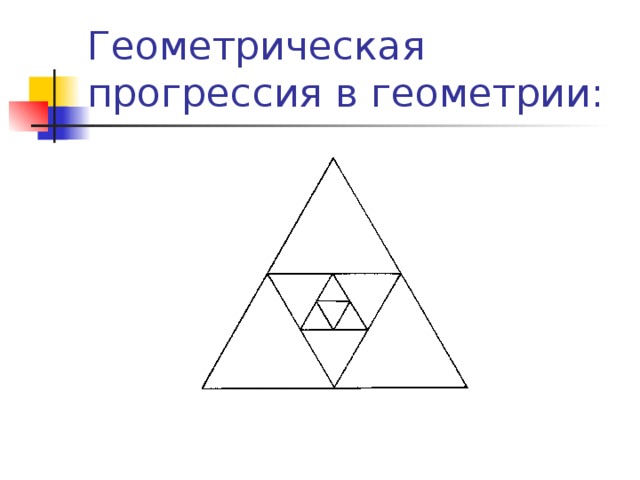
Геометрическая прогрессия в геометрии:

Решение задач

Задача 1

Найдите первые 5 членов

геометрической прогрессии , если

первый член -2, а знаменатель -0.5.

Ответ: -2; 1; -0,5; 0,25; - 0,125

Задача 2.

В правильный треугольник, сторона которого равна 16 см, вписан второй треугольник так, что его вершинами являются середины сторон первого. Во второй треугольник таким же способом вписан третий и т.д. Найдите периметр пятого треугольника.

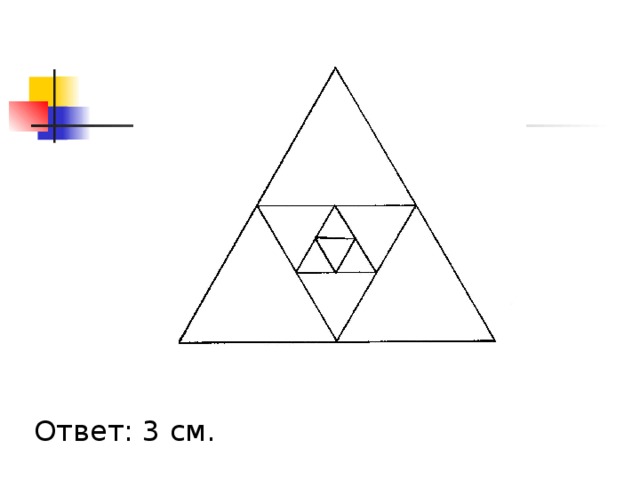
Ответ: 3 см.

Задача 3 (решить двумя способами)

Найдите знаменатель геометрической

прогрессии, если ее четвертый член

25, а шестой член 16.

Ответ:

Задача 4.

Между числами и 27 вставьте

четыре числа, чтобы получилась

геометрическая прогрессия.

Найдите эти числа.

Ответ: ; 1; 3; 9

Задача 5.

Дана геометрическая прогрессия ( ),

в которой и

Найти первый член геометрической

прогрессии.

Ответ: 12 или

Итог урока

Домашнее задание

• Придумать задачу, где используется геометрическая прогрессия.