Геометрические парадоксы

Слово «парадокс» происходит от греческого слова παράδοξος , которое означает "необычное, странное, невероятное, замечательное".

«Толковый словарь русского языка» под редакцией Д.И. Ушакова утверждает, что парадокс – это мнение, резко расходящееся с обычным, общепринятым, противоречащее здравому смыслу. 

Парадоксы в нашей жизни не так уж и редки. Они встречаются в логике (логические парадоксы – это рассуждения, приводящие к взаимно исключающим заключениям), в искусстве (парадокс используется авторами для поддержания интереса читателей, зрителей, слушателей), в науке (во многих областях науки логика используется как инструмент познания, что может привести к противоречию теории с результатом опыта).

Особое место занимают парадоксы в геометрии. В геометрии очень важны строгость и логическая последовательность доказательств. При этом часто возникают ситуации, в которых рассуждения, которые считались строгими при изучении одного материала, при изучении другого материала будут требовать дополнительного обоснования. Тогда математик просто излагает свои идеи в том виде, как они у него возникают. Однако часто возникает необходимость сделать выбор между некорректными, но плодотворными методами изложения, и корректными, но позволяющими выразить мысль лишь в измененном виде. Первый путь ведет к возникновению и развитию новых теорий, а, следовательно, и парадоксов, второй – к "затуханию науки".

Актуальность проекта: В настоящее время уроки геометрии, на мой взгляд, не всегда вызывают особый интерес у учащихся. Применение парадоксов может способствовать  повышению интереса к математике.

Цель работы: рассмотреть многообразие парадоксов в геометрии, выявить роль парадоксов в научном познании мира.

Задачи:

• определить понятие парадокса

• рассмотреть примеры парадоксов

• изучить решения и объяснения парадоксов

• определить значение парадокса для развития научного знания

Гипотеза: могут ли существовать геометрические парадоксы в реальном мире.

Объект исследования: геометрические парадоксы.

Предмет исследования: геометрия.

Методы исследования: анализ литературы по теме.

1. Парадоксы в математике

Математику называют царицей наук и считают самой точной и строгой областью научного исследования. Математический мир отличается идеальностью, логичностью и непротиворечивостью. Поэтому наличие парадоксов в математике – это факт сам по себе парадоксальный. 

За всю историю своего развития математика не раз испытывала потрясения, которые сопровождались обнаружением парадоксов. Их преодоление достигалось введением новых понятий, рассмотрением необычных идей. То есть парадоксы разрешались благодаря тому, что они порождали новые теории.

Одно из таких потрясений произошло в античные времена. Античные математики считали, что однородные величины (выражающие длины или площади) соизмеримы, то есть для них существует общая мера, которая целое число раз укладывается в данных однородных величинах. Но оказалось, что сторона квадрата и диагональ квадрата несоизмеримы. Парадокс состоял в том, что по отдельности и диагональ и сторона квадрата могут быть измерены и количественно точно определены. Однако выразить их длины через отношения друг к другу с помощью имевшихся тогда чисел не удавалось. Этот парадокс удалось преодолеть путём введения в математику √ (квадратного корня).

Еще один кризис в математике возник в XVII-XVIII веках и был связан с бесконечно малыми величинами.  Бесконечно малые – это переменные величины, стремящиеся к нулю. Парадокс возник потому что в одних случаях бесконечно малая величина приравнивалась к нулю и при вычислениях отбрасывалось, в других же – принималась как значение, отличное от нуля, о чем говорит и само название. Выход из кризиса был найден созданием теории пределов.

Наличие парадокса стимулирует к новым исследованиям, более глубокому осмыслению теории, её «очевидных» постулатов и нередко приводит к полному её пересмотру.

Таким образом, можно считать, что парадоксы возникают в науке там, где теория не описывает процессы должным образом. Разрешение таких парадоксальных явлений ведет в свою очередь к возникновению новых теорий.

.

1. Свойство парадоксов

Все парадоксы имеют одно общее свойство - самоприменимость (циркулярность). В каждом из них объект, о котором идет речь, характеризуется с помощью совокупности объектов, к которой он сам принадлежит. Если мы выделяем, например, самого хитрого человека, мы делаем это при помощи совокупности людей, к которой относится и данный человек. И если говорим: "Это высказывание ложно", мы характеризуем интересующее нас высказывание, ссылаясь на включающую его совокупность всех ложных высказываний.

Во всех парадоксах имеет место движение по кругу, приводящее, в конце концов, к исходному пункту. Стремясь охарактеризовать интересующий нас объект, мы обращаемся к той совокупности объектов, которая включает его. Однако оказывается, что сама эта совокупность для своей определенности нуждается в рассматриваемом объекте и не может быть ясным образом понята без него. В этом круге, возможно, и кроется источник парадоксов.

1. Устранение и решение парадоксов.

Устранение парадоксов и их разрешение - это не одно и то же.

Устранить парадокс из некоторой теории - значит перестроить ее так, чтобы парадоксальное утверждение оказалось в ней недоказуемым.

Каждый парадокс опирается на большое число определений, допущений и аргументов. Вывод парадоксального суждения представляет собой некоторую цепочку рассуждений. Можно подвергнуть сомнению любое звено этой цепочки, отбросить его и тем самым разорвать цепочку и устранить парадокс. Во многих работах так и поступают и этим ограничиваются. Но это еще не разрешение парадокса. Мало найти способ, как его исключить, надо убедительно обосновать предлагаемое решение. Само сомнение в каком-то шаге, ведущем к парадоксу, должно быть хорошо обосновано.

Прежде всего, решение об отказе от каких-то логических средств, используемых при выводе парадоксального утверждения, должно быть увязано с нашими общими соображениями относительно природы логического доказательства и другими логическими интуициями. Если этого нет, устранение парадокса оказывается лишенным твердых и устойчивых оснований и вырождается в техническую по преимуществу задачу.

Кроме того, отказ от какого-то допущения, даже если он и обеспечивает устранение некоторого конкретного парадокса, вовсе не гарантирует автоматически устранения всех парадоксов. Это говорит о том, что за парадоксами не следует "охотиться" поодиночке. Исключение одного из них всегда должно быть настолько обосновано, чтобы появилась определенная гарантия, что этим же шагом будут устранены и другие парадоксы.

Однако надо иметь в виду, что непродуманный и неосторожный отказ от слишком многих или слишком сильных допущений может привести просто к тому, что получится хотя и не содержащая парадоксов, но существенно более слабая теория, имеющая только частный интерес.

1. Примеры парадоксов в геометрии
   1. Невозможные фигуры Пенроуза

Треугольник Пенроуза (см. рис. 2.1) — одна из основных невозможных фигур, известная также под названиями невозможный треугольник и трибар. Был открыт в 1934 году шведским художником Оскаром Рутерсвардом, который изобразил его в виде набора кубиков. Широкую известность эта фигура обрела после опубликования статьи о невозможных фигурах в Британском журнале психологии английским математиком Роджером Пенроузом в 1958 году. Также в этой статье невозможный треугольник был изображен в наиболее общей форме — в виде трёх балок, соединённых друг с другом под прямыми углами.

Лестница Пенроуза (см. рис. 2.2) — это одна из основных невозможных фигур, открытая Оскаром Рутерсвардом. Модель её была разработана Лайонелом и Роджером Пенроузами. Представляет собой такую конструкцию лестницы, при которой в случае движения по ней в одном направлении человек будет бесконечно подниматься, а при движении в обратном — постоянно спускаться. При этом после завершения визуального маршрута человек окажется в той же точке, с которой начал своё передвижение. Лестница сконструирована таким образом, что существование её в реальном мире невозможно.

Эти фигуры — ничто иное как оптические иллюзии. Человеческий мозг адаптирует полученную информацию, когда видит такие изображения. Он не замечает противоречия в соединении элементов конструкции, а формирует ошибочную целостную картинку. Неправильное восприятие порождает оптическую иллюзию.

Р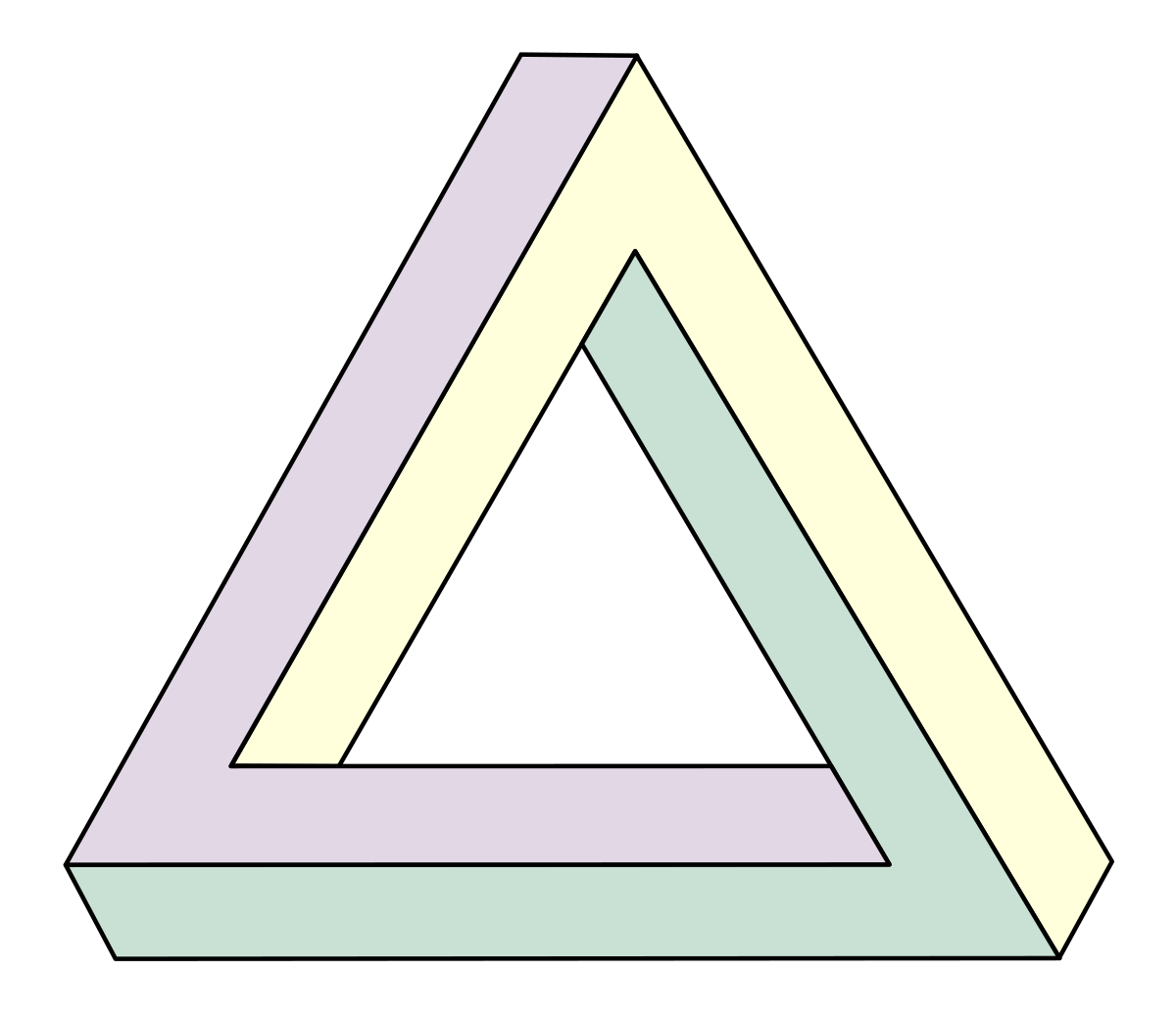
исунок 2.1 — Треугольник Пенроуза

Р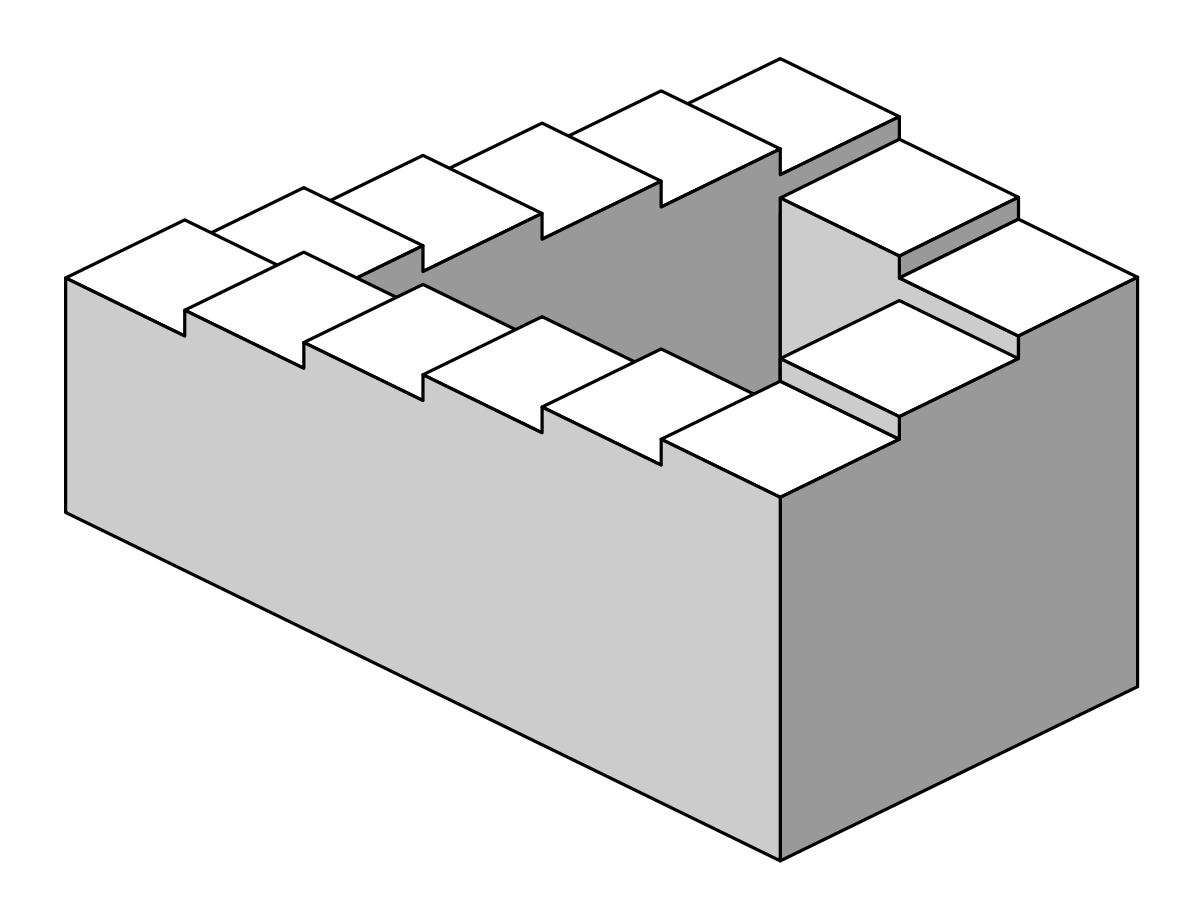
исунок 2.2 — Лестница Пенроуза

1. Парадокс Маляра

Парадокс маляра — математический парадокс, утверждающий, что фигуру с бесконечной площадью поверхности можно окрасить конечным количеством краски .

Рассмотрим бесконечную ступенчатую пластинку (см. рис. 2.3), состоящую из прямоугольников: первый из них — квадрат со стороной 1 см, второй имеет размеры 0,5 × 2 см, а каждый следующий вдвое уже и вдвое длиннее предыдущего. Площадь каждого прямоугольника равна 1 см², а общая площадь пластинки бесконечна.

Р
исунок 2.3 — Бесконечная ступенчатая пластинка

Чтобы всю её покрасить, потребуется бесконечное (по объёму или массе) количество краски. Рассмотрим тело, получаемое при вращении пластинки вокруг её прямого бесконечного края. Сосуд состоит из цилиндров. Высота k-го цилиндра равна _{ }см, радиус — _{ }см, а значит, его объём равен_{ }см³. Таким образом, объёмы цилиндров образуют убывающую геометрическую прогрессию, их сумма конечна и равна 2π см³.

Заполним этот сосуд краской. Погрузим в него данную бесконечную пластинку и вытащим; она будет окрашена конечным количеством краски с двух сторон.

Разрешение парадокса: Утверждение «для того, чтобы покрасить фигуру бесконечной площади, необходимо бесконечное количество краски» исходит из того, что фигура покрывается слоем краски одинаковой толщины. Предлагаемый же способ окраски предполагает, что каждый следующий сегмент будет покрыт всё более тонким слоем, так что, бесконечная сумма объёмов краски, ушедших на каждый сегмент площадью в 1π см², будет сходиться к конечному значению. При этом нужно иметь в виду, что предложенное математическое решение не учитывает тот физический факт, что слой краски не может иметь толщину меньше размера одной молекулы краски. Так как построенный описанным способом сосуд будет книзу сужаться до бесконечно малых диаметров, то при «заливке» краски в такой сосуд эта краска просто не «затечёт» в те его области, диаметр которых меньше диаметра молекулы краски. И тем не менее, с точки зрения математической модели, не учитывающей физические аспекты устройства нашего мира, описанное решение является верным, несмотря на парадоксальность.

1. 64=65

Возьмём квадрат со стороной 8 см и разрежем его как показано на рис. 4, а затем сложим из полученных частей прямоугольник. Получившийся прямоугольник имеет размеры 5 на 13 (см. рис. 2.4). Теперь сравним площади полученных фигур. Так как эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны .

Р
исунок 2.4 — Разрез квадрата и получившийся прямоугольник

Давайте теперь сравним площади полученных фигур. Так как эти две фигуры составлены из одинаковых кусков, то и площади этих фигур должны быть равны. Давайте сравним их: S квадрата=8*8=64 см² S прямоугольника=5*13=65 см², то есть мы получаем, что 64=65. Этот "парадокс" кажется неразрешимым. Действительно, трудно представить, что "извне" возникла "лишняя" единица! Оказывается, что длины сторон четырех частей, составляющих фигуры (см. рис. 2.4), являются членами ряда Фибоначчи. Расположение частей, на которые был разрезан квадрат, в виде прямоугольника иллюстрирует одно из свойств ряда Фибоначчи, а именно следующее: при возведении в квадрат любого члена этого ряда получается произведение двух соседних членов ряда плюс или минус единица. В нашем примере сторона квадрата равна 8, а площадь равна 64. Восьмерка в ряду Фибоначчи расположена между 5 и 13. Так как числа 5 и 13 становятся длинами сторон прямоугольника, то площадь его должна быть равной 65, что дает прирост площади в одну единицу.

Благодаря этому свойству ряда можно построить квадрат, стороной которого является любое число Фибоначчи, большее единицы, а затем разрезать его в соответствии с двумя числами, между которыми это число стоит.

Э
тот парадокс объясняется тем, что точки A, B, C, D (см. рис. 2.5) на самом деле не лежат на одной прямой, а являются вершинами параллелограмма, площадь которого как раз и равна "лишней" единице

Рисунок 2.5 — Точный рисунок полученного прямоугольника

1. Геометрические парадоксы в жизни

Как говорилось до этого, невозможные фигуры всего лишь являются иллюзиями в виде рисунков. Но могут ли они существовать в реальном мире? Для того, чтобы ответить на этот вопрос, я начал искать нужную информацию. В процессе поиска я нашёл скульптуры, посвященные такой невозможной фигуре, как треугольник Пенроуза. Оказывается, что в Австралии, в городе Перт, есть вот такая скульптура (см. рис. 3.1).

Р
исунок 3.1 — Треугольник Пенроуза в Австралии

Но, чтобы увидеть такую фигуру, на скульптуру нужно смотреть под определённым ракурсом. В других же ракурсах, скульптура приобретает совсем другой вид (см. рис. 3.2).

Р исунок 3.2 — Треугольник Пенроуза в трёх ракурсах

Возведение в реальность остальных невозможных фигур я не обнаружил. Что касаемо задач с геометрическими парадоксами, то их конечно не может быть в реальном мире.

Также меня заинтересовало, можно ли сделать такую фигуру своими руками при помощи материалов, которые есть у каждого дома. Я наткнулся на интересную статью о том, как это можно сделать.

Треугольник Пенроуза можно собрать самостоятельно. К примеру, из бумаги или картона. И помогут в этом схемы (см. рис. 3.3). Их нужно всего лишь распечатать и склеить.

Р
исунок 3.3 — Схема для Треугольника Пенроуза

Первым этапом для его создания является подготовка схемы. Она переносится на бумагу (картон) с помощью принтера. А далее все еще проще. Ее нужно просто вырезать по периметру. На схеме уже имеются все необходимые линии. Удобнее будет работать с более плотной бумагой. Если схема распечатана на тонкой бумаге, а хочется чего-то поплотнее, заготовка просто прикладывается на выбранный материал и вырезается по контуру. Чтобы схема не сдвигалась, ее можно прикрепить скрепками. Далее нужно определить те линии, по которым заготовка будет сгибаться. Как правило, на схеме она представлена пунктирной линией. Сгибаем деталь. Далее определяем места, которые подлежат склеиванию. Они промазываются клеем ПВА. Деталь соединяется в единую фигуру. Деталь можно раскрасить. А можно изначально использовать цветной картон. В своём случае, я сделал её из обычной бумаги и клея(см. Рис. 3.4). Чтобы разглядеть Треугольник Пенроуза, как и в случае со скульптурами, нужно посмотреть с определённого ракурса. С другого ракурса никакого треугольника видно не будет (см. рис. 3.5).

Р
исунок 3.4 — Оригами Треугольника Пенроуза

Р
исунок 3.5 — Оригами Треугольника Пенроуза с другой стороны

В заключении можно отметить, что парадоксы в науке имеют противоречивую природу. С одной стороны они обозначают кризис старого научного знания, с другой – они способствуют развитию нового, это доказывает их полезность и даже определенную необходимость.

Количество существующих парадоксов по-настоящему огромное. Они присутствуют везде – и в повседневной жизни, и в науке. Практически в каждой научной области исследования существуют свои парадоксы. Даже такие точные, строгие и непротиворечивые науки как логика и математика не смогли остаться «непарадоксальными».

В геометрии существуют парадоксы, которые так или иначе решаются.

Геометрические парадоксы не могут существовать в реальном мире в том виде, котором они изображены на рисунках.

Исследовать геометрические парадоксы действительно очень интересно и необычно. Благодаря парадоксам можно научиться искать ошибки в рассуждениях других, грамотно строить свои рассуждения и логические объяснения.

1. wikipedia.org [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Парадокс;

2. wikipedia.org [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Треугольник_Пенроуза ;

3. wikipedia.org [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Лестница_Пенроуза;

4. wikipedia.org [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Категория:Математические_парадоксы ;

5. gimn1567.ru [Электронный ресурс]. – Режим доступа: http://gimn1567.ru/dost/fibonach/geometr.htm;

6. А. Панов, Малярный парадокс // Квант. — 1986. — № 8. — С. 13.

7. https://works.doklad.ru/view/DFvJdM2noYc/6.html

8. https://gtmarket.ru/concepts/6956