Геометрия фракталов

Фракталы.

Перед вами предмет, который станет отправной точкой моего выступления, и я предлагаю вам отгадать, что это, если:

• Её Родина – Малая Азия и Восточное Средиземноморье.

• Она прекрасный источник витамина С, по содержанию этого витамина она в 2,5 раза превосходит цитрусовые.

• Она содержит минералы – бор, железо, йод, калий, кальций, натрий, магний, марганец, медь, хром; углеводы и белки.

• Название этого овоща происходит от итальянского слова "брокко", что означает побег или ветка.

– Итак, это капуста брокколи. А что же общего между капустой брокколи и математикой? Давайте рассмотрим её строение. Что в ней особенного? (Капуста режется на фрагменты, они сравниваются и данные анализируются. Замечают, что мелкие фрагменты капусты похожи на саму капусту). Верно, она состоит из частей, которые подобны самой капусте.

Так вот фигуры, состоящие из элементов, похожих на всю фигуру называют фракталами.

Просмотр видео.

Фрактал - это такой объект, рассматривая который в увеличительное стекло, при всех его увеличениях мы увидим одну и ту же структуру.

Само слово фрактал произошло от латинского fractus – разбитый (поделенный на части).

Этот термин был введен математиком Бенуа Мандельбротом в 1975 году и с тех пор активно развилось направление фрактальной геометрии, которая изучает фрактальные фигуры.

Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:

• обладают нетривиальной структурой на всех шкалах;

• содержат произвольно малые масштабы;

• обладают свойством самоподобия;

• обладают дробной "фрактальной" размерностью;

• могут быть построены при помощи рекурсивной процедуры;

• слишком нерегулярны, чтобы быть описанными на традиционном геометрическом языке.

А рассмотренное множество Мандельброта - это классический пример фрактала.

А где же в природе мы еще можем встретить фракталы?

На самом деле многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, морозные узоры на окнах, кровеносная системы человека и животных, человеческая психология… Природа зачастую создает удивительные и прекрасные фракталы, с идеальной геометрией

1. Это Романеску, или романская брокколи, цветная коралловая капуста.

2. Каждый из нас хотя бы раз в жизни держал в руках и рассматривал морскую раковину. Обычно раковины являются красивым сувениром, напоминающим о поездке на море. Когда смотришь на это спиралевидное образование беспозвоночных моллюсков, нет никаких сомнений в его фрактальной природе.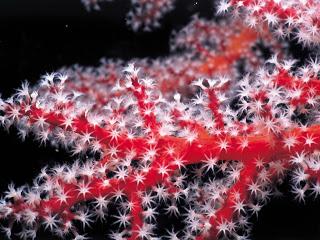

3. Еще одни типичнейшим представителем фрактального подводного мира является коралл. В природе известно свыше 3500 разновидностей кораллов, в палитре которых различают до 350 цветовых оттенков. Их огромные скопления образуют целые коралловые рифы.

Фрактал – это прежде всего язык геометрии.

Геометрические фракталы - самый первый, ранний тип фракталов, с которых, по сути, и началась история фракталов. Такие фракталы – одни из самых наглядных, в них сразу видна самоподобность частей, и получаются они путем простых геометрических построений:

1. Задается фигура (нулевое поколение), на основе которой будет строиться фрактал.

2. Задается процедура-генератор, которая на основе определенного правила (или правил) преобразует нулевое поколение.

3. Бесконечное повторение процедуры-генератора позволяет получить геометрический фрактал.

К геометрическим фракталам относятся: треугольник Серпинского, ковер Серпинского, кривая Коха, снежинка Коха, квадратная кривая Коха.

Рис. 1. Последовательные итерации построения треугольника Серпинского

Фрактал «треугольник Серпинского» был получен в 1915 г. польским математиком Вацлавом Серпинским. Для его получения используется равносторонний треугольник. На первом этапе построения необходимо разделить этот треугольник средними линиями на 4 треугольника, и изъять внутренний из них. После этого эти же действия повторить с каждым из оставшихся трех треугольников, и т.д. (см. рис. 1). Треугольник Серпинского имеет нулевую площадь.

Снежика Коха.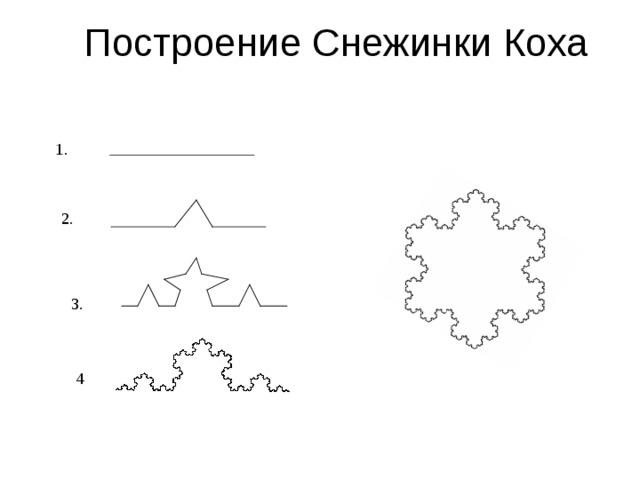

Вспомним знакомую из школьного курса геометрии теорему Пифагора. Пифагор, доказывая свою знаменитую теорему, построил фигуру, где на сторонах прямоугольного треугольника расположены квадраты («пифагоровы штаны»). Площадь квадрата, построенного на гипотенузе, равна сумме площадей квадратов, построенных на катетах. В наш век эта фигура Пифагора выросла в целое дерево. Впервые дерево Пифагора построил А. Е. Босман (1891—1961) во время Второй мировой войны, используя обычную чертёжную линейку. Если в классическом дереве Пифагора угол равен 45 градусам, то также можно построить и обобщённое дерево Пифагора при использовании других углов. Такое дерево часто называют «обдуваемое ветром дерево Пифагора».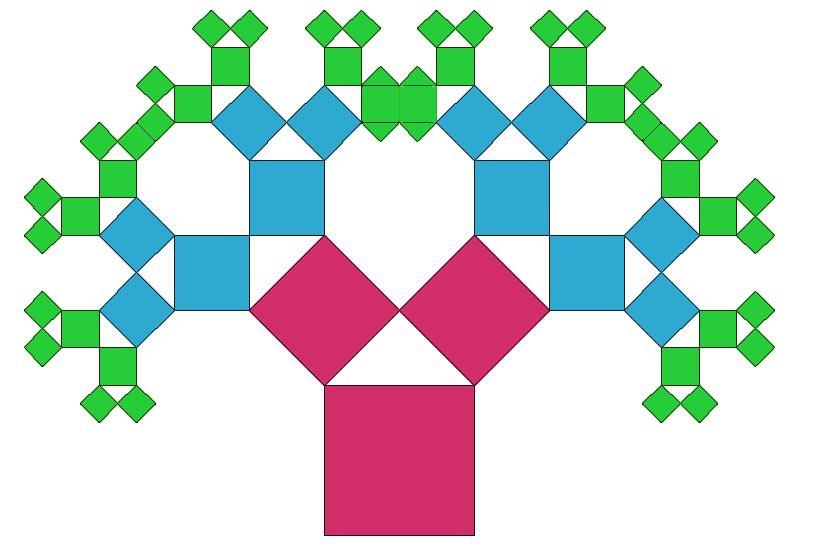

Алгебраические фракталы.

Эта группа фракталов строится на основе алгебраических формул, зачастую очень простых. Различают линейные и нелинейные алгебраические фракталы. Первые определяются линейными функциями (уравнениями первого порядка), а вторые – нелинейными (их природа значительно ярче, богаче и разнообразнее).

Применение фракталов.

Фракталам находят применение во многих сферах жизни: от искусства до фондовых рынков.

1. Рукоделие:

Квиллинг - повторение одних и тех же элементов в разных размерах – конечно же, это принцип фрактальности.

Вышивка - широко распространённый вид декоративно-прикладного искусства.

1. Дизайн -

1. Архитектура. Исторический музей в Москве – прекрасный тому пример. Башни пирамидальной формы, являясь самостоятельным элементом, создают общую зигзагообразную линию постройки и в то же время повторяются в мелких деталях, из которых и состоят.

В Японии за основу свадебной часовни взяли один из наиболее распространенных мотивов – спираль. Именно она является универсальным фракталом, так как в абсолютно любой части подобна самой себе.

Рынок.. Технический анализ для прогнозирования использует математические свойства изменения цен, а не экономические показатели ценных бумаг.

В середине двадцатого века известный американский финансист Ральф Эллиот предложил свою теорию поведения цен на акции, которая была основана на использовании теории фракталов. Эллиот исходил из того, что геометрия фракталов имеет место быть не только в живой природе, но и в общественных процессах. К общественным процессам он относил и торговлю акциями на бирже.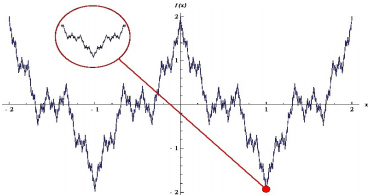

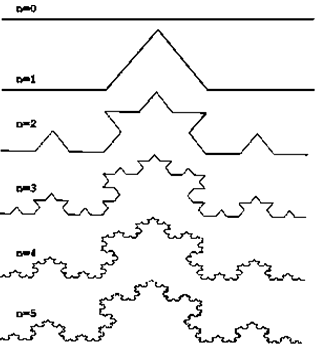
Телекоммуникации. Для передачи данных на расстояния используются антенны, имеющие фрактальные формы, что сильно уменьшает их размеры и вес. Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приемнику. Оказалось, что такая антенна работает не хуже обычной. Коэн основал собственную компанию и наладил их серийный выпуск. В данный момент американская фирма "Fractal Antenna System” разработала антенну нового типа, что позволило отказаться от использования в мобильных телефонах торчащих наружных антенн. Так называемая фрактальная антенна располагается прямо на основной плате внутри аппарата.

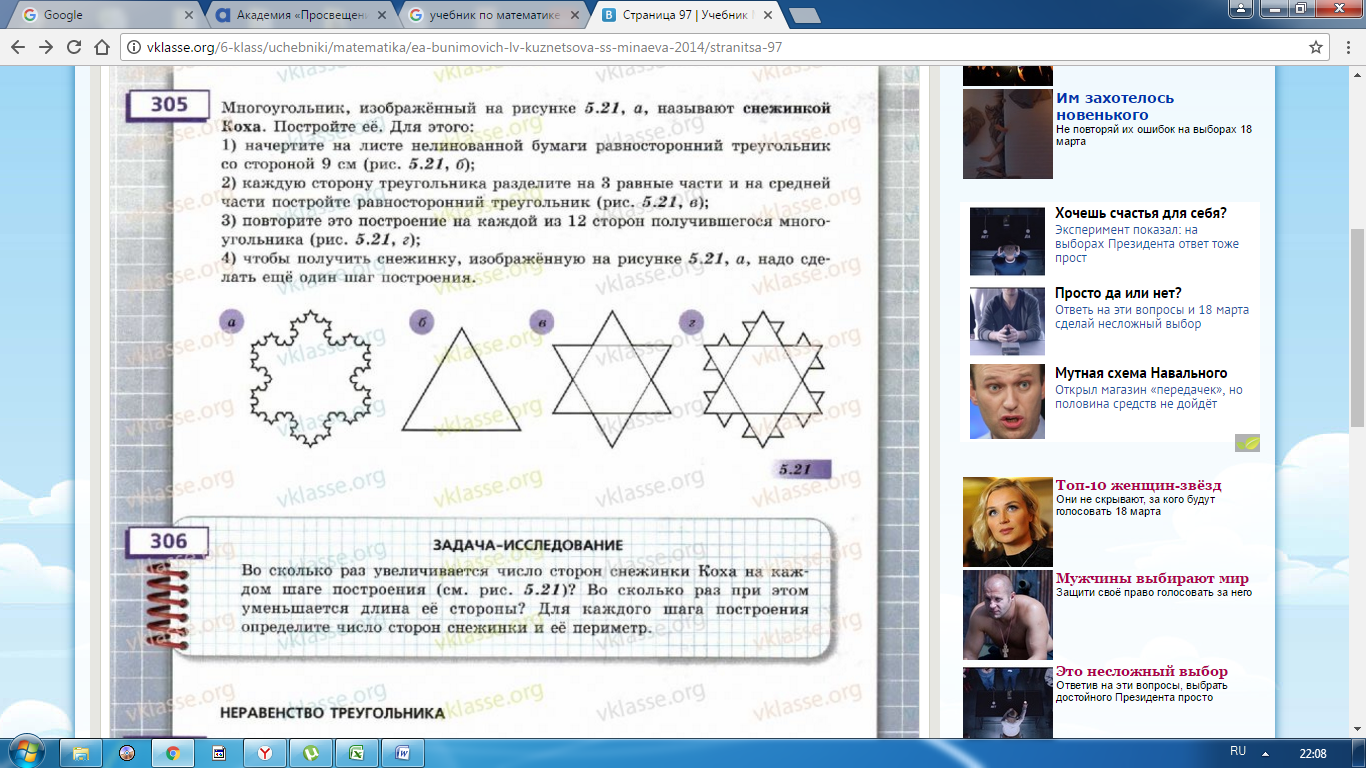
Такую антенну может смастерить любой школьник. В учебнике математики за 6 класс приводится пример построения снежинки Коха.

Литература. Среди литературных произведений находят такие, в тексте которых прослеживается фрактальная природа. В таких произведениях бесконечно повторяются элементы текста:

- неразветвляющееся бесконечное дерево, тождественное само себе с любой итерации (повторения) («У попа была собака…»

- неразветвляющиеся бесконечные тексты тексты с наращениями («Дом, который построил Джек»);

- «рассказы в рассказе» («Книга тысячи и одной ночи»,

Компьютерная графика. Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и т. д. Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, получить линии и поверхности очень сложной формы. Фрактальная компьютерная графика широко используется при создании мультфильмов и фантастических художественных фильмов.

Фракталы на кухне.

На праздничном столе мы можем встретить такие фракталы:

Как видно, фрактальность проявлена в нашем мире невероятно многогранно, имеет как практическую, так и эстетическую ценность, что само по себе, с точки зрения организации всего нашего мира, является примером фрактала.

И в завершении фрактальный новогодний лес.

Источники:

1. http://fractalsreality.blogspot.com

2. http://berlogos.com/article/fraktaly-v-arhitekture

3. https://novainfo.ru/article/3951

4. http://pochit.ru/informatika/31131/index.html

5. http://anysite.ru/publication/fractal