Геометрия в задачах ЕГЭ

Подготовка к ЕГЭ.

Задачи 13, 16 - базовый уровень.

8 - профильный уровень

1. Во сколько раз увеличится объем куба, если все его ребра увеличить в 5 раз?

2. Масса бетонного кубика равна 0,5 т. Сколько тонн будет масса куба, сделанного из того же бетона, но ребро которого в 2 раза больше, чем ребро маленького куба?

3. Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба

4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10

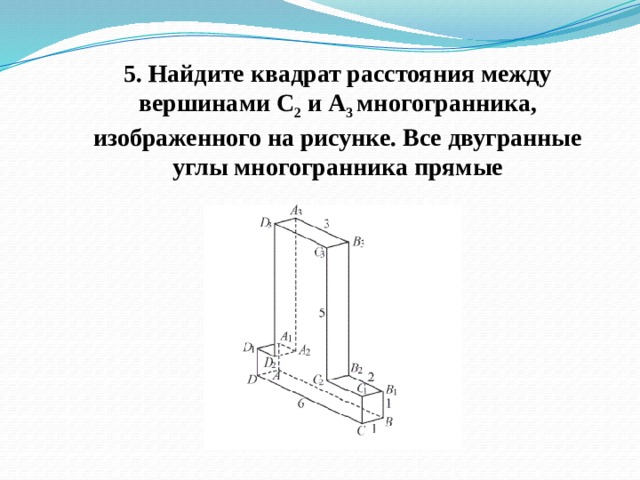
5. Найдите квадрат расстояния между вершинами С 2 и А 3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые

6. Во сколько раз увеличится площадь поверхности правильной пирамиды, если все ее ребра увеличить в 7 раз?

7. Пирамида Хефрена имеет форму правильной четырёхугольной пирамиды, сторона основания которой равна 210 м, а высота —  136 м. Сторона основания точной музейной копии этой пирамиды равна 105 см. Найдите высоту музейной копии. Ответ дайте в сантиметрах

8. Площадь боковой поверхности правильной треугольной пирамиды SABC равна 72, а площадь полной поверхности пирамиды SMNQ, отсекаемой от первой плоскостью, параллельной основанию и проходящей через середину высоты, равна 24. Найти площадь треугольника АВС

9. В бак, имеющий форму прямой призмы, налито 12 л воды. После полного погружения в воду детали уровень воды в баке увеличился в 1,5 раза. Найдите объём детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров

10. В бак цилиндрической формы, площадь основания которого 80 квадратных сантиметров, налита жидкость. Чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если после её погружения уровень жидкости в баке поднялся на 10 см. Ответ дайте в кубических сантиметрах

11. В цилиндрический бак налито 240 л воды, при этом уровень жидкости оказался равным 90 см. На сколько сантиметров поднимется уровень воды, если в этот бак полностью погрузить деталь объемом 800 см 3 ?

12. Даны две кружки цилиндрической формы. Первая кружка вдвое выше второй, а вторая в четыре раза шире первой. Во сколько раз объем второй кружки больше объема первой?

13.Радиус основания цилиндра равен 15, а его образующая равна 14. Сечение, параллельное оси цилиндра, удалено от неё на расстояние, равное 12. Найдите площадь этого сечения

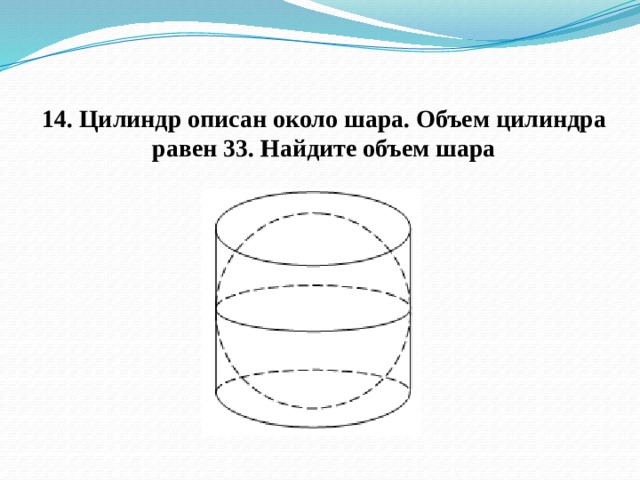
14. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара

15. Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 4. Объем параллелепипеда равен 16. Найдите высоту цилиндра

16. Чтобы приготовить торт цилиндрической формы, Марина использует 0,25 кг масла. Сколько масла (в кг) нужно взять Марине, чтобы сделать торт той же формы, но в два раза шире и в два раза выше?

17. Во сколько раз уменьшится объем конуса, если его высоту уменьшить в 5 раз?

18. Объём конуса равен 250. Через точку, делящую высоту конуса в отношении 1:4 , считая от вершины, проведена плоскость, параллельная основанию. Найдите объём конуса, отсекаемого от данного конуса проведённой плоскостью

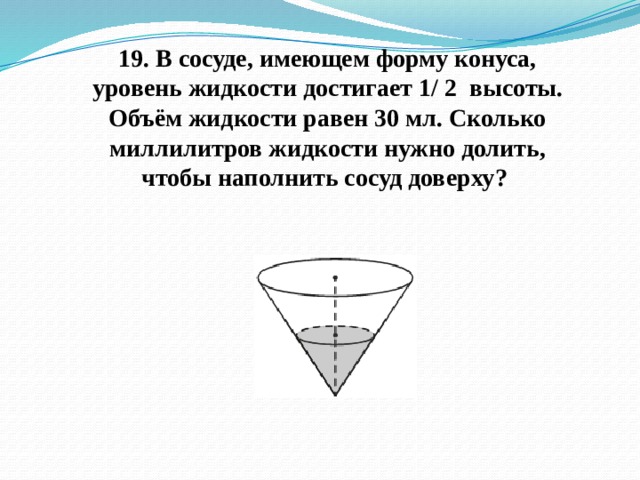
19. В сосуде, имеющем форму конуса, уровень жидкости достигает 1/ 2  высоты. Объём жидкости равен 30 мл. Сколько миллилитров жидкости нужно долить, чтобы наполнить сосуд доверху? 

  20. Однородный шар диаметром 6 см весит 216 грамм. Сколько грамм весит шар диаметром 7 см, изготовленный из того же материала?

Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды

S

S пов-ти. =S осн. + S бок.

S бок. = PL

Проведем апофему L

S осн. =

Найдем периметр основания

P=

L=

S бок. = = 240

S осн. = = 100

S пов-ти. = 100+240=340

13

D

C

K

A

10

B

S

Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды

V= S осн.* h

Проведем высоту и соединим ее с одним из углов основания. Получили прямоугольный треугольник SOD, где OD- радиус описанной окружности.

а 6 =R OD= 2

SO=

S осн. = а 2 √3

S осн. =

V= = 12

4

F

E

A

O

D

2

C

B

  Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна √3

V= S осн.* h

S треуг. =

V= =0,25

S треуг. = а 2 √3

√ 3

O

1

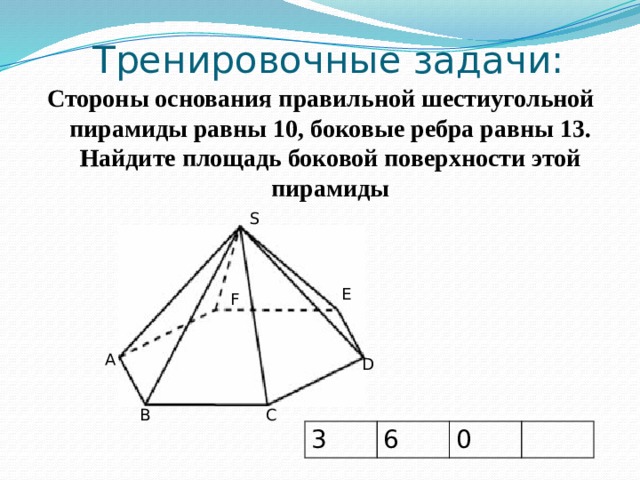
Тренировочные задачи:

Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды

S

E

F

A

D

B

C

3

6

0

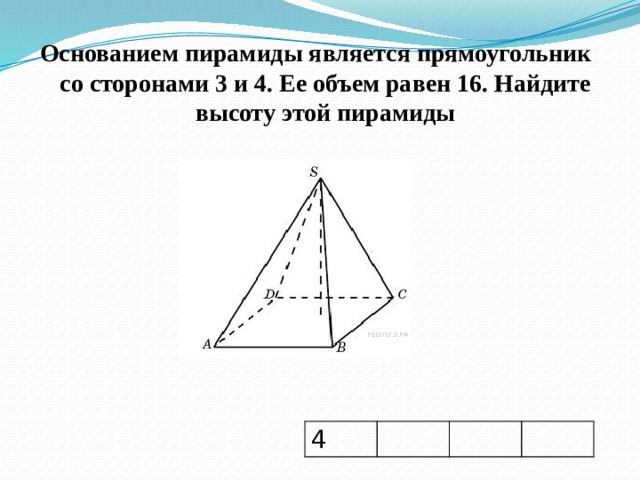
Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды

4

Формулы для решения задач с призмами

V куб = a 3 V=S осн h

S куб = 6a 2 S= 2ab+2bc+2ac

S бок. = n S гр.

S полн. = 2S осн. + S бок.

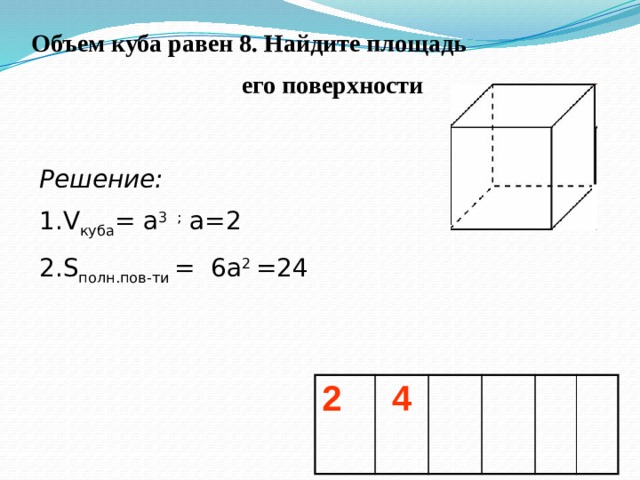
Объем куба равен 8. Найдите площадь

его поверхности

Решение:

• V куба = a 3 ; a=2
• S полн.пов-ти = 6a 2 =24

2

4

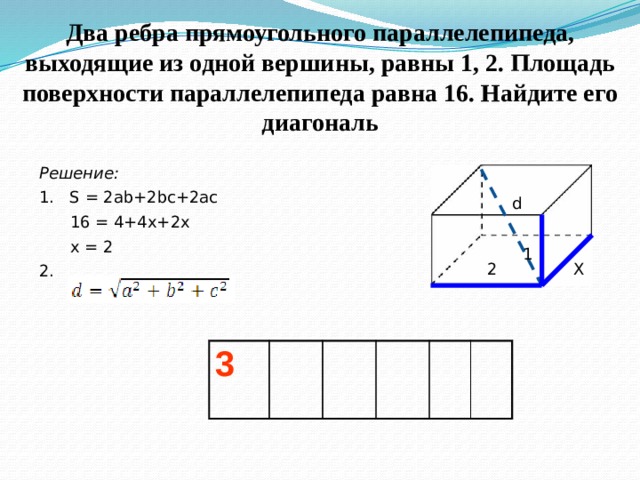
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ

Решение:

1. S = 2ab+2bc+2ac

16 = 4+4x+2x

x = 2

2.

d = 3

d

1

2

Х

3

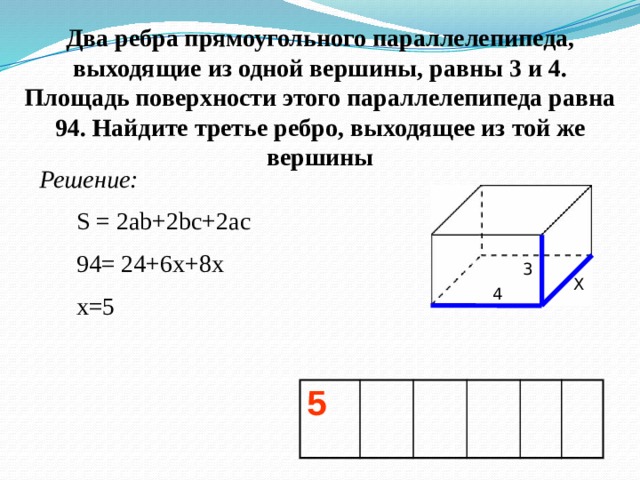
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины

Решение:

S = 2ab+2bc+2ac

94= 24+6x+8x

x=5

3

Х

4

5

.

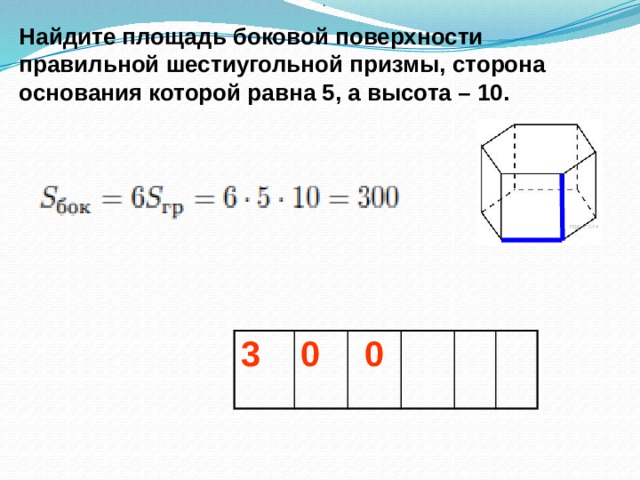
Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота – 10.

3

0

0

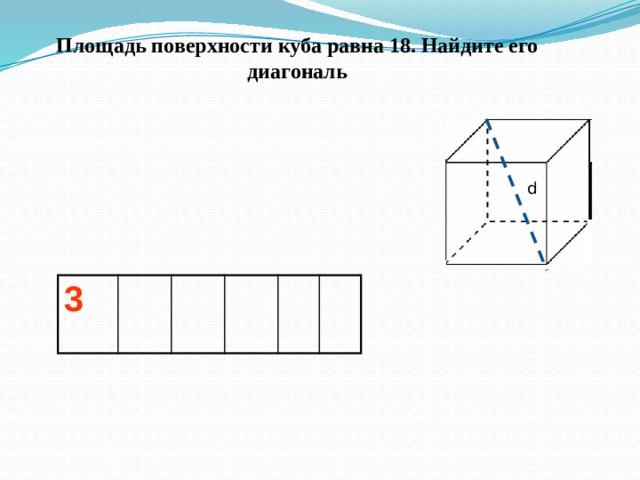
Площадь поверхности куба равна 18. Найдите его диагональ

d

3

Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 3, а высота — 7.

1

2

6

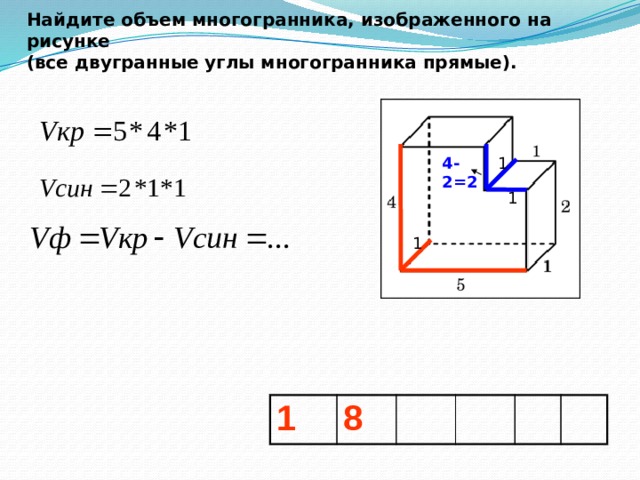
Найдите объем многогранника, изображенного на рисунке

(все двугранные углы многогранника прямые).

1

4-2=2

1

1

1

8

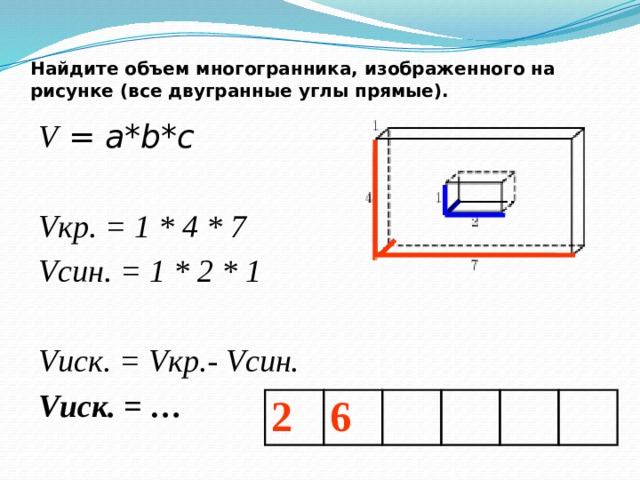
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

V = a*b*c

Vкр. = 1 * 4 * 7

Vсин. = 1 * 2 * 1

Vиск. = Vкр.- Vсин.

Vиск. = …

2

6

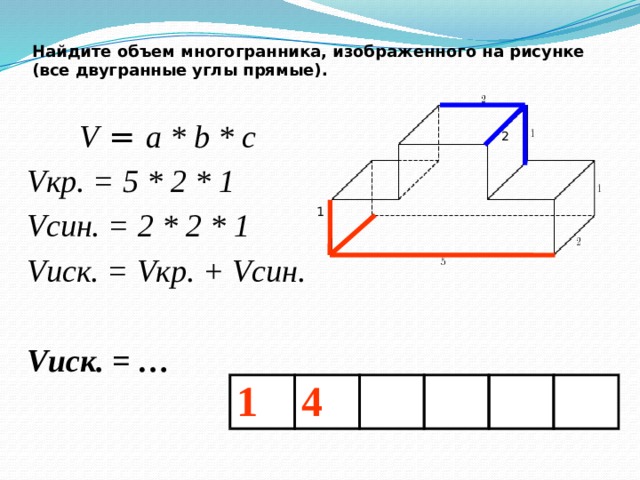
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

V = a * b * c

Vкр. = 5 * 2 * 1

Vсин. = 2 * 2 * 1

Vиск. = Vкр. + Vсин.

Vиск. = …

2

1

1

4

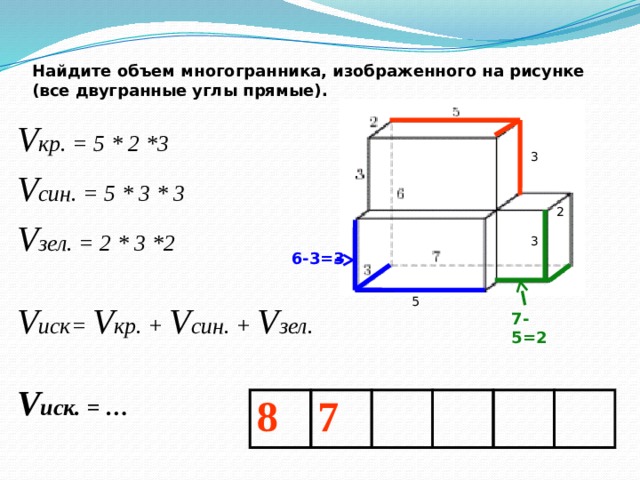
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

V кр. = 5 * 2 *3

V син. = 5 * 3 * 3

V зел. = 2 * 3 *2

V иск= V кр. + V син. + V зел.

V иск. = …

3

2

3

6-3=3

5

7-5=2

8

7

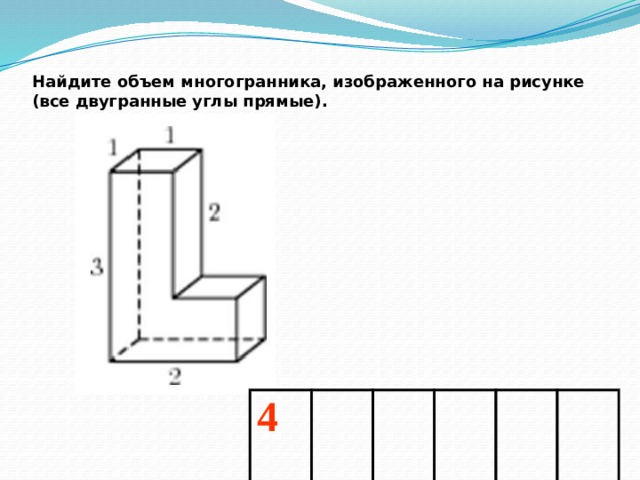
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

4

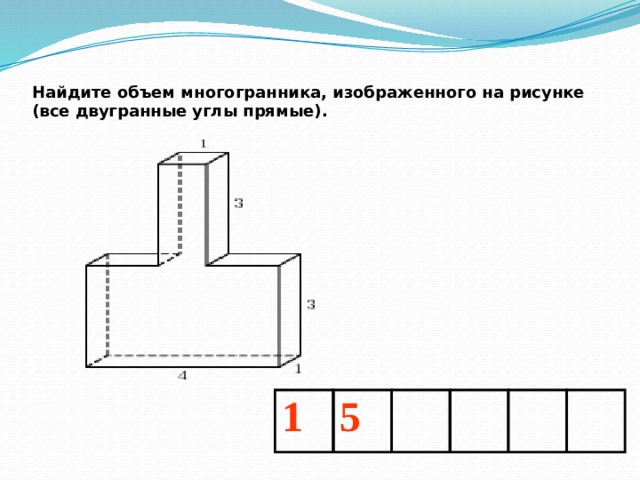
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

1

5

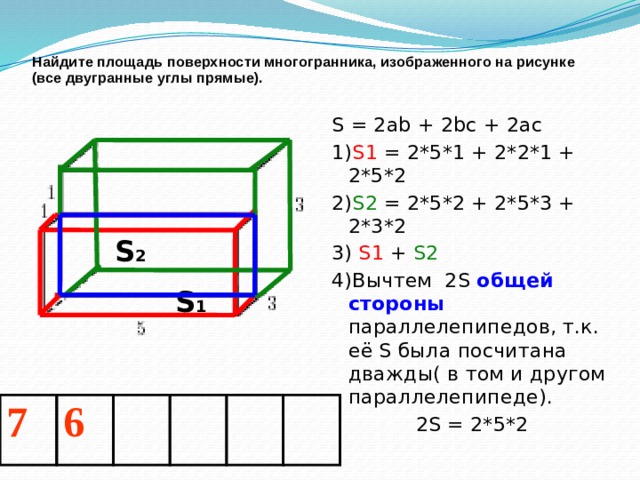
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

S = 2ab + 2bc + 2ac

1) S1 = 2*5*1 + 2*2*1 + 2*5*2

2) S2 = 2*5*2 + 2*5*3 + 2*3*2

3) S1 + S2

4)Вычтем 2S общей стороны параллелепипедов, т.к. её S была посчитана дважды( в том и другом параллелепипеде).

2S = 2*5*2

S 2

S 1

7

6

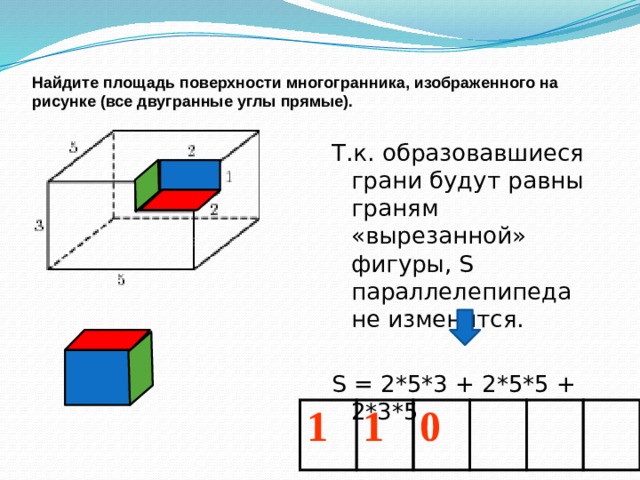
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Т.к. образовавшиеся грани будут равны граням «вырезанной» фигуры, S параллелепипеда не изменится.

S = 2*5*3 + 2*5*5 + 2*3*5

1

1

0

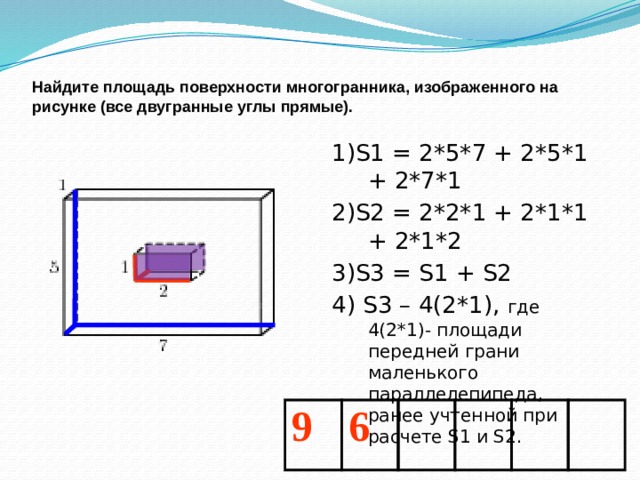
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

1)S1 = 2*5*7 + 2*5*1 + 2*7*1

2)S2 = 2*2*1 + 2*1*1 + 2*1*2

3)S3 = S1 + S2

4) S3 – 4(2*1), где 4(2*1)- площади передней грани маленького параллелепипеда, ранее учтенной при расчете S1 и S2.

9

6

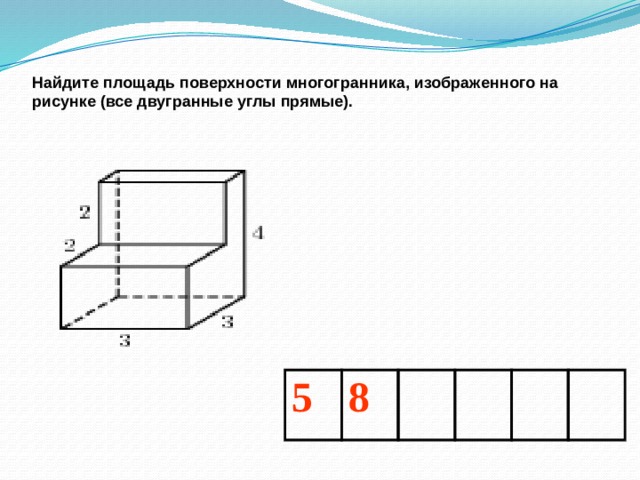
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

5

8

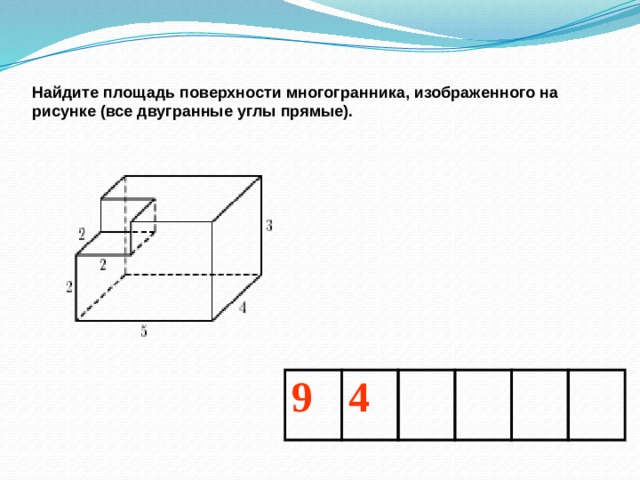
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

9

4

Фигура внутри фигуры

V призмы = Sh V пирамиды = 1/3 Sh S паралеллограмма = ah где а – сторона, h – высота, проведённая к ней

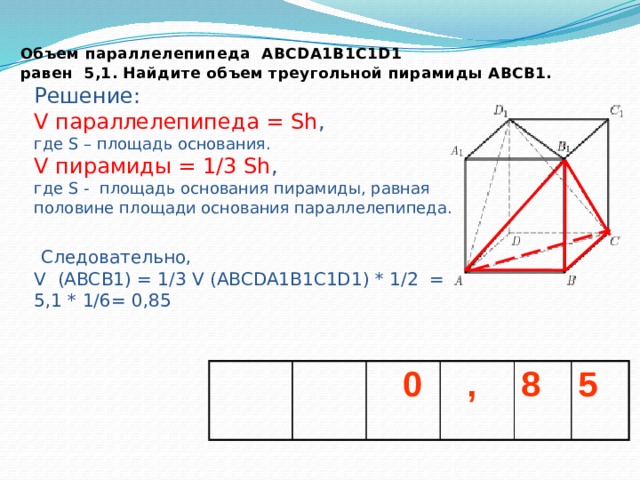
Объем параллелепипеда  ABCDA1B1C1D1 равен 5,1. Найдите объем треугольной пирамиды ABCB1.

Решение: V параллелепипеда = Sh , где S – площадь основания. V пирамиды = 1/3 Sh , где S - площадь основания пирамиды, равная половине площади основания параллелепипеда. Следовательно, V (ABCB1) = 1/3 V (ABCDA1B1C1D1) * 1/2 = 5,1 * 1/6= 0,85

0

,

8

5

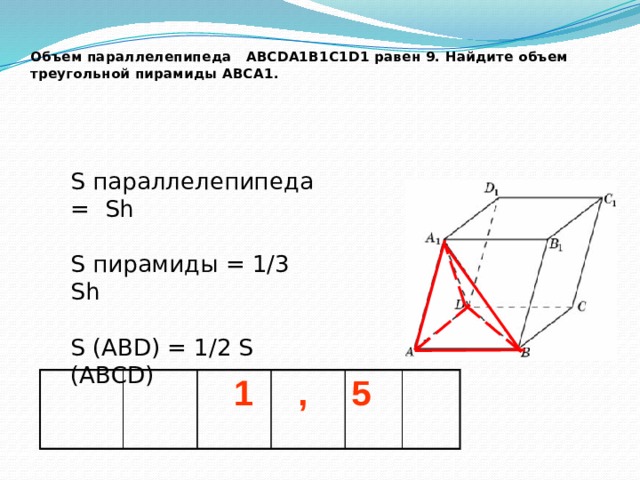
Объем параллелепипеда   ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1.

S параллелепипеда = Sh S пирамиды = 1/3 Sh S (ABD) = 1/2 S (ABCD)

1

,

5

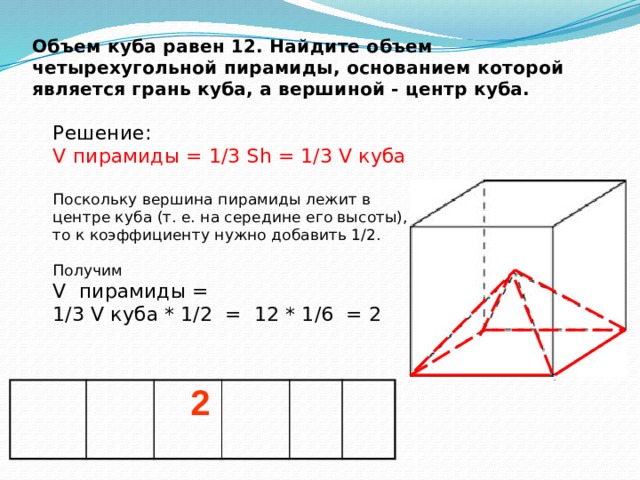
Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной - центр куба.

Решение: V пирамиды = 1/3 Sh = 1/3 V куба Поскольку вершина пирамиды лежит в центре куба (т. е. на середине его высоты), то к коэффициенту нужно добавить 1/2. Получим V пирамиды = 1/3 V куба * 1/2 = 12 * 1/6 = 2

2

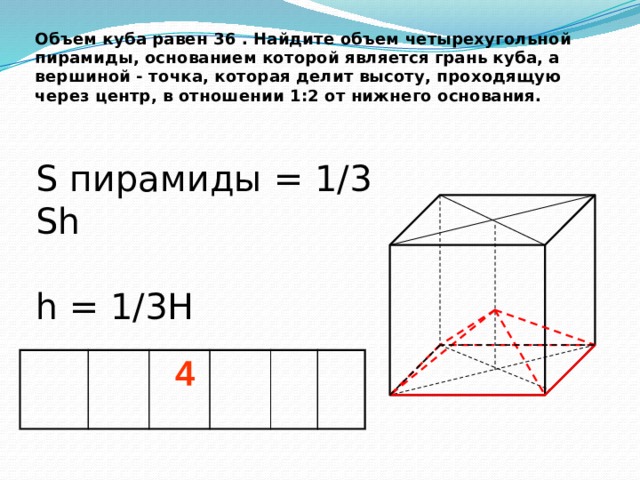
Объем куба равен 36 . Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной - точка, которая делит высоту, проходящую через центр, в отношении 1:2 от нижнего основания.

S пирамиды = 1/3 Sh h = 1/3H

4