ОГЭ. Решение задач по геометрии повышенного уровня сложности

Подготовка к ГИ А

Модуль «Геометрия» Решение задач повышенного и высокого уровня сложностей

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Задача 1 (повышенный уровень сложности)

Катеты прямоугольного треугольника равны 15 и 20. Найдите высоту, проведенную к гипотенузе

А

Н

15

?

В

С

20

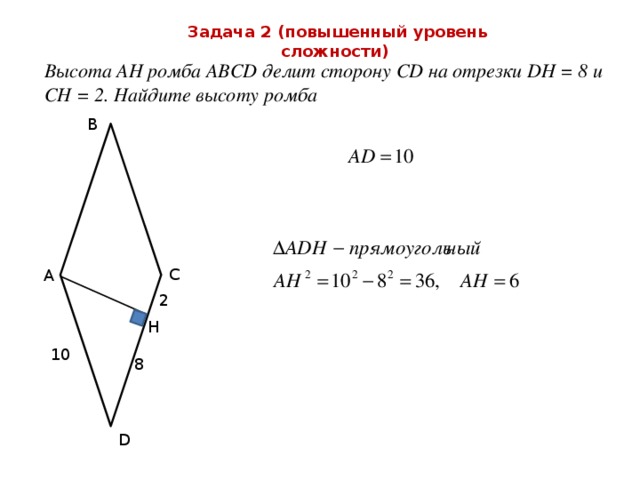
Задача 2 (повышенный уровень сложности)

Высота АН ромба АВСD делит сторону СD на отрезки DН = 8 и СН = 2. Найдите высоту ромба

В

С

А

2

Н

10

8

D

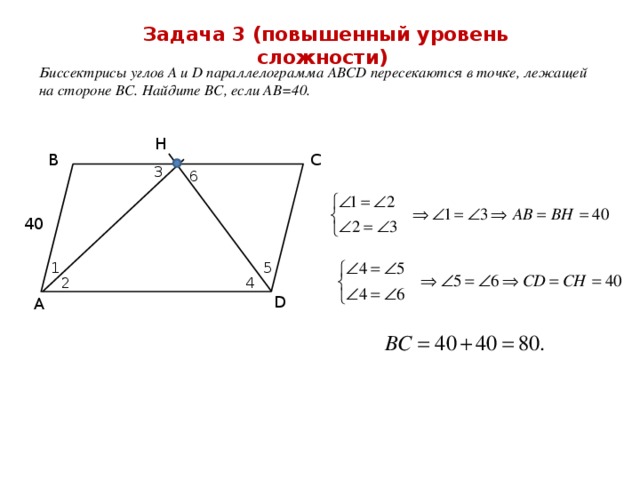
Задача 3 (повышенный уровень сложности)

Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке, лежащей на стороне ВС. Найдите ВС, если АВ=40.

Н

В

С

3

6

40

5

1

2

4

D

А

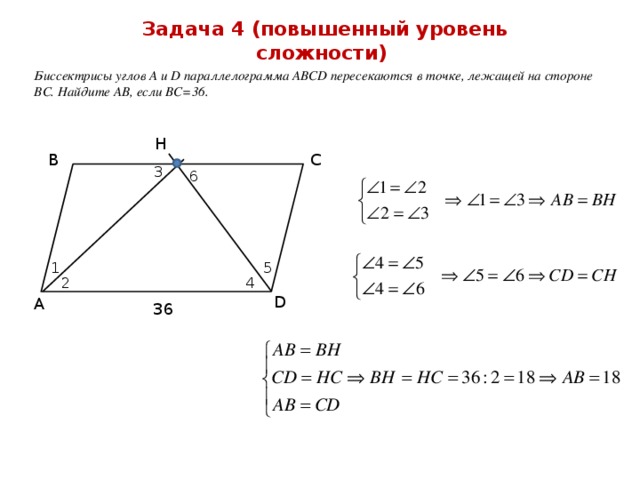
Задача 4 (повышенный уровень сложности)

Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке, лежащей на стороне ВС. Найдите AB, если BC=36.

Н

В

С

3

6

5

1

2

4

D

А

36

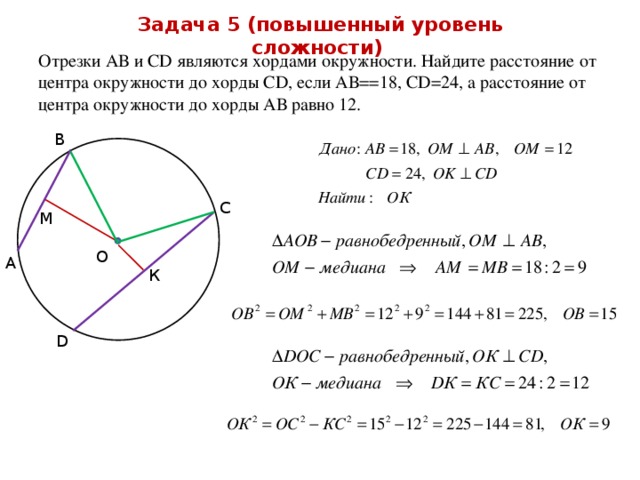
Задача 5 (повышенный уровень сложности)

Отрезки АВ и СD являются хордами окружности. Найдите расстояние от центра окружности до хорды СD, если АВ==18, СD=24, а расстояние от центра окружности до хорды АВ равно 12.

В

С

М

О

А

К

D

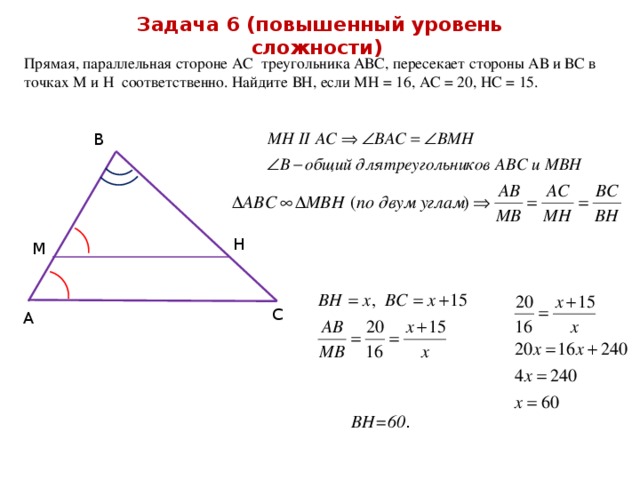
Задача 6 (повышенный уровень сложности)

Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и Н соответственно. Найдите ВН, если МН = 16, АС = 20, НС = 15.

В

Н

М

С

А

ВН=60 .

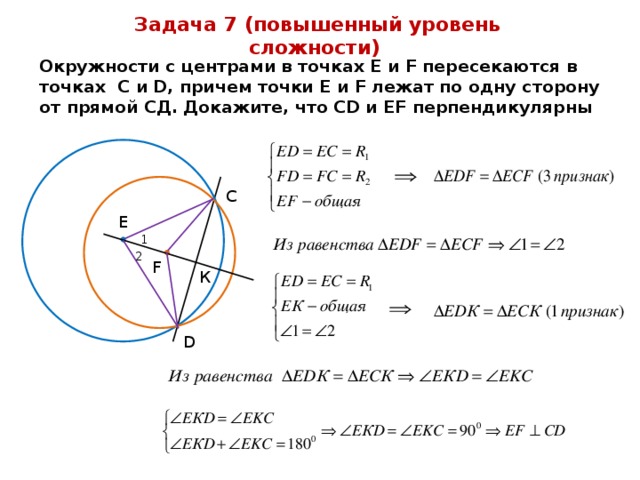
Задача 7 (повышенный уровень сложности)

Окружности с центрами в точках E и F пересекаются в точках C и D, причем точки E и F лежат по одну сторону от прямой СД. Докажите, что CD и EF перпендикулярны

С

E

1

2

F

К

D

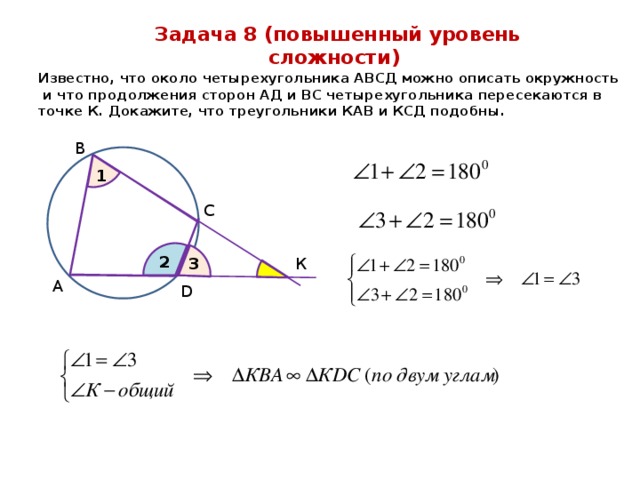
Задача 8 (повышенный уровень сложности)

Известно, что около четырехугольника АВСД можно описать окружность и что продолжения сторон АД и ВС четырехугольника пересекаются в точке К. Докажите, что треугольники КАВ и КСД подобны.

В

1

С

2

К

3

А

D

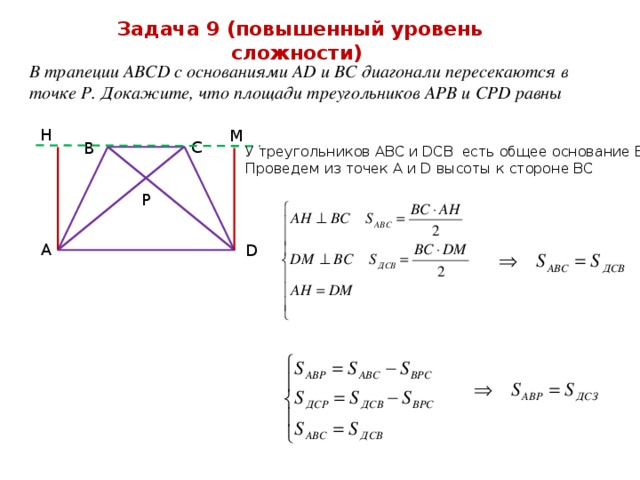
Задача 9 (повышенный уровень сложности)

В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке Р. Докажите, что площади треугольников АРВ и СРD равны

Н

М

С

В

У треугольников АВС и DСВ есть общее основание ВС

Проведем из точек А и D высоты к стороне ВС

Р

А

D

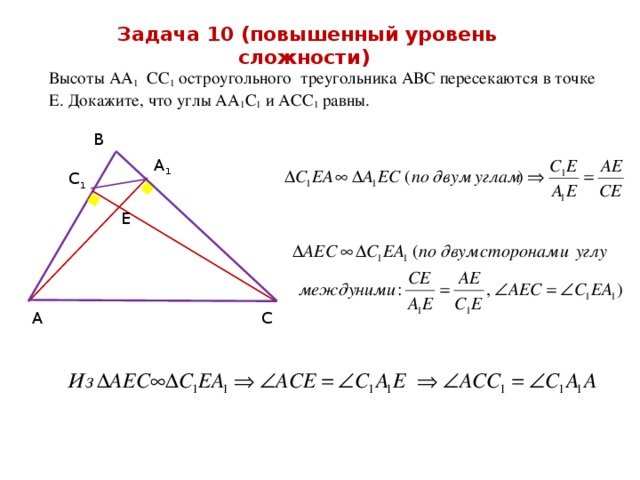
Задача 10 (повышенный уровень сложности)

Высоты АА 1 СС 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы АА 1 С 1 и АСС 1 равны.

В

А 1

С 1

Е

А

С

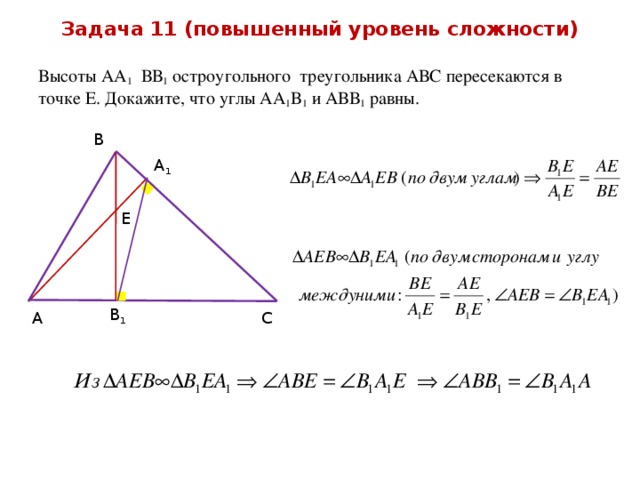
Задача 11 (повышенный уровень сложности)

Высоты АА 1 ВВ 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы АА 1 В 1 и АВВ 1 равны.

В

А 1

Е

В 1

А

С

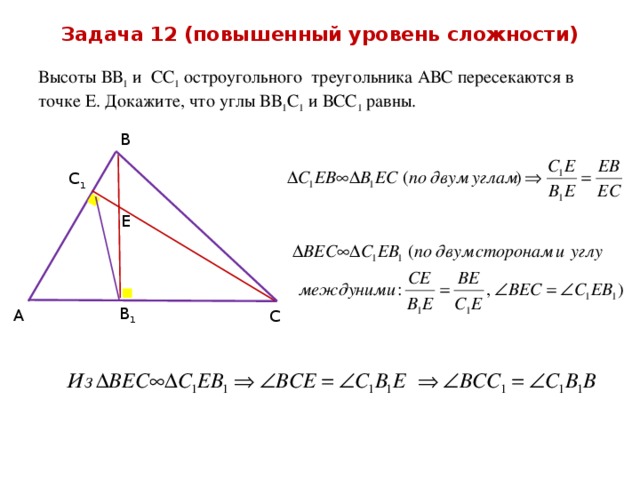
Задача 12 (повышенный уровень сложности)

Высоты ВВ 1 и СС 1 остроугольного треугольника АВС пересекаются в точке Е. Докажите, что углы ВВ 1 С 1 и ВСС 1 равны.

В

С 1

Е

В 1

А

С

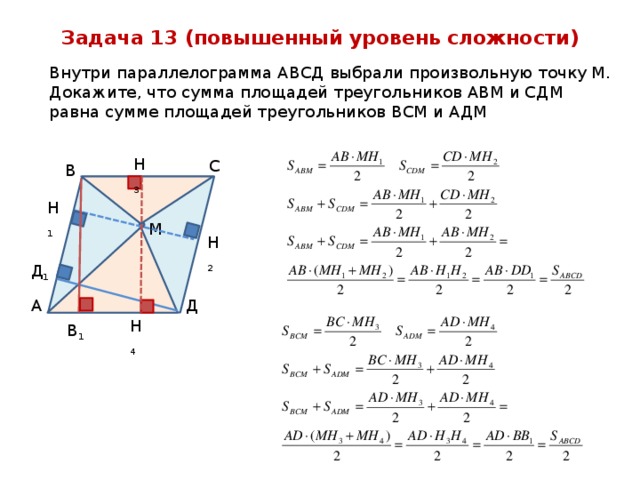
Задача 13 (повышенный уровень сложности)

Внутри параллелограмма АВСД выбрали произвольную точку М. Докажите, что сумма площадей треугольников АВМ и СДМ равна сумме площадей треугольников ВСМ и АДМ

Н 3

С

В

Н 1

М

Н 2

Д 1

Д

А

Н 4

В 1

Задача 14 (высокий уровень сложности)

Из вершины прямого угла С треугольника АВС проведена высота СР. Радиус окружности, вписанной в треугольник ВСР равен 60. Тангенс угла ВАС равен 4/3. Найдите радиус окружности, вписанной в треугольник АВС.

А

Р

5k

3k

3,2k

2,4k

С

4k

В

Задача 15 (высокий уровень сложности)

Биссектрисы углов А и В параллелограмма АВСД пересекаются в точке К. Найдите площадь параллелограмма, если ВС = 2, а расстояние от точки К до стороны АВ равно 1.

М

С

В

4

3

Н

К

1

2

Д

А

Р

Точки М, К и Р лежат на одной прямой, МР = КМ + КP = 2

Задача 16 (высокий уровень сложности)

В треугольнике АВС известны длины сторон АВ = 8, АС = 64. Точка О - центр окружности, описанной около треугольника АВС. Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д. Найдите СД.

В

О

А

Д

С

К

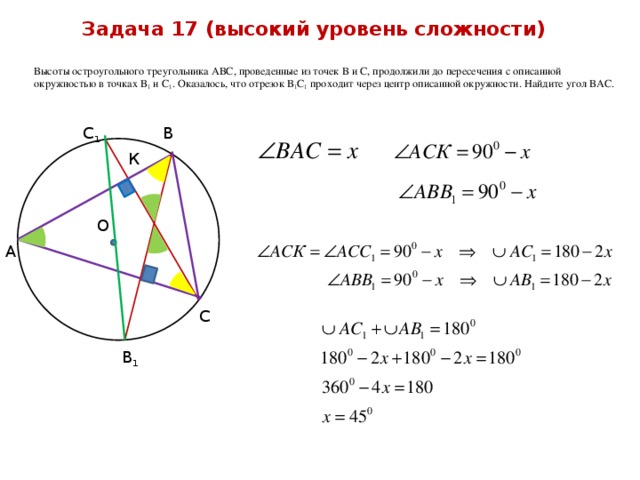
Задача 17 (высокий уровень сложности)

Высоты остроугольного треугольника АВС, проведенные из точек В и С, продолжили до пересечения с описанной окружностью в точках В 1 и С 1 . Оказалось, что отрезок В 1 С 1 проходит через центр описанной окружности. Найдите угол ВАС.

В

С 1

К

О

А

С

В 1

Задача 18 (высокий уровень сложности)

Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 33.

К

В

k

М

С

t

O

Р

А

Т

D

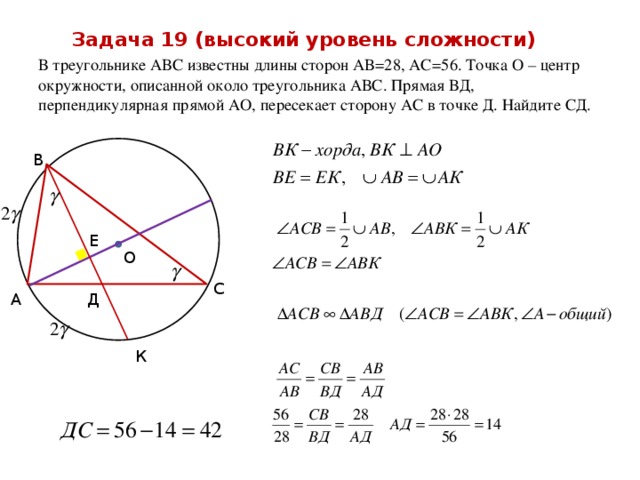
Задача 19 (высокий уровень сложности)

В треугольнике АВС известны длины сторон АВ=28, АС=56. Точка О – центр окружности, описанной около треугольника АВС. Прямая ВД, перпендикулярная прямой АО, пересекает сторону АС в точке Д. Найдите СД.

В

Е

О

С

Д

А

К

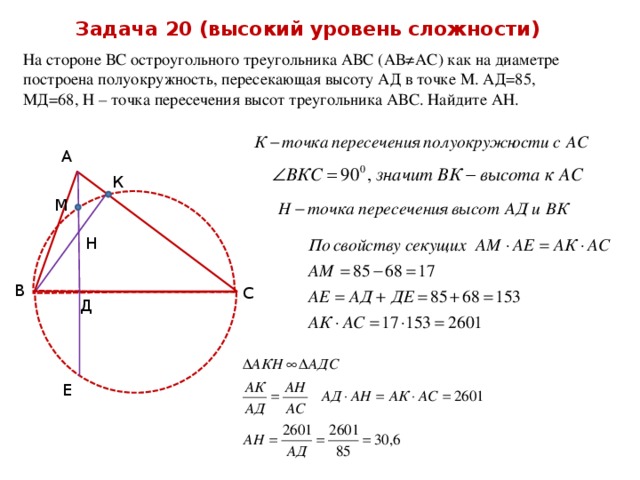
Задача 20 (высокий уровень сложности)

На стороне ВС остроугольного треугольника АВС (АВ≠АС) как на диаметре построена полуокружность, пересекающая высоту АД в точке М. АД=85, МД=68, Н – точка пересечения высот треугольника АВС. Найдите АН.

А

К

М

Н

В

С

Д

Е

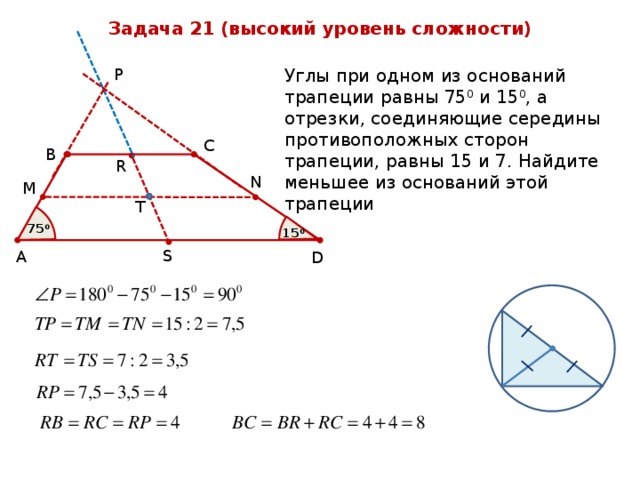
Задача 21 (высокий уровень сложности)

P

Углы при одном из оснований трапеции равны 75 0 и 15 0 , а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 7. Найдите меньшее из оснований этой трапеции

С

В

R

N

M

T

75 0

15 0

S

А

D