Гува Елена Александровна

Урок алгебры в 8 классе по теме «Иррациональные числа»

Цель: дать понятие об иррациональных числах и множестве действительных чисел.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Какие числа относятся к рациональным?

2. Запишите десятичную дробь в виде обыкновенной: а) 2,75; б) 0,(7); в) 0,(73).

3. Представьте в виде десятичной дроби число: а) 1/80; б) 5/17.

4. Найдите |3 · 2,8 - 11,6|.

Вариант 2

1. В каком виде записываются рациональные числа?

2. Запишите десятичную дробь в виде обыкновенной: а) 1,25; б) 0,(4); в) 0,(37).

3. Представьте в виде десятичной дроби число: а) 1/40; б) 3/13.

4. Найдите |2 · 3,7 - 10,9|.

III. Изучение нового материала (основные понятия)

Разумеется, кроме рациональных чисел существуют и другие числа.

Пример 1

Рассмотрим десятичную бесконечную дробь 0,10110111.... В этом числе после запятой выписана цифра 1, потом 0, затем 11, потом 0, далее 111, потом 0 и т. д.

Эта дробь является бесконечной и непериодической, т. к. количество единиц все время увеличивается. Поэтому в этой дроби нет повторяющихся групп цифр. Следовательно, такое число (по определению) не может быть рациональным. Подобные числа называют иррациональными (приставка «ир» означает «не»).

Таким образом, иррациональное число — десятичная бесконечная непериодическая дробь. Иррациональное число нельзя представить в виде отношения m/n и обратно: любое число, не представимое в виде m/n, является иррациональным.

Пример 2

Докажем, что сторона а квадрата с площадью 3 является иррациональным числом.

Докажем от противного. Предположим, что число a — рациональное, т. е. его можно представить в виде несократимой дроби (у которой числитель и знаменатель взаимно простые числа—по основному свойству дробей это всегда можно сделать, разделив числитель и знаменатель на их НОД). Тогда число a можно записать в виде a = m/n (n ≠ 1). Площадь квадрата со стороной а есть 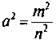 — несократимая дробь и не является натуральным числом (т. к. n2 ≠ 1 — натуральное число). С другой стороны, а2 = 3 — натуральное число. Поэтому получаем противоречие: одно и то же число а2 не может быть и несократимой дробью, и целым числом. Это противоречие свидетельствует о том, что число а не может быть рациональным, т. е. является числом иррациональным. Число а, которое является корнем уравнения а2 = 3, обозначают символом 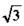. Таким образом, было доказано, что  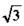— иррациональное число.

Иррациональные числа внешне могут иметь различный вид: 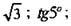 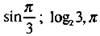(≈ 3,1416... — отношение длины окружности к ее диаметру) и т. д.

Рациональные и иррациональные числа называют действительными числами. Множество действительных чисел обозначают буквой R.

Например, 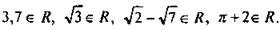 На диаграмме представлена структура множества действительных чисел.

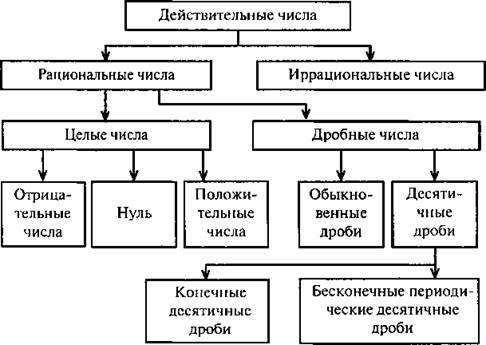
В математике приняты обозначения наиболее часто рассматриваемых множеств чисел:

множество натуральных чисел — N;

множество целых чисел — Z;

множество рациональных чисел – Q;

множество действительных чисел — R.

Изображение действительных чисел на числовой прямой Числовой осью называется прямая, на которой выбраны начало отсчета (точка нуль), положительное направление и масштаб.

Тогда каждому действительному числу на оси 0x отвечает определенная точка. При этом положительные числа откладывают справа от точки О, отрицательные числа — слева. Также справедливо и обратное утверждение: любой точке на оси ОХ отвечает определенное число.