Дата проведения:08.12.2021
Группа: 2-2
Преподаватель: Касымова У.Ш.
Тема урока: «Иррациональные уравнения».
Цель урока: дать понятие «иррациональные уравнения», обучить решению иррациональных уравнений возведением обеих его частей в одну и ту же натуральную степень.
Задачи:
Образовательная:
- дать понятие иррационального уравнения;
- научить решать иррациональные уравнения;
Развивающая:
- развитие внимания, познавательной активности, памяти, мышления; развивать навыки самостоятельного применения знаний в знакомой и измененной ситуации;
- учить анализировать, выделять главное, доказывать и опровергать логические выводы.
Воспитательная:
- формирование нравственных качеств, аккуратности, дисциплинированности, чувства собственного достоинства, ответственного отношения к достижению цели;
- формирование навыков коллективного труда.
Тип урока: урок усвоения новых знаний.
Ход урока
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель корня - четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (определение корня с четным показателем степени);
2) если показатель корня - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.
Пример 1. Решить уравнение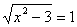
Решение.
Возведем обе части уравнения в квадрат.
x2 - 3 = 1;
Перенесем -3 из левой части уравнения в правую и выполним приведение подобных слагаемых.
x2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x1 = -2 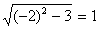 - истинно:
- истинно:
При x2 = -2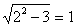 - истинно.
- истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
Пример 2. Решить уравнение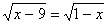 .
.
Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.
Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:
а) x - 9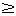 0;
0;
x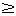 9;
9;
б) 1 - x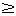 0;
0;
-x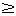 -1 ;
-1 ;
x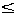 1.
1.
ОДЗ данного уранения: x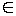
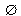 .
.
Ответ: корней нет.
5.закрепление
Решите уравнения (14 —25): 1. √ x=7 − x. О т в е т: 15 − √29 /2 .
2. √ x −1=3 − x. О т в е т: 2.
3. √ x2− x=2 x −3. О т в е т: 11+ √13 6 .
4. 2 √ (x −2)(4 − x)= x −2. О т в е т: 2;
5 . 18. √ 3x+1+ √ x=11. О т в е т: 16.
6. √ 2x2−2x=3 − √ x2− x −1. У к аз ан и е: сделайте замену x2− x =t. О т в е т: −1; 2.
7. √ 9− x − √ 4 − x=2. О т в е т: 6316 .
8. x − √ x+2=4. О т в е т: 7.
9. √ 3x −5− √ 4 − x=1. О т в е т: 3.
10. √ x2+20+ x2=22. О т в е т: −4; 4. 24
11. √ 2x2+8 x+7 − x=2. О т в е т: −1.
12. √ 2x − 4 − √ x+5=1. О т в е т: 20.
Подведение итогов.
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Дата проведения:9.12.2021
Группа: 2-2
Преподаватель: Касымова У.Ш.
Тема: Логарифмические уравнения
Цели урока:
- обеспечить закрепление новых понятий логарифмическое уравнение, методы решения логарифмических уравнений;
- развивать умение анализировать, сопоставлять, делать выводы, синтезировать полученные знания и умения;
- воспитывать умение работать в парах; навык самооценки и взаимооценки.
\Ход урока:
а) log28
б) log 327
в) log 232.
Что использовали для выполнения данного задания?
2. Найдите х:
а) log3 x = 4 (х=81)
б) ) log3 (7х-9)=log3x (х= 1,5)
Как иначе сформулировать 3 задание? (решите уравнение)
А как вы думаете, какие это уравнения? (логарифмические)
Запишем тему урока: «Логарифмические уравнения»
3.Объяснение нового материала
Записать на доске, поясняя
log аf(x) = log ag(x), где а-положит. число, отличное от 1, и уравнения, сводящиеся к этому виду.
Пример: log3 (7x – 9) = log3x
7х – 9 = х
6х = 9
х = 1,5
Применение формул потенцирования расширяет область определения уравнения. Поэтому необходима проверка корней. Проверим найденные корни по условиям 7х-90
Методы решения логарифмических уравнений
1. По определению логарифма.
Так решаются простейшие уравнения вида 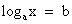 .
.
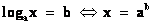
Рассмотрим № 514(а): Решить уравнение 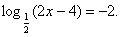
Как вы предлагаете его решать? (По определению логарифма)
Решение. 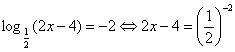 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.
Ответ: 4.
В этом задании 2х – 4 0, так как 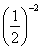 0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 0 в этом задании выписывать не надо.
0, поэтому посторонних корней появиться не может, и проверку нет необходимости делать. Условие 2х – 4 0 в этом задании выписывать не надо.
2. Потенцирование (переход от логарифма данного выражения к самому этому выражению).
Рассмотрим №519(г): log5(x2+8)-log5(x+1)=3log5 2
Какую особенность вы заметили? (Основания одинаковы и логарифмы двух выражений равны). Что можно сделать? (Потенцировать).
При этом надо учитывать, что любое решение содержится среди всех х, для которых логарифмируемые выражение положительны.
Решение: ОДЗ:
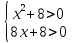
X2+80 лишнее неравенство
log5(x2+8) =log5 23+ log5(x+1)
log5(x2+8)= log5 (8 x+8)
Потенцируем исходное уравнение
x2+8= 8 x+8
получим уравнение x2+8= 8x+8
Решаем его: x2-8x=0
х=0, х=8
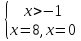
Ответ: 0; 8
В общем виде переходом к равносильной системе:
Уравнение 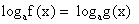
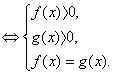
Закрепление
Каким методом будем находить корень уравнения? (по определению)
А) log0,1(x2+4x-20)=0 б) log1/7(x2+x-5)=- 1
x2+4x-20=0,10 x2+x-5=1/7- 1
x2+4x-20=1 x2+x-5=7
x2+4x-21=0 x2+x-12=0
x1+x2= -4 x1+x2= -1
x1*x2=-21 x1*x2=-12
x1=-7, x2= 3 x1=-4, x2= 3
№ 17.6 (а, б)
Каким методом будем решать? (потенцирования)
Решаем в парах
А) 3х-6=2х-3 б)14+4х=2х+2
3х-2х=-3+6 4х-2х=2-14
х=3 2х= - 12, х= - 6. корней нет
Самостоятельная работа
log 3 (2х - 1) = log 3 27
log 3 (4х+5)+log 3 (х +2) = log 3 (2х +3)
log 2 х = - log 2 (6х - 1)
4 + log 3(3-х) = log 3 (135-27х)
Итог урока:
Дайте определение логарифмического уравнения.
Какими методами можно решать логарифмические уравнения?
Домашнее задание.
log 3 x= 4
log 2 x= -6
logx 64 = 6
- log x64 = 3
2 log x8 + 3 = 0
uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу
Дата проведения:9.12.2021г
Предмет: математика
Группа: 2-2
Преподаватель: Касымова У.Ш.
Тема урока: рациональные неравенства
Цели урока:
образовательная: обобщить и систематизировать знания по теме «Дробно-рациональные неравенства»;
развивающая: развить внимание, логическое мышление, речь, познавательный интерес к предмету;
воспитательная: формирование коммуникативных умений, культуры общения, сотрудничества.
Ход урок
Рациональное неравенство — неравенство, левая и правая части которого являются дробно-рациональными функциями, то есть функциями, представимыми в виде отношения многочленов f(x) и g(x).
Стандартный вид рационального неравенства
f(x)g(x)0
Алгоритм решения рациональных неравенств
Переносим все в одну сторону и приводим к общему знаменателю, чтобы получить рациональное неравенство в стандартном виде: f(x)g(x)0;
Раскладываем числитель (f(x)) и знаменатель (g(x)) на множители. Для этого решаем уравнения f(x)=0 и g(x)=0;
Находим ОДЗ (g(x)≠0);
Отмечаем на числовой оси нули числителя и нули знаменателя;
Определяем знаки для каждого интервала. Для этого берем произвольный 𝑥 из одного из интервалов и определяем знак в интервале к которому относится корень, чередуем знаки, обращая внимание на корни, повторяющиеся в неравенстве несколько раз, от четности или нечетности количества раз их повторения зависит, меняется знак при прохождении через них или нет;
Выбираем интервалы, на которых значения функции имеют знак, соответствующий знаку неравенства;
Записываем ответ, обращая внимания на знак неравенства и на ОДЗ. Если неравенство строгое — все точки выколотые; если неравенство нестрогое — нули знаменателя — выколотые точки (по ОДЗ), а нули числителя — не выколотые точки.
Рациональные неравенства
Рациональные неравенства – это неравенства, обе части которых являются рациональными выражениями.
Что такое рациональное выражение? Напомню:
Рациональное выражение — это алгебраическое выражение, составленное из чисел и переменной x с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Например, такое рациональное неравенство: x+1/x−2≤x+2x
Решение всех рациональных неравенств сводится к двум основным шагам:
Шаг 1. Перенос. Общий знаменатель. Разложение на множители
Переносим все в одну сторону, приводим к общему знаменателю и раскладываем числитель и знаменатель на множители.
Все множители должны быть «линейными», то есть переменная в каждом из них – только в первой степени.
Если какой-то из множителей нелинейный, и его невозможно разложить на линейные, от него надо избавиться.
Пример №1
x/x−2≤1
xx−2≤1 ⇔ xx−2−1≤0 ⇔ x−x+2x−2≤0 ⇔ 2x−2≤0
Почему корень выколотый? Потому что он из знаменателя! x
4.Закрепление
Пример 2
x+1/x−2≤x+2x
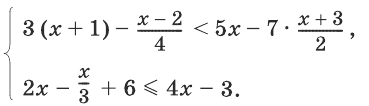
Пример: 4
Решить совокупность неравенств
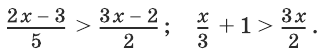
Решение:
Преобразовав каждое из неравенств, получим совокупность, равносильную заданной:
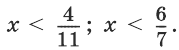 С помощью числовой прямой находим, что решением заданной совокупности является промежуток
С помощью числовой прямой находим, что решением заданной совокупности является промежуток 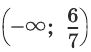 (рис. 1.115) (объединения заштрихованных на рис. 1.115. промежутков).
(рис. 1.115) (объединения заштрихованных на рис. 1.115. промежутков).

Дробно-линейные неравенства — это неравенства вида 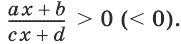
Пример 1.
Решить неравенство 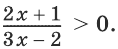
Итог урока. uma.kasymova@mail.ru
Указать дату, Ф.И.О и группу






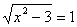
 - истинно:
При x2 = -2
- истинно:
При x2 = -2 - истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
- истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.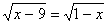 .
. 0;
0; 1.
1.
 .
.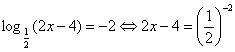 , Отсюда 2х – 4 = 4; х = 4.
, Отсюда 2х – 4 = 4; х = 4.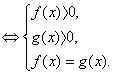
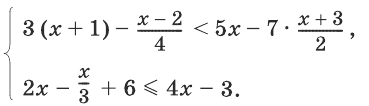
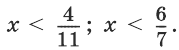 С помощью числовой прямой находим, что решением заданной совокупности является промежуток
С помощью числовой прямой находим, что решением заданной совокупности является промежуток 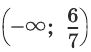 (рис. 1.115) (объединения заштрихованных на рис. 1.115. промежутков).
(рис. 1.115) (объединения заштрихованных на рис. 1.115. промежутков).










