Использование Кругов Эйлера при решении задач

Использование Кругов Эйлера при решении задач

Круги Эйлера – это геометрическая схема, которая помогает находить и/или делать более наглядными логические связи между явлениями и понятиями. А также помогает изобразить отношения между каким-либо множеством и его частью.

Автор метода - ученый Леонард Эйлер (1707-1783). Он так и говорил о названных его именем схемах: «круги подходят для того, чтобы облегчить наши размышления». Эйлер считается немецким, швейцарским и даже российским математиком, механиком и физиком. Он много лет проработал в Петербургской академии наук и внес существенный вклад в развитие российской науки.

Задача. В классе 32 человека. Из них 14 играют в баскетбол, 24 - в пионербол, 16 - в волейбол. Увлекаются двумя видами спорта - баскетболом и пионерболом - шестеро, баскетболом и волейбол - четверо, пионерболом и волейболом - четверо. Трое ни чем не занимаются. Сколько ребят увлекается всеми видами игры?

Решение.

Для решения используем Круги Эйлера.

Внутри большего круга, изображающего множество всех учеников класса, поместим три меньших круга, означающих соответственно множества учеников увлекающимися баскетболом, пионерболом и волейболом (см. рис.).

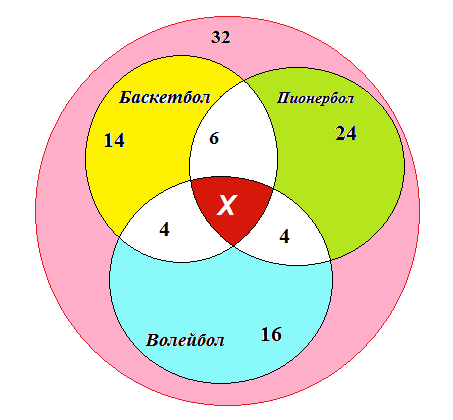
Пусть х – человек увлекается всеми видами игры (обозначено х и фон красный), тогда

32 – 3 = 29 (ч. ) – играют хотя бы в одну игру.

14 – 6 – 4 - х = 4 - х (ч. ) – играют только в баскетбол.

24 – 6 – 4 - х=14 - х (ч. ) – играют только в пионербол.

16 – 4 – 4 – х = 8 - х (ч. ) – играют только в волейбол.

4 – х + 14 - х + 8 - х + 5 + 6 + 4 = 29 (ч. )

41 - 3 х =29

х = 4

Ответ: четыре человека увлекаются всеми тремя видами спорта.