
Муниципальное бюджетное общеобразовательное учреждение «Ушаковская средняя общеобразовательная школа» МАТЕМАТИКА В КАЛЕНДАРЕ
Выполнила: Верхотурова В.А.
ученица 8 класса
Руководитель: Гегельская Е.В.
учитель математики

Актуальность исследования
Интерес к настенному календарю у нас появился после задачи, которую нам предложил учитель на уроке геометрии, при изучении темы «Прямоугольные треугольники»: «если соединить числа 10,20, и 30 января 2006 года, то получится равнобедренный прямоугольный треугольник. Докажите это.» Задача про календарь и треугольники оказалась нестандартной задачей на признаки равенства треугольников и вызвала у большинства учащихся интерес и много вопросов. По совету учителя мы продолжили исследование задачи и постарались ответить на возникшие вопросы. Результатом моего исследования стал проект «Математика в календаре».

Цель проекта: Доказать задачу про календарь и треугольники, а также найти другие задачи, для решения которых используется календарь.
Задачи проекта:
1. Изучить литературу по данной теме.
2. Обработать полученную информацию.
3. Познакомиться с историей появления календарей.
4. Исследовать задачу про календарь и треугольники.
5. Подобрать и исследовать задачи по теме «календари».
6. Выявить какими особенностями обладают календари.

Исследование задачи про календарь и треугольники Задача: Если в календаре на январь 2006 года соединить числа 10, 20. 30, то получим равнобедренный прямоугольный треугольник. Доказать.
Очевидно, что у треугольника 30 – 9 – 10 угол 9 прямой, и, аналогично, является прямым угол 13 у треугольника
10 – 13 – 20. Ясно, что стороны 9 -30 и
10 – 13 равны; аналогично равны стороны 9 – 10 и 13 – 20. Поэтому треугольники 9 – 30 – 10 и 13 – 10 – 20 равны по двум сторонам и углу между ними. Значит, отрезки 10 – 30 и 10 – 20 равны. Так как сумма углов в треугольнике равна 180˚, получаем, что сумма острых углов в треугольнике 9 – 10 – 30 равна 180˚–90˚=90˚. Следовательно, сумма углов, дополняющих угол 10 треугольника 10-20-30 до развернутого угла, равна сумме острых углов треугольника 9 – 10 – 30. Значит, угол 10 тоже равен 90˚. Итак, треугольник 10 – 20 – 30 является равнобедренным прямоугольным.
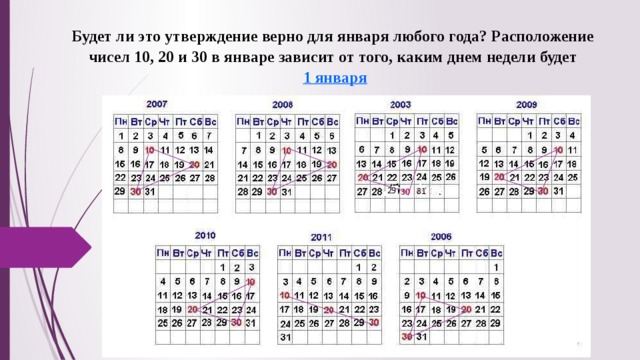
Будет ли это утверждение верно для января любого года? Расположение чисел 10, 20 и 30 в январе зависит от того, каким днем недели будет 1 января
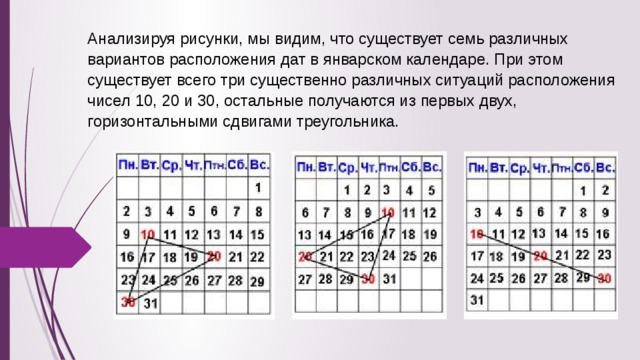
Анализируя рисунки, мы видим, что существует семь различных вариантов расположения дат в январском календаре. При этом существует всего три существенно различных ситуаций расположения чисел 10, 20 и 30, остальные получаются из первых двух, горизонтальными сдвигами треугольника.

Вывод: Табель – календари обладают следующей особенностью:
- Если соединить числа 10, 20 и 30 в январе месяце любого года, то будет получаться равнобедренный прямоугольный треугольник (за исключением тех мест, где центры клеток 10, 20 и 30 лежат на одной прямой).
- Заметили, что первая ситуация получается, если 1 число месяца приходится на воскресенье, понедельник и вторник.
- Вторая ситуация получается, если 1 число месяца приходится на среду, четверг и пятницу. Если 1 число приходится на субботу, то получаем, что числа 10, 20 и 30 лежат на одной прямой.
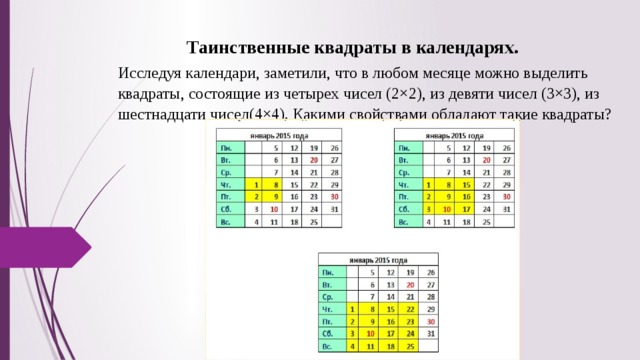
Таинственные квадраты в календарях.
Исследуя календари, заметили, что в любом месяце можно выделить квадраты, состоящие из четырех чисел (2×2), из девяти чисел (3×3), из шестнадцати чисел(4×4). Какими свойствами обладают такие квадраты?

Квадрат 2×2
Сумма чисел на одной диагонали выделенного квадрата, равна сумме чисел на другой диагонали. Чтобы найти сумму всех четырех чисел достаточно сумму чисел одной диагонали умножить на 2. (8+16) ×2=48
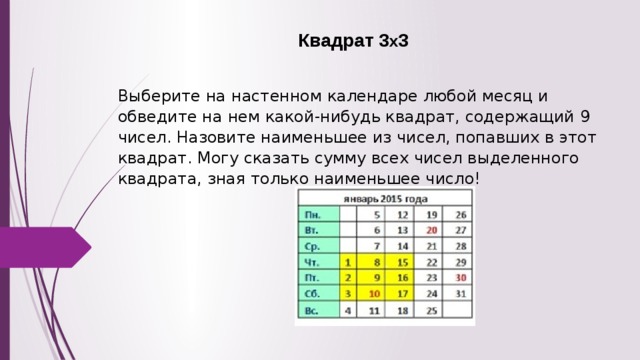
Квадрат 3 х 3
Выберите на настенном календаре любой месяц и обведите на нем какой-нибудь квадрат, содержащий 9 чисел. Назовите наименьшее из чисел, попавших в этот квадрат. Могу сказать сумму всех чисел выделенного квадрата, зная только наименьшее число!

Квадрат 4 х 4
Выберите на настенном календаре любой месяц и обведите на нем какой-нибудь квадрат, содержащий 16 чисел (4х4). Назовите наименьшее из чисел, попавших в этот квадрат. Могу сказать сумму всех чисел выделенного квадрата, зная два числа, стоящих на противоположных концах любой диагонали, обведенного квадрата!

МАТЕМАТИЧЕСКИЕ ЗАДАЧИ В КАЛЕНДАРЕ
1. Может ли быть в одном месяце 5 понедельников и 5 четвергов? Обоснуйте ответ.
Если в месяце 31 день, и он начинается с понедельника, то в нём может быть 5 понедельников, 5 вторников и 5 сред, но остальных дней недели по четыре, так как 5+5+5+4+4+4+4=31. Ответ: не может.
2. Может ли в феврале високосного года быть 5 понедельников и 5 вторников? Ответ обоснуйте.
Только в феврале високосного года может быть 5 понедельников и по 4 остальных дней недели, т.е. в сумме – 29 дней . Ответ: не может.
3. Известно. Что 1 декабря приходится на среду. На какой день недели приходится 1 января следующего года?
Среда 1, 8, 15, 22, и 29 декабря, четверг 30, пятница 31. Ответ: суббота 1 января следующего года.

ВЫВОДЫ В ходе работы над проектом я пришла к следующим результатам:
1· Доказала, что если соединить в табель – календаре в январе месяце любого года числа 10, 20 и 30, то получится равнобедренный прямоугольный треугольник (кроме месяца, когда 1 число приходится на субботу);
2· Показала, что в календаре можно выделять квадраты чисел 2×2; 3×3; 4×4, и применить правила быстрого подсчета суммы чисел в этих квадратах.
3· Решила и исследовала задачи, которые можно предлагать на уроках математики и во внеклассной работе.

Спасибо за внимание!































