Исследовательская работа "Шахматы и математика"

Шахматы и математика

Шахматы требуют колоссальной человеческой мысли, глубокий и большой расчет вариантов. Много родственного в шахматах с математикой, комбинаторикой, с моделями современного программирования. Особенно с математикой. Для победы в шахматы необходимо логически мыслить, просчитать комбинации на несколько ходов вперёд и быть предельно внимательным. И в науке математике не обойтись без логики и точного расчёта. Отсюда вытекает, что форма мышления математика и шахматиста довольно близки, а математические способности нередко сочетаются с шахматными. Мы заинтересовалась этой темой потому, что нам нравится играть в шахматы,  а так же предмет математика.

 Цель: найти и разобрать связь между шахматами и математикой, воспользоваться этой связью при решении математических задач.

Задачи:

- познакомиться с историей шахмат

- узнать что такое шахматные закономерности

- исследовать связь математики и шахмат

- рассмотреть математические решения задач, связанных с шахматной доской

- рассмотреть математические решения задач, связанных с шахматными фигурами.

Методы исследования: теоретический и эмпирический.

Теоретический метод позволил узнать историю возникновения шахмат, виды задач с шахматным содержанием и расширить знания в этой области математики и шахмат.

Эмпирический метод дал возможность разобрать методы решения задач, сюжетом которых являются шахматы.

В результате работы над проектом мы доказали что существует связь между шахматами и математикой, воспользовались этой связью при решении математических задач.

Научная статья

Введение

Среди крупных ученых известно немало сильных шахматистов: математик академик А. А. Марков, физик академик П. Л. Капица. В то же время многие гроссмейстеры имеют математическое или близкое к нему образование. Склонность к занятиям математикой проявлялась даже у чемпионов мира по шахматам. Первый советский чемпион мира М. Ботвинник в последние годы все силы отдал разработке алгоритма игры в шахматы и, по существу, переквалифицировался в математика - прикладника. Шахматы – одна из наиболее удобных моделей, используемых при разработке методов программирования. Разработка шахматных алгоритмов и компьютерных программ занимались и занимаются многие математики в разных странах. Еще одна точка соприкосновения математики и шахмат – это один из популярных жанров занимательной математики, к которому относятся математические задачи, игры и развлечения на шахматной доске. Этот жанр называется шахматной математикой. Например, многие шахматные термины используют математические названия: правило квадрата, правило треугольника, центр, симметрия. Выдающийся английский математик Г.Харди, проведя параллель между этими двумя видами человеческой деятельности в статье «Исповедь математика» заметил, что решение проблем шахматной игры есть не что иное, как математическое упражнение, а игра в шахматы это как бы насвистывание шахматных мелодий.

Эта игра привлекает нас тем, что для победы необходимо логически мыслить, просчитывать комбинации на несколько ходов вперед и быть предельно внимательным. Также мы заметили, что и в науке математике не обойтись без логики и точного расчета. А взаимосвязаны ли игра и наука, шахматы и математика? Если связаны, то как? И есть ли в игре что-то от науки, а в науке от игры? На эти вопросы мы и попытаемся ответить в своей работе.

Проблема. В подростковом возрасте познавательный интерес к математике уменьшается, в результате качество знаний снижается. Но ученикам всегда нравиться играть, а шахматы предоставляют такую возможность.

Гипотеза. Решение шахматно - математических задач, возможно, будет способствовать расширению кругозора в области математики и шахмат, повысит познавательную активность.

Актуальность данной темы заключается в привлечении учащихся к решению логических математических задач, повышении их интереса к математике.

Новизна работы заключается в том, что тема математики и шахмат недостаточно освещена в современной литературе. По этой проблеме было найдено небольшое количество книг. 

Практическая значимость работы состоит в том, что задачи с применением шахматной теории часто встречаются на олимпиадах по математике. Данное исследование будет полезным для учащихся, интересующихся математикой и шахматами. Материалы данной работы могут быть использованы в работе кружка «Шахматы» как информационно - практический материал.

1. История возникновения шахмат

История шахматной игры давно уже пробудила к себе интерес многих людей на планете, но о ней мы, тем не менее, знаем очень немного. Существует несколько легенд относительно возникновения этой игры, но их историческая правда заключается лишь в том, что они правильно называют местом возникновения Азию, а временем возникновения – очень далекое прошлое. Древнеегипетское искусство донесло до нас изображения игр, похожих на шахматы. Найдены были также документы, относящиеся к шахматам и написанные свыше тысячи лет назад. Однако шахматная игра той эпохи не была тождественна современной. На протяжении своей истории шахматы, несомненно, претерпели многочисленные изменения, и, кто знает, не является ли предком наших шахмат игра в шашки, или, точнее, некоторое подобие игры.

Рис. 1

В Древнюю Русь шахматная игра проникла с Востока (предположительно, каспийско-волжским путём) не позднее VIII-IX веках. Это подтверждается археологическими находками и лингвистическими данными: русские термины «шахматы», «слон», «ферзь» — восточного происхождения. Одним из крупнейших центров шахматной игры в XII—XV вв. был Новгород, где при раскопках шахматные фигурки обнаружены во многих усадьбах и домах, принадлежавших представителям различных слоёв городского населения. Упоминания о шахматах часто встречаются и в русском героическом эпосе.

Несмотря на то, что церковь до середины XVII в. вела упорную борьбу по искоренению шахмат на Руси как «бесовских игрищ», они были популярны среди ремесленников, торговцев, служилых людей, бояр. Шахматами увлекались Иван Грозный, по одной из версий скончавшийся за шахматной партией, Борис Годунов, Алексей Михайлович и другие государственные деятели.

В начале XVIII в. распространению шахмат в России способствовал Пётр I, который был большим любителем игры и вводил её на ассамблеях. В шахматы играли А. Меншиков, Г. Потёмкин, А. Суворов, Екатерина II.

Рис.2

2. Связь между шахматами и математикой

В первую очередь попробуем найти эту связь. Для этого мы   рассмотрим шахматную доску. Итак,  мы видим, что на шахматной доске есть координаты,  также на ней есть и симметрия,  геометрия тоже не обошла её стороной (Рис.3).

Рис.3. Шахматная доска

Основываясь на этом, я начал рассматривать эту связь более подробно, а именно на примерах.

2.1. Симметрия в шахматах

Симметрия, как общий принцип гармонии в живой природе имеет глубокий смысл. Изучение ее проявлений, закономерностей играет важную роль в математике, физике, химии, биологии.

Если каждую точку данной фигуры сместить каким-нибудь образом, то мы получим новую фигуру. Говорят, что эта фигура получена преобразованием из данной. Рассмотрим примеры преобразования фигур.

Симметрия относительно точки – центральная симметрия

Пусть F – данная фигура и О – фиксированная точка плоскости. Преобразование фигуры F в фигуру F₁, при котором ее каждая точка Х переходит в точку Х₁, симметричную относительно данной точки О, называют преобразованием симметрии относительно точки О (Рис. 4).

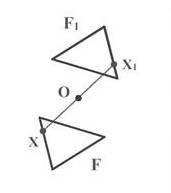
Рис. 4. Симметрия относительно точки

Симметрия относительно прямой – осевая симметрия

Преобразование фигуры F в F₁, при котором каждая точка Х  переходит в точку Х₁, симметричную относительно прямой g, называется преобразованием симметрии относительно прямой g. При этом фигуры F и F₁ называются симметричными относительно прямой g (Рис. 5).

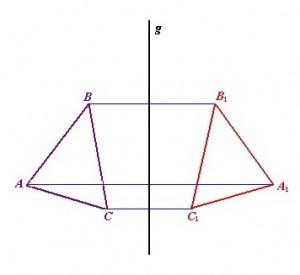
Рис. 5. Симметрия относительно прямой

Разнообразные мотивы симметрии встречаются и на шахматной доске. С одной стороны, речь может идти о симметрии естественной, т. е. возникающей в процессе шахматной партии, а с другой стороны, — используемой в шахматных задачах и этюдах.

Симметрия бывает различных типов; наиболее распространенные – осевая и центральная. На шахматной доске при осевой симметрии осью служит прямая, разделяющая левый и правый фланги доски (граница между вертикалями «d» и «e») или  нижнюю и верхнюю части (граница между четвертой и пятой горизонталями). Если, скажем, белый конь стоит на с2, а черный на с7 (Рис.6), то мы говорим, что эти кони расположены  симметрично. Осями являются и большие диагонали.

Рис. 6. Симметричное расположение коней на шахматной доске

Симметрией обладает исходное расположение шахматных фигур.Известна такая забавная история. Некто  явился в шахматный клуб и объявил,  что нашел верный способ не проигрывать черными. «Каким образом?» — спросили его.  «Очень просто, — ответил гость, — повторяя ходы противника!» Сыграть с наивным изобретателем вызвался  С.Ллойд, который и объявил ему мат в 4 хода.  Неясно, как Ллойд это сделал. Я могу поставить мат за 6 ходов при полной симметрии фигур.

1. с2-с3                                  с7-с6

2. е2-е3                                  е7-е6

3. Кg1-е2                               Кg8-е7

4. Кb1-с3                               Кb8с6

5. Кс3-е4                               Кс6-е5

6. Ке4-d6х

2.2. Система координат

Более чем за 100 лет до н.э. греческий ученый Гиппарх предложил опоясать на карте земной шар параллелями и меридианами и ввести хорошо теперь известные географические координаты: широту и долготу – и обозначить их числами.

В ХIVв. Французский математик Н. Оресм ввел, по аналогии с географическими, координаты на плоскости. Он предложил покрыть плоскость прямоугольной сеткой и называть широтой и долготой то, что мы теперь называем абсциссой и ординатой.

Это нововведение оказалось чрезвычайно продуктивным. На его основе возник метод координат, связавший геометрию с алгеброй. Основная заслуга в создании метода координат принадлежит французскому математику Р. Декарту.

Декартовая система координат на плоскости задается взаимно перпендикулярными координатными прямыми с общим началом в точке О и одинаковым масштабом. 

Точка О называется началом координат. Горизонтальная прямая называется осью абсцисс или осью х, вертикальная – осью ординат или осью у. Координатную плоскость обозначают хОу. Координаты точки обычно указывают в скобках рядом с обозначением точки: Р(х;у) ( Рис.7).

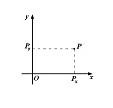
Рис. 7. Декартова система координат

На шахматной доске тоже есть координаты. При профессиональной игре, обычно, ведут записи (обозначение фигур и координаты этих фигур).

На рисунке 8 мы видим, некий алгоритм определения координат чёрного короля.

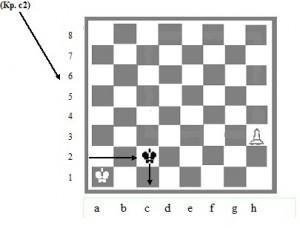
Рис.8. Определение координат шахматных фигур

2.3.Четность и нечетность

Число – одно из основных понятий математики, позволяющее выразить результаты счета или измерения.  Со временем люди научились не только называть числа, но и обозначать их цифрами (условные знаки для обозначения чисел).

Цифры 2, 4, 6, 8 называются четными,  а цифры 1, 3, 5, 7, 9  нечетными. Из признака делимости на 2 следует, что натуральные числа, которые делятся на 2, называются четными, остальные – нечетными.

На шахматной доске так же есть  чётность и нечётность. Тут они связаны с номером хода.

При каждом ходе король меняет четность хода. Например, первый ход

нечётный, второй – чётный и т.д. (Рис. 9)

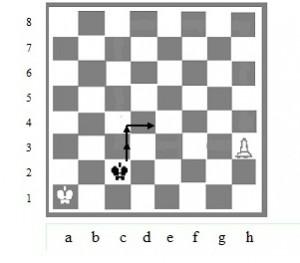
Рис. 9. Четность и нечетность на шахматной доске

Чётность, нечётность на шахматной доске ещё раз подтверждают прямое отношение шахмат к математике.

2.4. Геометрия шахматной доски

Можно сказать, что ничего удивительного и интересного здесь нет. Можно подумать,  что при виде шахматной доски мы сразу вспоминаем геометрию (из – за геометрической формы доски). Это, безусловно, так, но геометрическая форма ещё не всё.

Дело в том, что при игре в шахматы, как и в любой другой науке, есть свои определённые правила. И существует такое правило, как правило, квадрата.

Квадратом называется прямоугольник,  у которого все стороны равны.   При этой композиции (Рис.10) неопытные шахматисты рассуждают так: пешка идет сюда, король туда, пешка сюда, король туда и т.д. и при этом они часто путаются и, в конце концов, просчитываются.

13

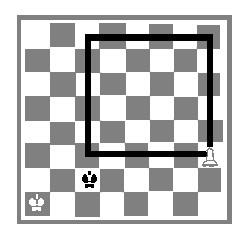
Рис. 10. Правило квадрата

Однако исход партии легко оценить при помощи «правила квадрата».

Достаточно выяснить, может ли король при своем ходе попасть в квадрат пешки. Итак,  в нашей композиции черные при ходе делают ничью (попадают в квадрат), а при ходе противника проигрывают.

3. Математические задачи на шахматную тему

3.1. Задачи на раскрашивание шахматной доски

Задача 1. Художник-авангардист Змий Клеточкин покрасил несколько клеток доски размером 8х8, соблюдая правило: каждая следующая закрашиваемая клетка должна соседствовать по стороне с предыдущей закрашенной клеткой, но не должна — ни с одной другой ранее закрашенной клеткой. Ему удалось покрасить 36 клеток. Побейте его рекорд!

Рис.11 Рис.12

Решение: Можно закрасить 42 клетки, закрасить 43 клетки невозможно. Примеры ответов изображены на рисунках.

Задача 2. Отметьте на доске 8х8 несколько клеток так, чтобы любая (в том числе и любая отмеченная) клетка граничила по стороне ровно с одной отмеченной клеткой.

Рис.13

Задача3. В квадрате 7х7 клеток закрасьте некоторые клетки так, чтобы в каждой строке и в каждом столбце оказалось ровно по три закрашенных клетки.

Рис.14 Рис.15

Вывод: при решении задач на раскрашивание шахматной доски нет какого-то определенного используемого математического метода, нужно просто быть внимательным при решении, чтобы учесть все содержащиеся в условии задачи ограничения.

Задача 4. Поля клетчатой доски размером 8х8 будем по очереди закрашивать в красный цвет так, чтобы после закрашивания каждой следующей клетки фигура, состоящая из закрашенных клеток, имела ось симметрии. Покажите, как можно, соблюдая это условие, закрасить: а) 26; б) 28 клеток. (В качестве ответа расставьте на тех клетках, которые должны быть закрашены, числа от 1 до 26 или до 28 в том порядке, в котором проводилось закрашивание.)

3.2. Задачи на разрезание шахматной доски

Среди математических задач и головоломок о шахматной доске наиболее популярны задачи на разрезание доски.

В математических задачах и головоломках на шахматной доске дело, как правило, не обходится без участия фигур. Однако доска сама по себе также представляет достаточно интересный математический объект. Поэтому рассказ о шахматной математике я начну с задач о шахматной доске. Прежде всего уместно привести одну гипотезу, использующую некоторые математические свойства доски. Согласно этой гипотезе шахматы произошли из так называемых магических квадратов. Магический квадрат порядка n представляет собой квадратную таблицу n х n, заполненную целыми числами от 1 до n² и обладающую следующим свойством: сумма чисел каждой строки, каждого столбца, а также двух главных диагоналей одна и та же. Для магических квадратов порядка 8 она равна 260 .

Рис.16

Закономерность расположения чисел в магических квадратах придает им волшебную силу искусства. Среди математических задач и головоломок о шахматной доске наиболее популярны задачи на разрезание доски. Первая из них также связана с легендой.

Задача 1. Один восточный властелин был таким искусным игроком, что за всю жизнь потерпел всего четыре поражения. В честь своих победителей, четырех мудрецов, он приказал вставить в его шахматную доску четыре алмаза — на те поля, на которых был заматован его король (см. рис.17), где вместо алмазов изображены кони). После смерти властелина его сын, слабый игрок и жестокий деспот, решил отомстить мудрецам, обыгравшим его отца. Он велел разделить им шахматную доску с алмазами на четыре одинаковые по форме части так, чтобы каждая заключала в себе по одному алмазу. Хотя мудрецы выполнили требование нового властелина, он все равно лишил их жизни. Эта задача о разрезании доски часто встречается в занимательной литературе.

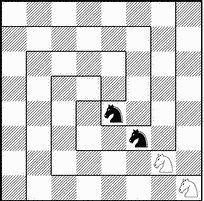
Рис.17

Задача 2. Сколько нужно провести разрезов на доске, чтобы пересечь все ее поля? Разумеется, восьми разрезов вполне достаточно — по одному вдоль каждой вертикали или каждой горизонтали. Однако, оказывается, что и семь прямых могут пересечь все 64 поля доски. Для этого одну прямую нужно провести почти в диагональном направлении через центр доски, а шесть других — в направлениях почти параллельных второй диагонали доски.

Рис.18 Семь прямых пресекают все поля доски

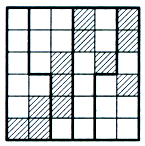
Задача 3. Разрежьте изображённую на рисунке 8,а доску на 4 одинаковые части, чтобы каждая из них содержала 3 заштрихованные клетки.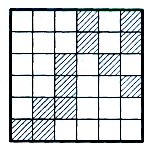

Задача 4. На какое максимальное число частей можно разрезать шахматную доску, если считать разными части, отличающиеся своей формой или цветом полей при совмещении.

Решение: Максимальное число частей равно 18. На рис.10 представлены два разреза. Решение на рис.10,а принадлежит Лойду; особенность его состоит в том, что одна из частей содержит восемь полей (максимум). В решении на рис.10,б, отличающемся внешней симметрией, ни одна часть не содержит более пяти полей. На рис.10,а части 17 и 18, или 8 и 9, хотя и имеют одинаковую форму, отличаются цветом полей при совмещении. Другие части, например, 3 и 6, вообще не могут быть совмещены (переворачивать их нельзя).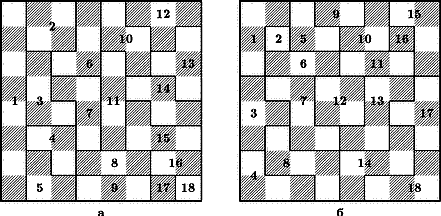

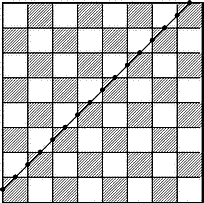
Рис. 10а. Решение Лойда. Рис. 10б. Другое решение

Задача 5. Какое максимальное число полей доски можно пересечь одним разрезом?

Решение: Поля доски образуются в результате пересечения 18 прямых – девяти вертикальных и девяти горизонтальных. С каждой из них прямая-разрез может пересечься лишь в одной точке, но из четырех прямых, образующих края доски, она пересекается лишь с двумя. Отсюда следует, что наша прямая пересекает прямые, образующие поля доски, самое большее в 16 точках. Эти точки разбивают прямую не более чем на 15 отрезков, каждый из которых заключен внутри какого-нибудь поля. Таким образом, любой разрез доски пересекает не более 15 полей. Из рис.11 следует, что ровно столько полей пересекает разрез, проведенный параллельно диагонали доски и проходящий через середины сторон двух угловых клеток.

Рис. 11

Вывод: задачи на раскрашивание и разрезание доски, по-моему, самые легкие математические шахматные задачи. Для решения таких задач единого алгоритма нет, нужны небольшие математические расчеты, хорошее внимание и, конечно, строгие логические рассуждения.

3.3. Задачи на нахождение числа фигур на шахматной доске, числа путей передвижения фигур

Рассмотрим задачи, связанные с шахматными фигурами.

Король – самая медленная фигура в шахматах. С любого места он может переступать только на соседние поля доски. Однако необычное измерение расстояний на доске лучше всего иллюстрирует движущийся король.

Задача 1. Какое максимальное число королей можно расставить на доске так, чтобы они не угрожали друг другу, т.е. не стояли рядом?

Решение: Разобьем доску на 16 квадратов. Если мы хотим, чтобы короли не касались друг друга, то, очевидно, в каждом из этих квадратов надо поместить не более одного из них. Это означает, что больше шестнадцати королей, удовлетворяющих условию задачи, расставить невозможно. Итак, максимальное число мирных королей на доске 8х8 равно 16.

Рис.19

Ладья – строгая, прямолинейная фигура. Она тоже часто встречается в математических задачах.

Задача 2. Какое наименьшее число поворотов должна сделать ладья при обходе всех полей доски nхn?

Решение: Ладья должна была сделать хотя бы один ход вдоль каждой вертикали или вдоль каждой горизонтали. Пусть, ладья двигалась хотя бы раз вдоль каждой вертикали. На любую из них, кроме тех, где маршрут начался и закончился, ладья должна была войти и после движения вдоль нее выйти. При этом вход и выход обязательно происходят с поворотами. Таким образом, общее число поворотов не меньше, чем 2(n–2)+1+1=2(n–1). Для любого n маршрут, содержащий ровно столько поворотов, можно получить из маршрута, приведенного на рис.20; при n=8 ладья делает 2(8–1)=14 поворотов.

Этот маршрут является открытым, замкнутый маршрут состоит уже из 16 ходов (рис.21).

Рис.20 Рис.

Вывод: задачи на нахождение числа фигур на шахматной доске и числа путей передвижения фигур более сложные, чем задачи на раскрашивание и разрезание доски. Для их решения нужны более сложные расчеты и умение найти математическую закономерность в найденном ряде чисел. Здесь уже большую помощь в решении задачи может оказать умение играть в шахматы.

3.4. Шахматы и геометрия

Обсуждая математические свойства доски, нельзя не упомянуть об одном старинном доказательстве на шахматной доске - доказательстве теоремы Пифагора. Разобьем доску на квадрат и четыре одинаковых прямоугольных треугольника (рис 22). На рис. 23 изображены те же четыре треугольника и два квадрата. Треугольники в обоих случаях занимают одну и ту же площадь, и следовательно ту же самую площадь занимают оставшиеся части без треугольников. Поскольку большой квадрат построен на гипотенузе прямоугольного треугольника, а маленькие на его катетах, то знаменитая теорема Пифагора доказана! Рис.22 и Рис.23.

20

4. Математические игры на шахматной доске

Необычные игры на шахматной доске придумывают не только шахматные композиторы-фантасты, но и математики. Правда, последние предпочитают игры, допускающие, математический анализ; изложенные в виде задач, они предлагаются на математических олимпиадах или включаются в различные сборники. В математических играх интерес представляет нахождение четкого алгоритма, гарантирующего победу или ничью. Но если алгоритм уже найден, то процесс игры теряет творческий характер, столь привлекающий нас в интеллектуальных играх.Любопытно, что в эпоху Возрождения была очень популярна специальная шахматно-математическая игра "арифметические шахматы", или, иначе, рифмомахия. На доске 16*8 передвигались три рода фигур - в форме круга, треугольника и прямоугольника. На каждой фигуре были написаны числа, комбинации которых определяли ходы, взятия и объявление мата. Игра требовала слишком сложных математических расчетов и постепенно была забыта.

4.1. Игра «Конь и верблюд»

В углу доски стоит конь, которым противники ходят по очереди. Первый игрок перемещает его как обычного коня, но с двойным ходом, а второй – как верблюда, то есть на три поля вдоль одной линии и на одно поле – вдоль другой. «Белые» начинают и стремятся поставить фигуру в противоположный угол, а «черные» стараются помешать им. Чем закончится игра?

Рис.24

В этом несколько странном соперничестве коня и верблюда (точнее было бы говорить о хамелеоне, превращающемся то в одну фигуру, то в другую) победителем выходит обычный конь. Если наша фигура стоит на большой диагонали, проходящей через исходное угловое поле, то на любое отступление верблюда с этой диагонали конь возвращается на нее, причем продвигается по крайней мере на одно поле ближе к цели. В конце концов он попадает в нужный угол.

4.2. Игра «Кошки-мышки»

У первого игрока всего одна фигура – мышка, а у другого несколько фигур – кошек. Мышка и кошки ходят одинаково – на одно поле по вертикали или горизонтали. Если мышка оказалась на краю доски, то очередным ходом она спрыгивает с нее и убегает от кошек; если кошка и мышка попадают на одно поле, то кошка съедает мышку.

Борьба кошек с мышкой протекает на обычной шахматной доске, причем играющие ходят по очереди и второй из них передвигает одним ходом сразу все свои кошки ( в любых направлениях). Начинает мышка, которая старается спрыгнуть с доски, а кошки хотят ее съесть.

Рис.25

4.3. Игра «Ферзя - в угол»

На доске стоит ферзь, которого два игрока по очереди передвигают на любое число полей либо вверх, либо вправо, либо вверх и вправо по диагонали ( то есть отступать ферзем нельзя).

Выигрывает тот, кто своим ходом загоняет ферзя в правый верхний угол доски – на поле h8.

Рис.26

4.4. Игра «Тур» коня

Эта игра «соло» коня по всей шахматной доске. Цель ее заключается в том, чтобы пройти конем через все 64 клетки, побывав на каждой только один раз. Существуют тысячи решений, т.к. конь может начинать движение с любой клетки.

Рис.27

5. Шахматы и компьютер

Уже сама легенда о создании шахмат, в которой мудрец запросил в качестве награды за изобретенную им игру сумму зерен пшеницы, расположенных на полях шахматной доски в геометрической прогрессии с шагом два, можно рассматривать как одно из начал информатики, ибо она аукается и в двоичную систему счисления, и в электронные таблицы. К этому стоит добавить, что в середине века шахматная доска служила вычислительным прибором арабским математикам.

Одна из задач человечества – успеть за отмеченным выше бурным развитием компьютерной техники, дабы не допустить превращение человечества в биологический придаток компьютера. Использование шахмат в качестве предметной области при изучении курса информатики способствует развитию человеческого интеллекта, помогая при этом понять преимущества и недостатки интеллекта компьютерного.

Рис.28

Научить компьютер играть в шахматы – одна из самых интересных задач в сфере искусственного интеллекта. Она была поставлена уже на заре вычислительной техники, в конце 50-х годов. В шахматах существуют определенные уровни мастерства, степени качества игры, которые могут дать четкие критерии интеллектуального роста машины. Поэтому компьютерными шахматами активно занимались ученные умы во всем мире. Но шахматы –игра, соревнование, и чтобы продемонстрировать свои логические способности, компьютеру необходим непосредственный противник. В 1974 году впервые прошел чемпионат мира по шахматам не между людьми, а между компьютерными программами. Победителем этого состязания стала советская шахматная программа «Каисса».

Вывод

В самом начале своей работы  мы поставили себе цель найти связь между шахматами и математикой, и считаю, что выполнил поставленную задачу. На примерах я подробно разобрал эту связь.

Итак, математика помогает шахматистам играть и выигрывать. А шахматы в свою очередь помогают нам решать как простейшие, так и самые сложные математические задачи, помогают ребятам развивать логику, внимание и таким образом знать математику на пять.

Гипотеза, выдвинутая мною: игра в «Шахматы» помогает при изучении математики, полностью подтвердилась. Я смог найти несколько тем в математике, связанных с игрой в шахматы.

Заключение

Подводя итог исследованию, можно наблюдать тесную связь между шахматами и математикой.

Шахматы - мощный стимул любознательности, который благотворно влияет на развитие памяти. Они помогают нам решать простейшие, и даже самые сложные математические задачи, развивать логику, внимание.

Для достижения своей цели шахматист должен научиться самостоятельно,  использовать имеющиеся у него знания и навыки для выбора решений применительно к разнообразным конкретным ситуациям. В этом процессе большое   значение приобретает овладение искусством сравнительного мыслительного анализа: умение находить различия в похожих ситуациях и сходство во внешне различных. Следовательно, можно сказать, что увлечение шахматами позволяет учащимся не только  на равных общаться с взрослыми, знакомиться с людьми разных профессий и возрастов, но и достигать определенных успехов в области математики так как в основе данной игры – логика, интуиция и нестандартное мышление.

В дальнейшем, я разберу то, что осталось для меня загадкой, и я обязательно буду продолжать играть в шахматы, чтобы знать математику на пять.

Список литературы:

1. Гарднер М. Математические чудеса и тайны. – М., Наука, 1978. – 127 с.

2. Гик Е. Я. Занимательные математические игры. – М., Знание, 1982. – 143 с.

3. Гик Е.Я. Шахматы и математика. - М., Наука, 1983. - 173 с.

4.Гусев В. А. Внеклассная работа по математике в 6-8 классах/ В. А. Гусев, А. И. Орлов, А. Л. Розенталь – М., Просвещение, 1984. – 164 с.

5. Гусев В.А. Математика – справочные материалы/ В.А. Гусев, А.Г. Мордкович – М., Просвещение, 1986. - 271с.

6.Игнатьев Е. И. В царстве смекалки. – М., Наука, 1984. – 189 с.

7. Лойд С. Математическая мозаика. – М., Мир, 1984. – 311 с.

8. Лангин В. Легенда о шахматном автомате. СПб., 1993.- 118 с.