Исследовательская работа по математике: "Шахматы в математике"

Городская конференция обучающихся бюджетных общеобразовательных учреждений «Шаги в науку»

Научное общество учащихся «Альфа» БОУ г. Омска «СОШ»№151»

Образовательная область «Математика»

Шахматы в математике

Штумпф Дмитрий Юрьевич,

6-2 класс, БОУ г. Омска

«СОШ №151»

Научный руководитель:

Спицына Татьяна Петровна,

учитель математики,

БОУ г. Омска «СОШ№151»

Омск, 2013г.

Оглавление

Стр.

Введение.----------------------------------------------------------------------------- 3

Глава 1.Шахматы и математика------. -------------------------------------------5

1.1. Происхождение шахмат. ------------------------------------------------------5

1.2. Правила игры в шахматы-----------------------------------------------------7

1.3. Математические задачи на шахматной доске-----------------------------8

1.4. Головоломки на шахматной доске. -----------------------------------------13

2. Шахматные задачи в книгах по математике-------------------------------18

2.1. Шахматные задачи на олимпиадах-----------------------------------------18

2.2 Шахматные задачи в занимательных книгах-----------------------------20

2.3. Шахматные задачи в учебниках--------------------------------------------23

3. Заключение. -----------------------------------------------------------------------24

Список литературы. ----------------------------------------------------------------25

Введение

Известный педагог В. Сухомлинский писал: «… без шахмат нельзя себе представить воспитание умственных способностей и памяти».

Игра в шахматы развивает умственные способности ребенка, фантазию, тренирует его память, формирует и совершенствует такие качества, как: воля к победе, решительность, стойкость, выносливость, выдержка, терпение, находчивость, сосредоточенность, дисциплинированность мысли.

Актуальность исследования. У шахмат и математики много родственного. Выдающийся математик Г. Харди, проводя параллель между этими двумя видами человеческой деятельности, в своей статье «Исповедь математика» заметил, что решение проблем шахматной игры есть не что иное, как математическое упражнение, а игра в шахматы это как бы насвистывание математических мелодий. Шахматная доска, фигуры и сама игра часто пользуются для иллюстрации разнообразных математических понятий и задач. Шахматные примеры и термины можно встретить в литературе по кибернетике, теории игр, вычислительной математике, исследованию операций, теории графов, теории чисел и комбинаторике. Важное место занимают шахматы в развитии современных методов программирования на электронных вычислительных машинах. Ещё одна точка соприкосновения математики и шахмат – это один из популярных жанров занимательной математики, к которому относятся математические игры, задачи и развлечения на шахматной доске. Почти в каждом сборнике олимпиадных задач по математике или книгах головоломок и математических досугов можно встретить красивые и остроумные задачи с участием шахматной доски и фигур. Многие из них имеют интересную историю и привлекли к себе внимание известных учёных. Например, задачей о ходе коня занимался великий математик Леонард Эйлер, а задачей о восьми ферзях – другой великий математик Карл Гаусс (рис. 1).

Рис. 1. Восемь ферзей

Цель исследования – рассмотреть применение задач, связанных с шахматной доской и шахматными фигурами в математике.

Задачи исследования:

1. изучение учебной, справочной, занимательной литературы и интернет - источников;

2. выбор задач, связанных с шахматной доской и шахматными фигурами из литературы;

3. выделение видов шахматных задач в математике.

Методы исследования: анализ учебной, справочной, занимательной литературы и интернет-источников; анализ видов, применяемых шахматных задач.

Объект исследования – шахматы и математика.

Предмет исследования – задачи по математике с применением шахматной доски и шахматных фигур.

Гипотеза исследования: рассмотрев применение задач, связанных с шахматной доской и шахматными фигурами в математике, мы убедимся, что у математики и шахмат много родственного.

Структура работы: работа состоит из введения, двух глав, каждая из которых состоит из , заключения, списка литературы

Глава 1. Шахматы и математика

1. О появлении шахмат

О том, что шахматы впервые появились в Индии, известно всем. А вот все ли знают, как долго и через какие этапы шли шахматы к современному виду. Сначала появилась так называемая чатуранга (четырехсоставное войско), где игра сводилась не к матованию короля, а к уничтожению всех сил каждого из соперников, которые делали ходы поочередно, в зависимости от показаний игральной кости. Так, если выпадала цифра 2, то играла ладья, 3 –конь, 4 – слон и так далее. Чатуранга возникла в Северной Индии не позже 5 века. На рубеже VI – VII веков чатуранга превратилась в шатрандж (или в шатранг) – игру для двух соперников, внешне схожую с нынешними шахматами, но с иными правилами. Здесь не было рокировки, пешка передвигалась лишь на одно поле и превращалась только в ферзя. Сам ферзь считался слабой фигурой и ходил так же, как и в современных шахматах. Выигрышем считался не только мат, но и пат. Кроме того, победителем считался тот, кто забирал все фигуры соперника, даже если у сильнейшей стороны к этому моменту оставалась только одна фигура или пешка.

Раз уж речь зашла о происхождении шахмат, то уместно привести одну гипотезу, использующую некоторые математические свойства доски. Согласно этой гипотезе шахматы произошли из так называемых магических квадратов.

Магический квадрат порядка n представляет собой квадратную таблицу nґn, заполненную целыми числами от 1 до n² и обладающую следующим свойством: сумма чисел каждой строки, каждого столбца, а также двух главных диагоналей одна и та же. Для магических квадратов порядка 8 она равна 260 (рис. 2).

Рис. 2. Альмуджаннах и магический квадрат.

Закономерность расположения чисел в магических квадратах придает им волшебную силу искусства. Недаром выдающийся немецкий художник А. Дюрер был настолько очарован этими математическими объектами, что воспроизвел магический квадрат в своей знаменитой гравюре “Меланхолия”.

Рассмотрим одну из старинных дебютных табий (начальных расположений фигур) под названием альмуджаннах. Она получается из современной расстановки при помощи следующих симметричных ходов белых и черных: 1. d3 d6 2. e3 e6 3. b3 b6 4. g3 g6 5. c3 c6 6. f3 f6 7. c4 c5 8. f4 f5 9. Кc3 Кc6 10. Кf3 Кf6 11. Лb1 Лb8 12. Лg1 Лg8 (рис. 1).

Подсчитав сумму чисел, стоящих на восьми полях — d2, d3, e2, e3, d6, d7, e6, e7, участвующих в первые двух ходах, мы неожиданно получим магическое числе 260. Тот же результат даст и каждая последующая пара приведенных ходов. Подобные примеры (число их можно увеличить) и позволяют высказать гипотезу о связи магических квадратов с шахматами. А исчезновение всех следов этой связи можно объяснить тем, что в далекую эпоху суеверий и мистики древние индусы и арабы приписывали числовым сочетаниям магических квадратов таинственные свойства, и эти квадраты тщательно скрывались. Может быть, поэтому и была выдумана легенда о мудреце, который изобрел шахматы.

1. Правила игры в шахматы

В шахматах на сегодняшний день сложились очень сложные правила игры. Главные фигуры расставляются от а1 до h1,а пешки от а2 до h2. При этом фигуры, кроме пешек, имеют свои возможности передвижения. Пешки могут передвигаться только на одну клетку, но при первом ходе пешкой можно походить через одну клетку и всегда только вперед. Рубят они только по диагонали. Ладья, не имея ограничений, может передвигаться на любое расстояние по горизонтали и вертикали. Конь ходит буквой Г, делая ход через препятствующие фигуры. Слон ходит по диагонали на любое расстояние. Ферзь в принципе не имеет ограничений, и может ходить как по горизонтали и вертикали, так и по диагонали на любое количество клеток. Король также может передвигаться в любом направлении, но только на одну клетку. Вся игра сводиться к матованию короля. Кроме того, существует масса нюансов, связанных с рокировкой в короткую или длинную сторону. Дойдя до противоположной стороны игрового поля, пешка может стать любой другой фигурой (естественно кроме короля), в том числе и ферзем, который представляет значительную силу в «шахматном сражении». В настоящее время разработаны различные пособия, книги, в которых описываются разнообразные возникающие ситуации и возможности выхода из них. В 1912 году в Риме на итальянском языке вышло руководство португальца Дамиано под названием «Книга учит играть в шахматы и содержит задачи». Вот несколько советов Дамиано: «никакой ход не должен быть сделан без цели», «не должно играть скоро», «когда имеешь в виду хороший ход, то все – таки посмотри, нет ли еще лучшего».

1. Математические задачи на шахматной доске

зерен. Это число записывается двадцатью цифрами и является фантастически большим. Подсчет показывает, что амбар для хранения необходимого зерна с площадью основания 80 м² должен простираться от Земли до Солнца. [Живая математика]. Конечно, связь с математикой здесь несколько условна, однако неожиданная развязка истории наглядно иллюстрирует грандиозные математические возможности, скрывающиеся в шахматной игре.

Среди математических задач и головоломок о шахматной доске наиболее популярны задачи на разрезание доски. Первая из них также связана с легендой об алмазах.

З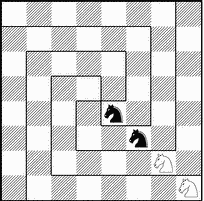адача 2. Один восточный властелин был таким искусным игроком, что за всю жизнь потерпел всего четыре поражения. В честь своих победителей, четырех мудрецов, он приказал вставить в его шахматную доску четыре алмаза — на те поля, на которых был заматован его король (см. рис. 3, где вместо алмазов изображены кони). После смерти властелина его сын, слабый игрок и жестокий деспот, решил отомстить мудрецам, обыгравшим его отца. Он велел разделить им шахматную доску с алмазами на четыре одинаковые по форме части так, чтобы каждая заключала в себе по одному алмазу. Хотя мудрецы выполнили требование нового властелина, он все равно лишил их жизни, причем, как гласит легенда, для казни каждого мудреца использовал его часть доски с алмазом. Эта задача о разрезании доски часто встречается в занимательной литературе.

Рис.3. Разрезание на 4 равные части

Разрезать доску на четыре одинаковые части (совпадающие при наложении) так, чтобы на каждой из них оказалось по одному коню. Предполагается, что разрезы проходят только по границам между вертикалями и горизонталями доски. Одно из решений задачи представлено на рис. 2. Располагая четырех коней на различных полях доски, мы получаем множество задач о разрезании. Интерес в них представляет не только нахождение одного необходимого разреза, но и подсчет числа всех способов разрезать доску на четыре одинаковые части, содержащие по одному коню. Установлено, что наибольшее число решений — 800 — задача имеет при расположении коней в углах доски.

Следующую задачу на разрезание обычно связывают с именем выдающегося шахматного композитора и мастера головоломок С. Лойда.

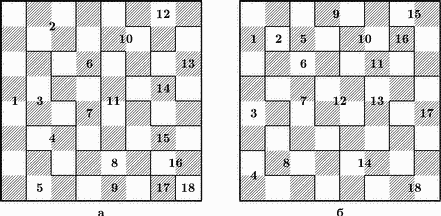
Рис. 4. Задача о разрезании доски.

Задача 3. На какое максимальное число частей можно разрезать шахматную доску, если считать разными части, отличающиеся своей формой или цветом полей при совмещении. Переворачивать части не разрешается (а поворачивать можно).

Максимальное число частей равно 18. На рис. 4 представлены два способа. Решение на рис. 4,а принадлежит Лойду; особенность его состоит в том, что одна из частей содержит восемь полей (максимум). В решении на рис. 4,б, отличающемся внешней симметрией, ни одна часть не содержит более пяти полей. На рис. 3,а части 17 и 18, или 8 и 9, хотя и имеют одинаковую форму, отличаются цветом полей при совмещении. Другие части, например, 3 и 6, вообще не могут быть совмещены (переворачивать их нельзя).

Задача 4. В двух следующих задачах требуется разрезать шахматную доску на самые мелкие части, т.е. на отдельные поля.

Пусть разрезанные части доски разрешается прикладывать друг к другу так, чтобы следующий разрез мог рассечь не одну, а несколько частей. Сколько разрезов надо произвести, чтобы получить 64 отдельных поля доски?

Сначала разрежем доску пополам. Затем положим обе половины рядом и проведем второй разрез, получая четыре одинаковые части и т.д. Так как каждый разрез увеличивает число частей вдвое, то после шестого разреза доска распадается на 64 поля (64=2⁶).

Задача 5. Пусть теперь каждую часть доски разрешается разрезать только в отдельности. Сколько разрезов понадобится в этом случае, чтобы получить 64 отдельных поля?

Обычно эта задача, особенно если она предлагается сразу после предыдущей, вызывает определенные трудности. Вероятно, у решающих задачу в какой-то мере проявляется инерционность мышления. Ведь сразу видно, что придется произвести 63 разреза. Действительно, каждый разрез увеличивает число частей на единицу, но перед тем, как произвести первый разрез, мы имели одну часть (саму доску), а в результате их должно стать 64 (все поля доски).

До сих пор мы считали, что разрезы обязательно проходят между вертикалями и горизонталями доски, т.е. ровно по границам полей. В следующих двух задачах это условие не принимается во внимание.

Задача 6. Какое максимальное число полей доски можно пересечь одним разрезом?

Произвести разрез доски — это то же самое, что провести на ней прямую. Другими словами, нам нужно определить максимальное число полей, которое может пересечь прямая, проведенная на доске. Поля доски образуются в результате пересечения 18 прямых — девяти вертикальных и девяти горизонтальных. С каждой из них прямая-разрез может пересечься лишь в одной точке, но из четырех прямых, образующих края доски, она пересекается лишьс двумя. Отсюда следует, что наша прямая пересекает прямые, образующие поля доски, самое большее в 16 точках. Эти точки разбивают прямую не более чем на 15 отрезков, каждый из которых заключен внутри какого-нибудь поля. Таким образом, любой разрез доски пересекает не более 15 полей. Из рис. 5 следует, что ровно столько полей пересекает разрез, проведенный параллельно диагонали доски и проходящий через середины сторон двух угловых клеток.

Рис. 5. Пятнадцать полей пересечены одной прямой.

Итак, одним разрезом можно пересечь 15 полей доски. Естественно, возникает следующая задача.

Задача 7. Сколько нужно провести разрезов (прямых) на доске, чтобы пересечь все ее поля?

Разумеется, восьми разрезов вполне достаточно — по одному вдоль каждой вертикали или каждой горизонтали. Однако, оказывается, что и семь прямых могут пересечь все 64 поля доски. Для этого одну прямую нужно провести почти в диагональном направлении через центр доски, а шесть других — в направлениях почти параллельных второй диагонали доски (рис. 6).

Рис. 6. Семь прямых пересекают все поля доски.

1. Головоломки на шахматной доске

Первоначально поля шахматной доски не были раскрашены поочередно в черный и белый (или какие-либо два других) цвета, и это усовершенствование было введено, просто чтобы помочь глазу при игре. Польза такой раскраски несомненна. Например, она облегчает манипуляции со слонами, позволяя с одного взгляда оценить, что наш король или пешки на черных клетках не находятся под угрозой вражеского слона, передвигающая по белым клеткам. И все же раскраска шахматной доски не существенна для самой игры как таковой. Точно так же, когда мы формируем головоломки на шахматной доске, часто неплохо помнить, что дополнительный интерес может представлять «обобщение» на случай доски с любым числом клеток или ограничение задачи некой конфигурацией клеток, не обязательно квадратной. Ниже приведены несколько головоломок такого типа.

Рассмотрим несколько знаменитых головоломок на шахматной доске, которые носят математический характер.

Задача 1. Парадокс шахматной доски.

Проделаем мысленно некоторые ма­нипуляции с шахматной доской. Разрежем ее на четыре части, как показано на рисунке 1 (по­ля специально не раскрашены), и составим из них прямоугольник (рис.2).

Шахматная доска состоит из 64 клеток, а вот полученный прямоугольник — из 65. При разрезании доски откуда-то взялось одно лиш­нее поле!

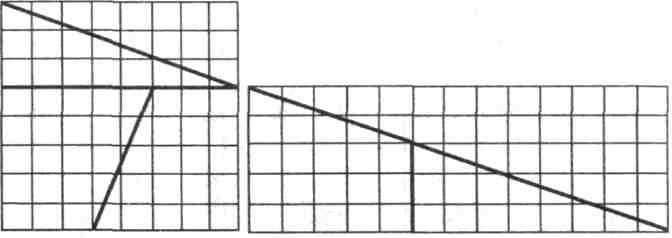
Рис 8

Р

Рис 1

З

Рис 4

Можно ли покрыть костями домино 2x1 ква­драт 8x8, из которого вырезаны противополож­ные угловые клетки? (рис. 9).

М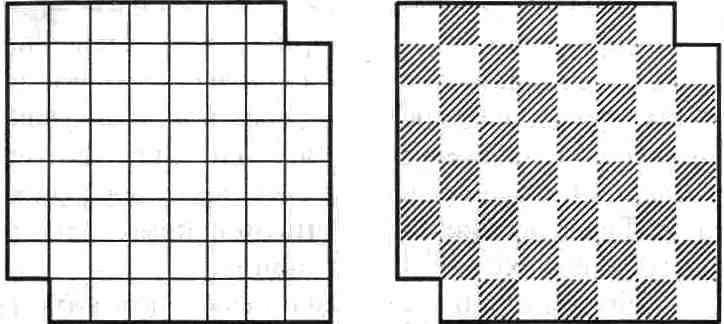

Рис 9

При покрытии доски каждая кость домино занимает одно белое и одно черное поле, и, зна­чит, весь набор костей (в количестве 31 штуки) покрывает одинаковое число белых и черных по­лей. Но на нашей урезанной доске черных полей на два меньше, чем белых (вырезанные поля чер­ные), и, следовательно, необходимого покрытия не существует! Итак, раскраска доски не только помогает шахматисту ориентироваться во время игры, но и позволяет решать необычные математические головоломки.

В рассмотренной задаче существенным было не то, что удалены угловые поля доски, а то, что они одного цвета. Из наших рассуждений следует, что какую бы пару одноцветных полей ни вырезать, покрыть домино оставшуюся часть доски не удастся. Возникает такая задача.

Задача 3. Пусть на шахматной доске вырезаны два поля разного цвета. Всегда ли можно покрыть оставшуюся часть доски 31 домино?

Оказывается, что всегда. Проведем замкнутую линию, как показано на рис. 11. Если из доски вырезаны соседние поля, то разорванная линия будет состоять из одного куска, проходящего через 62 поля, при этом цвета полей чередуются. Если мы станем размещать домино вдоль этой линии, то закроем всю оставшуюся часть доски. Если вырезанные поля не являются соседними, то линия разорвется на две части, проходящие через четное число полей, и каждую из них можно покрыть домино.

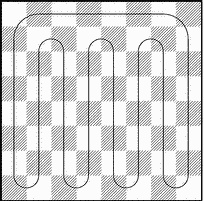
Рис. 11. Домино покрывают доску

Задача 4. Пусть из шахматной доски вырезано некоторое количество полей. При каком наименьшем числе таких полей на оставшуюся часть доски нельзя поместить ни одного домино?

Достаточно вырезать из доски 32 поля одного цвета — либо белые, либо черные, и на ней не останется места ни для одного домино.

Задача 5. Можно ли доску покрыть домино так, чтобы на ней нельзя было провести ни одной границы между вертикалями или горизонталями, не пересекая домино?

Если представить себе, что доска — это стенка, а домино — кирпичи, то существование указанной границы (шва) свидетельствует о непрочной кладке. Иначе говоря, в задаче спрашивается, можно ли расположить “кирпичи” так, чтобы “стенка” не рухнула. Прямоугольник, который удается покрыть необходимым образом, называется прочным. Построение, приведенное на рис. 12, показывает, что шахматная доска является прочной. В общем случае, из домино можно сложить произвольный прочный прямоугольник, площадь которого четна, а длина и ширина больше четырех; исключение составляет лишь квадрат 6*6.

Рис. 12. Прочная шахматная доска

Задачи о шахматных досках и домино составляют лишь небольшую часть целой серии задач такого сорта. В общем случае вместо домино рассматриваются так называемые полимино, представляющее собой односвязную фигуру, состоящую из квадратов. С точки зрения шахматиста, односвязность означает, что все квадраты полимино можно обойти ходом ладьи. В зависимости от числа квадратов, полимино бывают различного типа. Мономино содержит один квадрат, домино — два, тримино — три, тетрамино — четыре, пентамино — пять и т.д. (полимино, содержащие более двух квадратов, имеют различную форму). В задачах о полимино покрываются разнообразные доски, не обязательно прямоугольные.

Остановимся еще на нескольких вопросах, связанных с покрытием обычной шахматной доски. Очевидно, покрыть ее только прямыми тримино, т.е. домино 3*1, невозможно, так как 64 не делится на 3. Возникает следующая задача.

Задача 6. Можно ли покрыть шахматную доску 21 прямым тримино и одним мономино? Если можно, то какие поля занимает при этом мономино?

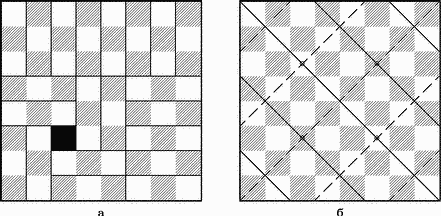
^{Рис. 13. Задача о тримино.}

Одно из покрытий показано на рис. 13,а. Для определения возможных расположений мономино проведем на доске две системы параллельных прямых, как показано на рис. 13,б. Легко убедиться, что при любом покрытии доски каждое тримино покрывает ровно одно поле, через которое проходит сплошная прямая, и ровно одно, через которое проходит пунктирная прямая Поскольку число полей, пересекаемых сплошными прямыми, равно 22, как и число полей, пересекаемых пунктирными прямыми, а тримино имеется 21, то мономино может занимать лишь поля, пересекаемые обоими семействами прямых. А таких полей всего четыре: c3, c6, f3 и f6. Поворачивая доску на 90, 180 и 270⁰, можно получить соответствующее покрытие для каждого из этих четырех полей.

Глава 2. Шахматные задачи в книгах по математике

Шахматные задачи можно встретить в различных книгах.

2.1. Шахматные задачи на олимпиадах [2]

1. 1946 год. В шахматном турнире участвовали два ученика 7 класса и некоторое число учеников 8 класса. Два семиклассника набрали вместе восемь очков, а все восьмиклассники набрали по одинаковому числу очков. Сколько восьмиклассников участвовали в турнире? (7 или14).

2. 1946 год. В шахматном турнире участвовали ученики 9 и 10 классов. Десятиклассников было в десять раз больше, чем девятиклассников, и они набрали вместе в 4,5 раза больше очков, чем девятиклассники. Сколько очков набрали девятиклассники? (10).

3. 1946 год. Сколько различных по величине или по расположению квадратов, состоящих из целого числа клеток, можно начертить на шахматной доске в 64 клетки? (1² +2² +…+8² =204).

4. 1955 год. В турнире собираются принять участие 25 шахматистов. Все они играют в разную силу, и при встрече всегда побеждает сильнейший. Какое наименьшее число партий требуется, чтобы определить двух сильнейших игроков? (28 партий. Сначала по олимпийской системе за 25-1=24 партии определяется чемпион. Второй по силе – тот, с кем играл чемпион; их может быть 5. По олимпийской системе ещё за 4 партии выявляем чемпиона среди них).

5. 1959 год. Доказать, что шахматную доску размером 4*4 нельзя обойти ходом шахматного коня, побывав на каждом поле ровно один раз.

6. 1961 год. На шахматной доске выбраны две клетки одинакового цвета. Доказать, что ладья, начав с первой из этих клеток, может обойти все клетки по разу, а на второй выбранной клетке побывать два раза.

7. 1967 год. На шахматной доске размером 1000*1000 находятся черный король и 499 белых ладей. Черные и белые фигуры ходят по очереди. Доказать, что как бы не ходила ладья, король всегда может за несколько ходов встать под бой одной из них. (Если предположить, что король не разу не встал под шах, то каждая ладья должна была по ходу игры сменить как свою первоначальную вертикаль. Так и свою первоначальную горизонталь, т. е. сделать не менее двух ходов. Отсюда общее число ходов всех ладей не меньше 20. Но это число должно совпадать с числом ходов короля, т. е. быть равным 19. Противоречие.)

8. 1969 год. Белая ладья преследует черного слона на доске 3*1969 клеток (они ходят по очереди по обычным правилам). Как должна играть ладья, чтобы взять слона? Первый ход делают белые. (Ладья должна двигаться по средней линии доски. Отставая от слона на ход коня.)

9. 1969 год. На шахматной доске на поле а1 стоит белый конь. Двое по очереди замазывают по одной клетке шахматной доски бокситовым клеем. При этом они должны замазывать так, чтобы конь мог пройти в любую незамазанную клетку, нигде не приклеевшись (конь ходит по обычным шахматным правилам). Проигрывает тот, кто не может сделать очередного хода. Кто выигрываетпри правильной игре: сделавший первый ход или его партнер? (Как бы не играли партнеры, тот, за кем очередь, всегда сможет сделать свой ход, если есть еще хоть одна незамазанная клетка. Поскольку всего клеток на доске 63 ( не считая клетки а1), выигрывает независимо от хода игры начинающий.)

10. 1975 год. На шахматной доске 8*8 отмечены 64 точки – центры всех клеток. Можно ли отделить все точки друг от друга, проведя 13 прямых, не проходящих через эти точки? (Нельзя. Для доказательства соединим центры 28 крайних клеток доски. Получим замкнутый контур квадрата Г. Каждая из 13-ти прямых пересекает контур Г не более чем в двух точках, откуда общее число точек пересечения с Г не более чем в двух точках, откуда общее число точек пересечения с Г не больше 26, а они не могут отделить друг от друга даже эти 28 центров, а тем более все центры.)

11. 1984 год. На шахматной доске 20*20 стоят 10 ладей и один король. Король не стоит под шахом и идет из левого угла в правый верхний по диагонали. Ходят по очереди: сначала король, потом одна из ладей. Доказать, что при любом начальном расположении ладей и любом способе маневрирования ими король попадет под шах. (Если предположить, что король не разу не встал под шах, то каждая ладья должна была по ходу игры сменить как свою первоначальную вертикаль. Так и свою первоначальную горизонталь, т. е. сделать не менее двух ходов. Отсюда общее число ходов всех ладей не меньше 20. Но это число должно совпадать с числом ходов короля, т. е. быть равным 19. Противоречие.)

2.2. Шахматные задачи в книгах по занимательной математике

1. Конь на доске 3*3. [6]

На части шахматной доске размером 3х3 в одной из клеток стоит конь. Можно ли им обойти все девять клеток этой части доски.

1. Конь и шестнадцать пешек.

На шахматной доске расставлены 16 пешек.

На какую свободную клетку доски надо поставить шахматного коня, чтобы им можно было снять с доски все пешки, сделав при этом наименьшее возможное число ходов?

1. Четыре коня.

На шахматной доске стоят 4 коня. Требуется разделить доску на 4 одинаковые по форме части, на каждой из которых стол бы в точности один конь.

1. Пешка и конь.

Поставим на шахматную доску одну пешку. Может ли конь, помещенный на одну из свободных клеток, обойти все остальные свободные клетки и вернуться на исходную, побывав на каждом поле только один раз.

1. Две пешки и конь.

Поставим две пешки в противоположные углы шахматной доски. Может ли конь обойти оставшуюся часть доски так, как это требуется в предыдущей задаче.

1. Конь.

Может ли конь обойти 16 центральных полей шахматной доски, побывав на каждом поле по одному разу?

1. Жуки

Представьте что вам удалось поймать 25 жуков и расставить их по одному на каждой клетке шахматной доски размером 5х5 (см. рисунок).

Давайте предположим теперь, что каждый жук переполз на соседнюю по горизонтали или вертикали клетку этой части доски. Как вы думаете, останутся ли при этом пустые клетки.

1. Жук на шахматной доске.

Каков будет ответ на вопрос предыдущей задачи для всей шахматной доски размером 8х8.

1. Замкнутый путь жука.

Может ли жук, помещенный на некоторую клетку шахматной доски, переползая на соседние клетки по горизонтали или вертикали, обойти всю доску и вернуться на исходную клетку, побывав при этом на каждой клетке только один раз?

1. Пешка и домино.

Предположим, что у нас имеется шахматная доска и 32 косточки домино, каждая величиной в две клетки доски. Поставим на какую-нибудь клетку доску пешку. Можно ли оставшуюся часть доски покрыть косточками домино так, чтобы ни одна косточка не вылезала за пределы доски и косточки не налегали друг на друга?

1. Две пешки и домино.

Поставим две пешки на противоположные углы поля доски. Можно ли оставшуюся часть доски покрыть косточками домино так, как это требовалось в предыдущей задаче?

1. Опять две пешка и домино.

Поставим две пешки на поля разного цвета. Можно ли оставшуюся часть доски покрыть косточками домино?

1. Шахматные фигуры и домино.

Сколько шахматных фигур нужно поставить на доску для того чтобы на ней нельзя было разместить ни одной косточки домино.

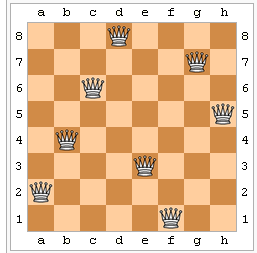
1. О восьми ферзях.

На шахматной доске, состоящей из шестидесяти четырех клеток, расставьте 8 ферзей так, чтобы ни один из них не мог бить другого. Иными словами: на восьми клетках шахматной доски поставить 8 ферзей так, чтобы каждые два из них не были расположены ни на одной линии, параллельной какому-либо краю, и на одной из прямых, параллельных какой-нибудь диагонали доски.

1. О ходе шахматного коня.

Мы встречались уже с вопросом, может ли конь обойти часть шахматной доски, побывав при этом на каждом поле только один раз. Решение.

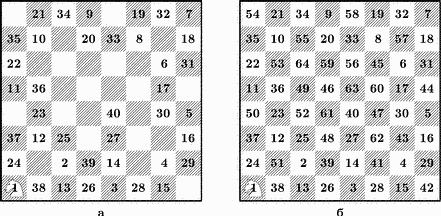
Вот еще одна старинная задача о ходе шахматного коня. Требуется обойти конем все 64 клетки шахматной доски так, чтобы на каждой клетке конь был только один раз и затем возвратился бы в клетку, из которой вышел.

2.3. Шахматные задачи в учебниках по математике

№ 1284 [1]. Шахматная доска состоит из 8 рядов, по 8 клеток в каждом из них. Какую часть доски составляет: а) один ряд клеток; б) 3 ряда клеток; в) одна клетка; г) 7 клеток?

Шахматный конь может двигаться на две клетки по вертикали и на одну клетку в сторону. Подумайте , может ли конь переместиться из клетки А (поле а8) шахматной доски в клетку В (н1).

Решение. а) 8/64=1/8; б) 24/64=3/8; в) 1/64; г) 7/64.

Заключение

Почти в каждом сборнике олимпиадных задач по математике или книгах головоломок и математических досугов можно встретить красивые и остроумные задачи с участием шахматной доски и фигур. Многие из них имеют интересную историю и привлекли к себе внимание известных учёных. Например, задачей о ходе коня занимался великий математик Леонард Эйлер, а задачей о восьми ферзях – другой великий математик Карл Гаусс.

Цель исследования – рассмотреть применение задач, связанных с шахматной доской и шахматными фигурами в математике нами достигнута.

Можно выделить такие виды шахматных задач в математике:

• на расстановку шахматных фигур;

• о ходах шахматных фигур

• на разрезание шахматной доски;

• с участием домино (тримино);

• о количестве участников (теория турниров. комбинаторика).

В шахматах легко сформулировать конечную и многие промежуточные цели, практически невозможно дать точного рецепта для их достижения. Выбор хода в шахматной партии – это и есть принятие решения с учетом обстановки и способностью сопоставлять и оценивать различные ситуации, делая различные выводы. Безусловно, шахматы и математика напрямую связаны между собой. Обдумывая очередной свой ход, шахматист, а так же математик, решающий задачу, заставляет свой мозг проделывать колоссальную работу. Здесь и цепочки логических рассуждений, и скрытая от мысленного взора работа подсознания, и обращение к кладовым памяти, оживляющее зрительные ассоциации и питающие интуицию. Множество математических приемов позволяют облегчить рассуждения для шахматиста.

Список литературы

1. Учебник – Математика. 5 класс: Виленкин Н. Я. и др., Москва: Мнемозина, 2008 г.

2. Гальперин Г.А., Толпыго А.К. Московские математические олимпиады: Кн. для учащихся / Под. Ред. А. Н. Колмогорова. – М.: Просвещение, 1986. – 303 с., ил. (олимпиады с 1935 года по 1985 год для 7-10 классов).

3. Гик Е.А. Шахматы и математика. М.: Наука. Главная редакция физико-математической литературы, 1983 г., 177 с. –( Библиотечка «Квант», вып. 24)

4. Губницкий С. Б. Шедей С.А. Полный курс шахмат. 64 рока для новичков и не очень опытных игроков.- Харьков.: Фолио; М.; ООО фирма «Издательство АСТ», 1999 г.-544 с.

5. Журавлев Н.И. Шаг за шагом. (Предисл. М.Таха)- М., Физкультура и спорт, 1986 г. -288 с.

6. Игнатьев Е.И. В царстве смекалки. – м.:АО «Столетие», 1994 г.192 с.

7. Нестеренко Ю.В., Олехник С. Н., Потапов М. К. Лучшие задачи на смекалку. – М.: Научно-технический центр «Университетский»: АСТ-ПРЕСС, 1999. – 304 с.: ил.

8. Перельман Я.И. Живая математика. Математические рассказы и головоломки. (Серия «Занимательная наука), 1994 г.

9. http://chess

10. http://www.bs-chess.com

11. http://suvenir-2003.narod.ru/prod02.htm

12. http://www.pc.com.ua/art/rus/galery

25