Россия, Арзамас
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 18.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 07.11.2024 21:24
Агафонова Наталья Васильевна
Учитель математики
58 лет
1 554
39 292 
Местоположение
Специализация
Исследовательская работа "Флексагон"
Категория:
Математика
24.02.2018 14:44
Просмотр содержимого документа
«Исследовательская работа "Флексагон"»
муниципальное бюджетное общеобразовательное учреждение
«Средняя школа № 15»
Выполнил:
ученик 6 «Б» класса
Сорокин Максим
Руководитель:
учитель математики
Агафонова Наталья Васильевна
г. Арзамас 2017 год
Оглавление.
Введение…………………………………………………………………………3
Глава I. …………………………………………………………………………..5
1. История возникновения флексагонов………………………………………………………………..…….5
2. Виды флексагонов………………………………………………..…………… 6
3. Плоские сгибаемые многоугольники…………………………………….…………………………..…7
а) Тетрафлексагоны………………………………………………………………...8
б) Гексафлексагоны…………………………………………………………….….8
4. Объёмные сгибаемые многогранники………………………………….…..…8
а) Кольцевые флексагоны……………………………………………………..….9
б) Объёмный тетрафлексагон…………………………………………………….9
в) Флексотрубка……………………………………………………………….....10
Глава II…………………………………………………………………….…..….10
1. Исследование флексагонов………………………………………………..….11
2. Применение флексагонов…………………………………………………..…………………..13
Заключение……………………………………………………………………….16
Список литературы. ……………………………………………………………..17
Приложения.
Введение
Есть в математике нечто, вызывающее человеческий восторг.
Ф. Хаусдорф.
Занимательную математику любят все. Элемент игры, который делает её интересной, может быть представлен в виде головоломки, ребуса, шарады, фокуса, парадокса. Решая нестандартные математические задачи, человек испытывает радость приобщения к творческому мышлению, интуитивно ощущает красоту и величие математики. Нестандартные задачи развивают наблюдательность, умение логически мыслить, пробуждают веру в свои силы.
Математика – предмет очень важный и очень сложный. Большинство школьников испытывает затруднения при его изучении. Многие ребята считают этот предмет скучным и неинтересным.
Актуальность. Знакомство с флексагонами позволит по-новому взглянуть на мир математики и внести разнообразие в привычные окружающие нас предметы быта и интерьера, а также способствует развитию пространственного воображения.
Испытывая большой интерес к занимательной математике, я захотел познакомиться с загадочными, увлекательными и имеющими практическое применение математическими объектами, которые не рассматриваются в школьном курсе. На математических интернет-сайтах мое внимание привлекли флексагоны и флексоры, им я и решил посвятить свою исследовательскую работу.
Флексагоны способствуют развитию пространственного воображения и имеют практическое применение. Сначала может показаться, что это всего лишь игрушки, но они таят в себе много загадок.
Что же это такое флексагон? Какие тайны связаны с ним? Как его построить? Где взять чертёж?
Таким образом, объектом моего исследования являются флексагоны, а предметом - история их возникновения, способы конструирования, применение.
Гипотеза. Флексагоны – это не просто игрушка или обычное оригами, а занимательная математическая головоломка.
Так появилась цель работы: изучить мир флексагонов.
Задачи исследования:
познакомиться со специальной литературой, раскрыть содержание понятия «флексагон», «флексор»;
найти информацию по построению флексагонов и флексоров;
создать модели простейших флексагонов, флексоров;
выявить области применения флексагонов в жизни человека;
пробудить интерес одноклассников к математике, продемонстрировав на примере данной работы, что эта точная наука математика удивительна, необычна и занимательна.
Методы исследования: сбор информации, анализ литературы, классификация, наблюдение, сравнение, создание наглядных моделей и обобщение материала.
Глава I
1. История возникновения флексагонов.
Как и многие удивительные вещи в мире, флексагоны были открыты случайно. Придумать флексагоны помогло одно обстоятельство: различие в формате английских и американских блокнотов. Американский лист короче привычного международного формата А4 на 18 мм. Если бы не эта разница, возможно, мы бы до сих пор не знали о флексагонах — увлекательной игрушке, головоломке и интересной математической модели, открытой в первой половине XX века.
В конце 1939 года Артур Х. Стоун, двадцатитрёхлетний аспирант из Англии, изучавший математику в Принстонском университете (США), обрезая листы американского блокнота, решил немного развлечься.
Артур Х. Стоун Принстонский университет, штат Нью-Джерси
Он складывал из отрезанных полосок бумаги разные фигуры. Одна из сделанных им фигур оказалась особенно интересной. Перегнув полоску бумаги в трёх местах и соединив концы, он получил правильный шестиугольник. Взяв этот шестиугольник за два смежных треугольника, Стоун подогнул противоположный угол вниз так, что его вершина совпала с центром фигуры. При этом Стоун обратил внимание на то, что, когда шестиугольник раскрывался, как бутон, видимой становилась совсем другая поверхность.
Если бы обе стороны исходного шестиугольника были разного цвета, то после перегибания видимая поверхность изменила бы свою окраску. Так был открыт самый первый флексагон с тремя поверхностями. Впоследствии оказалось, что можно построить и более сложный шестиугольник с шестью поверхностями вместо трёх. Почувствовав, что за загадочной фигурой скрывается интересная математическая теория, Стоун поделился своим открытием с друзьями. Друзья – физик Ричард Фейнман, математики Брайан Таккерман и Джон Тьюки – назвали изобретенную Стоуном фигуру флексагоном (от английского to flex – «складываться, сгибаться, гнуться»). В шутку они назвали себя «Флексагонным комитетом» и принялись за изучение математических основ науки «флексологии».
Так что же это такое флексагон?!
Флексагоны – это многоугольники, сложенные из полосок бумаги прямоугольной или более сложной, изогнутой формы, которые обладают удивительным свойством: при перегибании флексагонов их наружные поверхности прячутся внутрь, а раннее скрываемые поверхности неожиданно выходят наружу.
Комитет обнаружил, что, удлиняя цепочку треугольников, можно делать флексагоны с 9, 12, 15 и даже большим числом поверхностей. Таккерман изготовил действующую модель флексагона даже с 48 поверхностями! Он также обнаружил, что из зигзагообразной полоски бумаги можно сложить тетрагексафлексагон (с четырьмя поверхностями) и пентагексафлексагон (с пятью поверхностями). Существует три различных гексагексафлексагона: первый складывают из прямой полоски бумаги, второй - из полоски, сложенной в виде шестиугольника, и третий - из полоски, форма которой напоминает лист клевера.
Поверхностей может быть сколько угодно, даже 1 000 000, только такой флексагон будет почти невозможно крутить. И заготовку подобрать для такого флексагона очень сложно, потому что с каждым разом заготовки всё непонятнее.
2. Виды флексагонов
Исследуя данную тему, я столкнулся с огромным количеством видов флексагонов с очень длинными и пугающими названиями. Но всё оказалось очень просто.
Есть всего три вида флексагонов: тетрафлексагоны (тритетрафлексагон, гексатетрафлексагон, тетратетрафлексагон), гексафлексагоны (унагексафлексагон, дуогексафлексагон, тригексафлексагон, тетрагексафлексагон, пентагексафлексагон, гексагексафлексагон, гептагексафлексагон), флексотрубка.
Поверхности флексагона могут состоять из треугольников, квадратов, пятиугольников и т.д. Флексагон заданной формы с заданным количеством плоскостей может быть изготовлен из разных развёрток. При этом даже одна и та же развёртка может допускать разные варианты сворачивания. Общепринятой системы наименований для флексагонов нет. Мартин Гарднер использовал термины «тетрафлексагон» и «гексафлексагон» для обозначения флексагонов, состоящих из квадратов и треугольников соответственно, причём поверхности тетрафлексагона могли состоять из четырёх или шести квадратов. В результате рождается большое количество новых названий для флексагонов и иногда очень сложных для произношения.
Название флексагона содержит впереди числительное, показывающее, сколько плоскостей имеет этот флексагон, на втором месте — числительное, определяющее форму флексагона, и в заключение — известное уже слово, обозначающее, что всё это гнётся и складывается.
Вот несколько примеров приставок, образуемых из корней греческих числительных, применяемых для обозначений: 1– моно-, 2 – ди- или би-, 3 – три-, 4 – тетра-, 5 – пента-, 6 – гекса-, 7 – гепта-, 8 – окта- и т. д.
3. Плоские сгибаемые многоугольники
Тетрафлексагоны
Самый простой тетрафлексагон (флексагон с квадратными поверхностями) –тритетрафлексагон, имеющий три поверхности. В любой момент видимыми являются две из трёх поверхностей. Более сложные – гексатетрафлексагон и декатетрафлексагон – собираются из крестообразной развёртки без использования клея. Тетрафлексагоны с числом плоскостей 4n + 2 также можно изготавливать из квадратных рамок. Из зигзагообразных полосок бумаги можно изготовить тетратетрафлексагон и другие тетрафлексагоны с числом плоскостей, кратным 4.
Гексафлексагоны
Гексафлексагон – это флексагон, имеющий форму шестиугольника. Каждая поверхность флексагона состоит из шести треугольных частей.
Существует множество гексафлексагонов, различающихся по числу поверхностей. Известны гексафлексагоны с тремя, четырьмя, пятью, шестью, семью, девятью, двенадцатью, пятнадцатью, сорока восемью плоскостями; количество плоскостей ограничено только тем, что бумага имеет некоторую толщину.
4. Объёмные сгибаемые многогранники
Кольцевые флексагоны
Если флексагоны – это изгибаемые многоугольники, то кольцевой флексагон (флексор) – изгибаемый многогранник, собранный из «кольца» многоугольников.
Для наименования кольцевых флексагонов может быть использована приставка «цирко», например, пентациркодекафлексагон – кольцевой флексагон с пятью плоскостями, состоящими из десяти многоугольников (пятиугольников) каждая; тригемициркогексафлексагон – флексагон с тремя поверхностями, каждая из которых представляет собой кольцо (цирко) из половинок (геми) правильных шестиугольников (гекса).
Внешне флексоры выглядят привлекательнее, чем флексагоны, но математический интерес вызывает только кольцо из 8 тетраэдров, которое по-другому называют магическим. Математик Ройал В. Хит на заготовке для кольца из 8 тетраэдров расставил числа от 1 до 32 следующим образом:
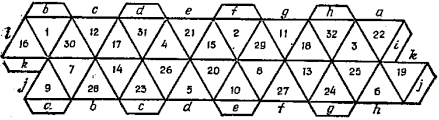
По этой заготовке изготавливается флексор. Он состоит из восьми тетраэдров. При вращении флексора, получаем четыре различные комбинации чисел с одним и тем же результатом:
1) 1+16+25+24+2+15+26+23=132; 2) 28+22+3+13+27+21+4+14=132;
3) 7+9+32+18+8+10+31+17=132; 4) 19+6+11+29+20+5+12+30=132;
Кроме этого, числа расположены так, что четыре грани каждого тетраэдра в сумме дают 66.
Объёмный тетрафлексагон
Объединив принципы тетрафлексагонов и флексоров, был создан объёмный тетрафлексагон.
Чтобы многогранник мог изгибаться, нужно выбрать тела, одинаковые со всех сторон. Выберем кубы, так как их удобнее взаимно прикреплять друг к другу, чем все остальные правильные многоугольники.
Пусть число кубов будет 8, так как тогда 4 куба смогут менять своё положение относительно двух других, что не получится при любом меньшем числе. Для цикличного проворачивания нужно так расположить шарниры, чтобы по окончании полного цикла поворота фигура могла начать этот цикл сначала, а не только повторять его в обратном порядке. Можно по-разному расположить 8 кубов симметрично центра всей фигуры:
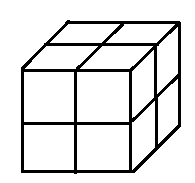
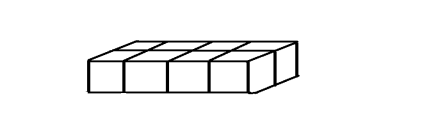
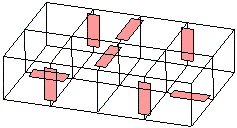
Будет лучше так расположить клапаны, чтобы эти два вида были этапом цикла изгибаний. Этого удалось добиться, расположив клапаны симметрично так, чтобы были соединены боковые, верхние и нижние кубы.
Флексотрубка.
Самую замечательную головоломку — флексотрубку — Стоун случайно открыл, работая над флексагонами, имеющими форму прямоугольного треугольника. («Для них, — сообщал он в одном письме, — мы не стали придумывать специального названия из соображений человеколюбия»). Построив плоский флексагон в форме квадрата, Стоун к своему изумлению обнаружил, что может превратить его в трубку. Как показали дальнейшие эксперименты, трубку можно полностью вывернуть наизнанку, если воспользоваться сложной системой сгибов по сторонам прямоугольных треугольников.
Глава II. Исследование флексагонов.
1. Наблюдения за свойствами флексагонов.
Теперь попробуем разобраться в схемах и инструкциях сборки флексагонов. На это ушло много времени, куча бумаги, и, конечно же, терпения. Не всё получалось сразу: то инструкции непонятные, то размеры неправильные. Пришлось серьёзно потрудиться, чуть ошибся – и начинай заново. Поэтапную сборку своих моделей я подробно отразил в приложении.
Когда фигура готова, нужно научиться раскрывать все её поверхности. Чтобы "открыть" гексафлексагон, его нужно одной рукой взять за два соседних треугольника, примыкающих к какой-нибудь вершине фигуры, а другой рукой потянуть за свободный край двух противоположных треугольников. При открывании флексагон выворачивается наизнанку, и наружу выходит поверхность, которая ранее скрывалась внутри.
Если в моделях с 3-мя, 4-мя, 5-ю поверхностями отыскать каждую поверхность не составило большого труда, то начиная с гексагексафлексагона, появились трудности. Флексагон можно было вращать до бесконечности, но увидеть пятую, шестую и так далее поверхности так и не удавалось! На помощь пришли статьи из журналов. Разобраться помогла схема, разработанная Таккерманом для гексагексафлексагона. Им был найден простейший способ выявления всех поверхностей любого флексагона: держа флексагон за какой-нибудь угол, следует открывать фигуру до тех пор, пока она открывается, а затем переходить к следующему углу. Этот метод так и называется «путь Таккермана». Он позволяет увидеть все шесть разворотов гексагексафлексагона за один цикл из 12 сгибаний. Стрелки указывают, в каком порядке становятся видимыми поверхности флексагона. Если модель перевернуть, то путь Таккермана будет изображаться той же схемой, но направление её обхода будет противоположным.
Пора попробовать ответить на вопрос: что же всё-таки такое флексагон - игрушка, оригами или математическая головоломка? Сначала обратимся за помощью к словарю:
Игрушка - предмет, предназначенный для игры. Воссоздавая реальные и воображаемые предметы, образы, игрушка служит целям умственного, нравственного, эстетического и физического воспитания.
Игрушка помогает ребёнку познавать окружающий мир, приучает его к целенаправленной, осмысленной деятельности, способствует развитию мышления, памяти, речи, эмоций. Игрушка широко используется в учебно-воспитательной работе с детьми, в частности для развития детского, технического и художественного творчества.
Головоломка - непростая задача, для решения которой, как правило, требуется сообразительность, а не специальные знания высокого уровня.
Оригами (яп. 折り紙, буквально «сложенная бумага») - вид декоративно-прикладного искусства; древнее искусство складывания фигурок из бумаги.
Для того чтобы ответить на поставленный вопрос, попробуем сами немного окунуться в искусство оригами. Фигурка оригами так же требует внимательного складывания листа бумаги по инструкции, но на этом процесс творчества заканчивается. А вот оригами-трансформеры очень близки к нашим флексагонам, они, перегибаясь, неожиданно создают новый вид, новую фигуру, но и здесь полёт фантазии заканчивается.
Прочитав специальную литературу, изучив природу флексагонов и флексоров, изготовив их, можно сделать вывод: в их основе лежит геометрия. Нельзя флексагоны и флексоры воспринимать как обычное оригами. Это выходит далеко за рамки привычного для нас бумагоскладывания и является геометрией. Этим вопросом занимались несколько известных математиков, поэтому флексагоны и флексоры – это, с одной стороны, занимательная математика, а с другой, доказательство того, что существуют многогранники, обладающие способностью изгибаться и ломаться.
Вспоминая всё, что мы узнали про флексагоны, можно сделать вывод, что это всё-таки занимательная геометрическая головоломка.
2. Применение флексагонов.
Флексагоны и флексоры применяются как средство математического развития дошкольников и школьников младших классов. Дети активно овладевают построением и использованием различных предметных, графических и мысленных моделей. Флексагоны, как средство математического моделирования, способствуют развитию мелкой моторики, пространственному воображению, памяти, вниманию, терпению и многому другому. Бывает иногда занимательно складывать флексагоны, выворачивать их, наблюдать, как они меняют форму и поворачиваются к нам разными комбинациями сторон.
Но однажды я случайно наткнулся на еще один необычный способ применения этих неординарных тел. Я даже не мог предположить, что кроме как в качестве игрушек они где-то ещё применяются. Но смотрите сами.
Флексор можно использовать в качестве фоторамки. На все треугольники одной поверхности приклеиваются фотографии (например, учеников класса). Этой фоторамке не требуется специальная подставка.
Необычно применение флексагона и в качестве шпаргалки. Написав на его сторонах формулы или правила, можно вывернуть флексагон обычными раскрашенными сторонами наружу.
Флексагоны и флексоры можно подарить друзьям в качестве сувенира или во время проведения праздника научить их делать эти геометрические игрушки.
Флексоры и простейшие флексагоны, раскрашенные в разные цвета или сделанные из фольги, можно использовать в качестве ёлочных украшений или для обычного оформления праздника.
Тетратетрафлексагон можно часто встретить в роли головоломки или рекламного буклета. Это связано с его особым свойством: одну из поверхностей отыскать гораздо сложнее, чем три других.
Широко применяется флексагон и при создании поздравительных открыток – трансформеров.
Большое применение объёмный многогранник может найти в дизайнерском искусстве, так как цикл перегибаний интересен при создании мебели – трансформера: диванов, кресел, стульев и других предметов.
В стиле флексагонов создаются интерьеры помещений и их декор.
Шарнир двойного действия, соединение которого присутствует на всех тетрафлексагонах, повсеместно используется для петель дверей и окон, в креплениях на настенные телевизоры, в раскладных телефонах.
Заключение
Закончена работа над исследовательским проектом. Пройден трудный, но интересный путь:
я познакомился с понятиями «флексагон» и «флексор»;
изучил вопрос о происхождении флексагонов;
нашел информацию и подробно изучил инструкции по конструированию отдельных видов флексагонов;
изготовил разнообразные модели флексагонов;
подготовил комплект развёрток флексагонов, по которым можно изготовить аналогичные модели;
познакомил одноклассников на уроке математики с флексагонами, где учащиеся попробовали сделать модель флексагона;
выявил области практического применения флексагонов в жизни человека.
Оглядываясь назад, можно с уверенностью сказать, что намеченные задачи выполнены, цель – изучение мира флексагонов – достигнута. Наша работа предназначена тем, кто любит необычную и занимательную математику. Также работа может быть использована на уроках математики: при изучении свойств треугольников, шестиугольников, тетраэдров или на занятиях математического кружка. В мире существует много неоткрытых загадочных вещей, которым ещё предстоит удивить нас своими замечательными свойствами.
© 2018, Агафонова Наталья Васильевна 9259 233
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
