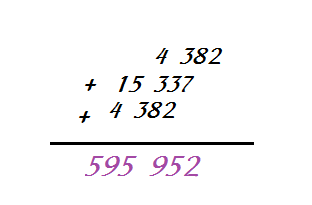Исследовательская работа "Различные способы умножения"

Оглавление

1. Введение 3 стр.

2. Основная часть

Немного из истории 4 стр.

Русский способ умножения 4 стр.

Китайский способ 5 стр.

Индийский способ 5 стр.

Палочки Непера 6 стр.

Умножение на пальцах 7 стр.

Новый способ умножения 7 стр.

1. Практическая часть 8 стр.

2. Заключение 9 стр.

3. Список литературы 10 стр.

4. Приложения 11 стр.

1. ВВЕДЕНИЕ

«Предмет математики настолько серьезен, что полезно не упускать случаев делать его немного занимательным». Б. Паскаль

Мы живём XXI веке, веке развития вычислительной техники и новых технологий. Мы уже привыкли к тому, что многое за нас делают компьютеры и машины. Относительно производства, конечно, это удобно и результат работы получается качественнее, чем ручной. Думаем, что процесс вычислений может быть интересным. Нас заинтересовал вопрос о том, как же считали наши предки, какие существовали способы счета в разные века. Существует ли способ умножения, который окажется легче и быстрее, нежели способы, которым нас научили в школе. Кроме того, нас заинтересовал вопрос о том, а знают ли ребята из нашей школы, что умножать можно по-разному, даже на пальцах.

Цель: Изучить различные способы умножения, выбрать для себя самые интересные методы умножения и исследовать, есть ли более легкие и быстрые способы, чем те, которые предлагаются в школе.

Задачи:

-Изучить различные способы умножения, для применения которых, достаточно устного счета или использования карандаша, ручки и бумаги.

-Найти как можно больше  необычных способов вычислений.

-Научиться их применять.

-Исследовать удобство этих методов и возможность их применения на практике.

Объекты исследования: Способы умножения от древности до современности.

Гипотеза:

-Существуют интересные способы умножения, с развитием прогресса, развивались методы умножения.

1. ОСНОВНАЯ ЧАСТЬ

Немного из истории

Известные нам сегодня способы вычислений не всегда были такими удобными и простыми. В далекие от наших дней времена приемы вычислений были более громоздкими, медленными. Перенесись современный школьник на пять веков назад, и предки были бы поражены быстротой и точностью его вычислений. Он превзошел бы самых известных счетчиков того времени, о нем говорили бы окрестные школы, монастыри, каждый желал бы научиться счету у нового мастера.

 Самыми сложными в старину считались действия умножения и деления.

В те времена не было какого-либо одного приема для действий умножения и деления. Одновременно использовалось около дюжины различных способов умножения и деления. Каждый прием был сложный запутанный, человеку средних способностей запоминать их было невозможно. Каждый учитель того времени выбирал один прием и использовал только его в своем деле.

         В. Беллюстин в своей книге «Как постепенно дошли люди до настоящей арифметики»  рассказывает о 27 способах умножения, причем автор замечает, что, скорее всего, нам известны далеко не все способы, большая их часть затеряна именно в рукописных вариантах.

    Рассмотрим наиболее интересные и простые  способы умножения.

Русский способ умножения

Данный способ появился в глубокой древности и использовался русскими крестьянами. Суть русского способа умножения состоит в следующем: умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, при этом параллельно удваивают другое число. Последнее удвоенное число и дает нужный результат.

Таким образом, результат умножения не изменится, если один множитель уменьшить в два раза, а другой в два раза увеличить.

Например, умножим 67 на 25. Запишем данные числа на одной строчке, между ними проведем вертикальную черту. Число, стоящее слева, будем делить на 2, а число, стоящее справа, на 2 умножать. Если при делении получается остаток, то его отбрасывают. Деление заканчивается тогда, когда слева появится 1, вычеркиваем строки, в которых слева четные числа. Оставшиеся справа числа складываются – это результат.

К последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечётных чисел левого столбца – сумма и будет произведением, которое ищут.

Таким образом, все строки с четными числами, стоящими слева зачеркиваем, после чего складываем не зачеркнутые числа, стоящие в правом столбце (Приложение №1).

Китайский  способ умножения

Интересен китайский способ умножения. Это графический способ. Таблицу умножения помнить не нужно, так же не нужно запоминать цифры при переносе в разряд. Необходимо лишь сосчитать пересечение линий.

Например, умножим 11 на 12.

Рисуем линии следующим способом: у первого множителя десятков 1 линии сверху, число единиц – 1 линия ниже.   Линии второго множителя должны пересекать линии первого множителя. У второго множителя 1 линия левее (число десятков) две линии правее (по числу единиц) (Приложение №2).

Индийский способ умножения

Известный арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль - Хорезми жил и работал в Багдаде. Учёный работал в Доме мудрости, где были библиотека и обсерватория, здесь работали почти все крупные арабские учёные.
Сведений о жизни и деятельности Мухаммеда аль - Хорезми мало. Сохранились лишь две его работы – по алгебре и по арифметике. В последний из этих книг даны четыре правила арифметических действий, почти такие же, что используются в наше время.
В своей «Книге об индийском счете» учёный описал способ, придуманный в Древней Индии, а позже названный «методом решётки».

Пусть необходимо умножить 576 на 98.

Рисуется табличка из трех столбцов (так как число 576 – трехзначное)
и двух строк (98 – двузначное число), каждая клетка разделена диагональю. Цифры чисел 576 и 98 записываются, соответственно, над табличкой и справа от нее.

Рисунок 2

После этого в каждую клетку записывается произведение цифры, стоящей в соответствующем столбце сверху, на цифру в соответствующей строке справа, причем десятки и единицы произведения разделяются диагоналями ячеек.

Теперь можно определить результат умножения. Для этого необходимо просуммировать цифры по наклонным полоскам справа налево,
при необходимости перенося «в уме» в соседнюю слева полоску
единицу или двойку и записывая эти суммы слева и снизу.

Результат следует читать вначале слева от таблички сверху вниз,
а затем под табличкой слева направо – он равен 56 448 (Приложение №3) .

Этот же метод использовался в Италии в средние века и может называться итальянским или «Решетчатое умножение».

Неудобства этого способа заключаются в трудоёмкости построения прямоугольной таблицы, а сам процесс умножения интересен и заполнение таблицы напоминает игру.

Палочки Непера

Способ умножения решеткой положен в основу счетного прибора, описанного шотландским математиком Джоном Непером (изобретателем логарифмов) в 1617 году. Этот простой счетный прибор в дальнейшем получил название «палочки Непера».

Прибор представлял собой набор прямоугольных пластин (палочек), в который входили:

• палочки с результатами умножения всех чисел от 0 до 9 на числа от 0 до 9; сверху каждой палочки наносилось число от 0 до 9. Результат умножения на палочках представлен двумя цифрами (в том числе начальным нулем), разделенными наклонной чертой;

• одна палочка с нанесенными на нее цифрами от 1 до 9 (указатель строк).

Пример умножения чисел с помощью палочек Непера подробно описан в приложении №4.

Умножение на пальцах

Древние египтяне были очень религиозны и считали, что душу умершего в загробном мире подвергают экзамену по счёту на пальцах. Умножали на пальцах однозначные числа от 6 до 9. Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходил число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. После этого брали столько десятков, сколько вытянуто пальцев на обеих руках, и прибавляли к этому числу произведение загнутых пальцев на первой и второй руке. Пример умножения на пальцах описан в приложении №5.

Новый способ умножения

Познакомились мы и с таким способом умножения как «новый». Нам он показался довольно интересным. Изобрел его Василий Оконешников кандидат философских наук. По его мнению,  человек может запомнить большой запас информации, главное – как эту информацию расположить.  Он считает, что наиболее эффективной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.

Оконешниковым создана специальная таблица (Приложение №6). Цифры в ней распределены в девяти клетках непросто.

Таблица разделена на 9 частей. Расположены они по принципу мини калькулятора: слева в нижнем углу «1», справа в верхнем углу «9». Каждая часть – таблица умножения чисел от 1 до 9 (опять же в левом нижнем углу на 1, рядом правее на 2 и т.д., по той же «кнопочной» система).

Как же пользоваться этой таблицей?

Например, требуется умножить 9 на 842. Сразу вспоминаем большую «кнопку» 9 (она вверху справа и на ней мысленно находим маленькие кнопочки 8,4,2 (они также расположены как на калькуляторе). Им соответствуют числа 72, 36, 18. Полученные числа складываем особо: первая цифра 7 (остаётся без изменения), 2 мысленно складываем с 3, получаем 5 – это вторая цифра результата, 6 складываем с 1, получаем третью цифру -7, и остаётся последняя цифра искомого числа – 8. В результате получилось 7578.

Если при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.

Новая методика была опробована в нескольких российских школах и университетах. Считать по такой таблице не сложно.

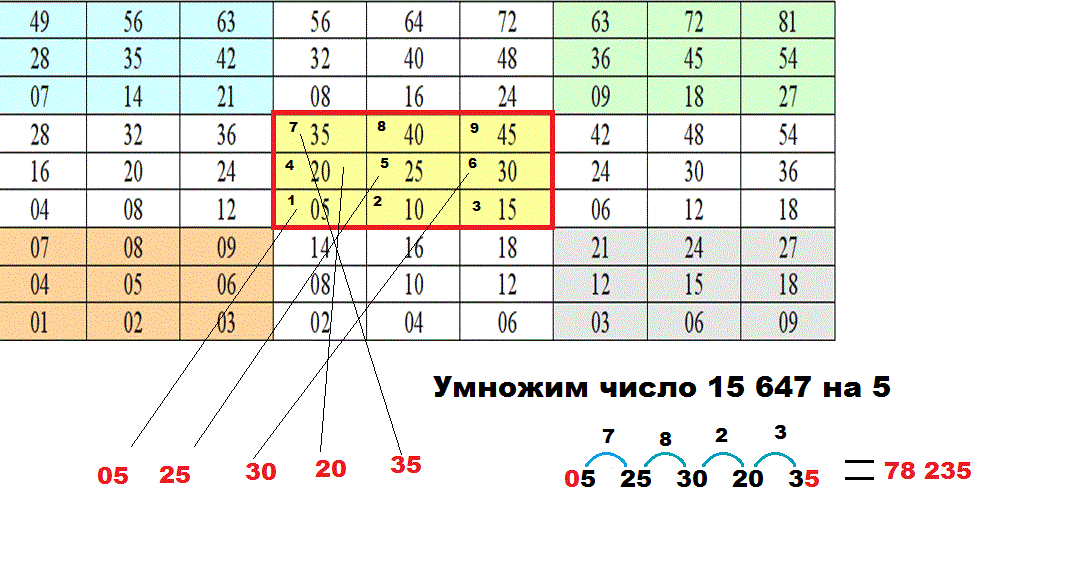
Например, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35

Левую цифру (в нашем примере - ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.

В итоге получаем: 078235. Число 78235 и есть результат умножения.

Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место (Приложение №7).

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Применение различных способов умножения на практике

Мы сравнили время, которое нам потребовалось для получения произведения, чисел 24 567 и 132 при использовании индийского, обычного умножения «в столбик» и «нового» способа умножения. При умножении в столбик затрачено 1 мин 22 сек, полученный результат 3242844.

При умножении индийским способом затрачено 2 мин 07 сек, полученный результат 3242844. При умножении «новым» способом затрачено 3 мин 46 сек, полученный результат 3242844. Самым быстрым способом оказался тот, который мы используем в школе.

Результаты опроса

Нами был проведен опрос. Учащимся нашей школы было предложено ответить на вопрос, знают ли они, что «на пальцах» можно не только складывать, но и умножать. Результат оказался следующим:

1. Не знают, что это возможно – 6 человек.

2. Слышали, что это можно – 11 человек.

3. Знают и применяют на практике – 2 человека.

1. ЗАКЛЮЧЕНИЕ

Научившись считать всеми представленными способами, пришли  к выводу: что самые простые способы это те, которые мы изучаем в школе. Возможно, что они для нас просто более привычны.

Из всех найденных необычных способов счета более интересным показался индийский способ или способ «решетчатого умножения».

Самым простым нам показался «русский» способ умножения, который использовали русские крестьяне. Теперь мы применяем его при умножении не слишком больших чисел.

Думаем, что и наш способ умножения в столбик не является совершенным и можно придумать еще более быстрые и более надежные способы, и возможно, в будущем школьники будут пользоваться другими методами.

1. СПИСОК ЛИТЕРАТУРЫ

1.  Депман И. «Рассказы о математике».  – Ленинград. Просвещение, 1954. – 140 с.

2. Корнеев А.А.  «Феномен русского умножения. История». – URL: http://numbernautics.ru/

3. Олехник  С. Н., Нестеренко Ю. В., Потапов М. К.  «Старинные занимательные задачи». –  М.: Наука. Главная редакция физико-математической литературы, 1985. – 160 с.

4. Перельман Я.И. Быстрый счет. Тридцать простых приемов устного счета. Л., 1941 – 2 с.

5. Перельман Я.И.  Занимательная  арифметика. М.Русанова,1994--205с.

1. ПРИЛОЖЕНИЯ

Приложение №1

Русский способ умножения

Умножаем число 67 на 25:

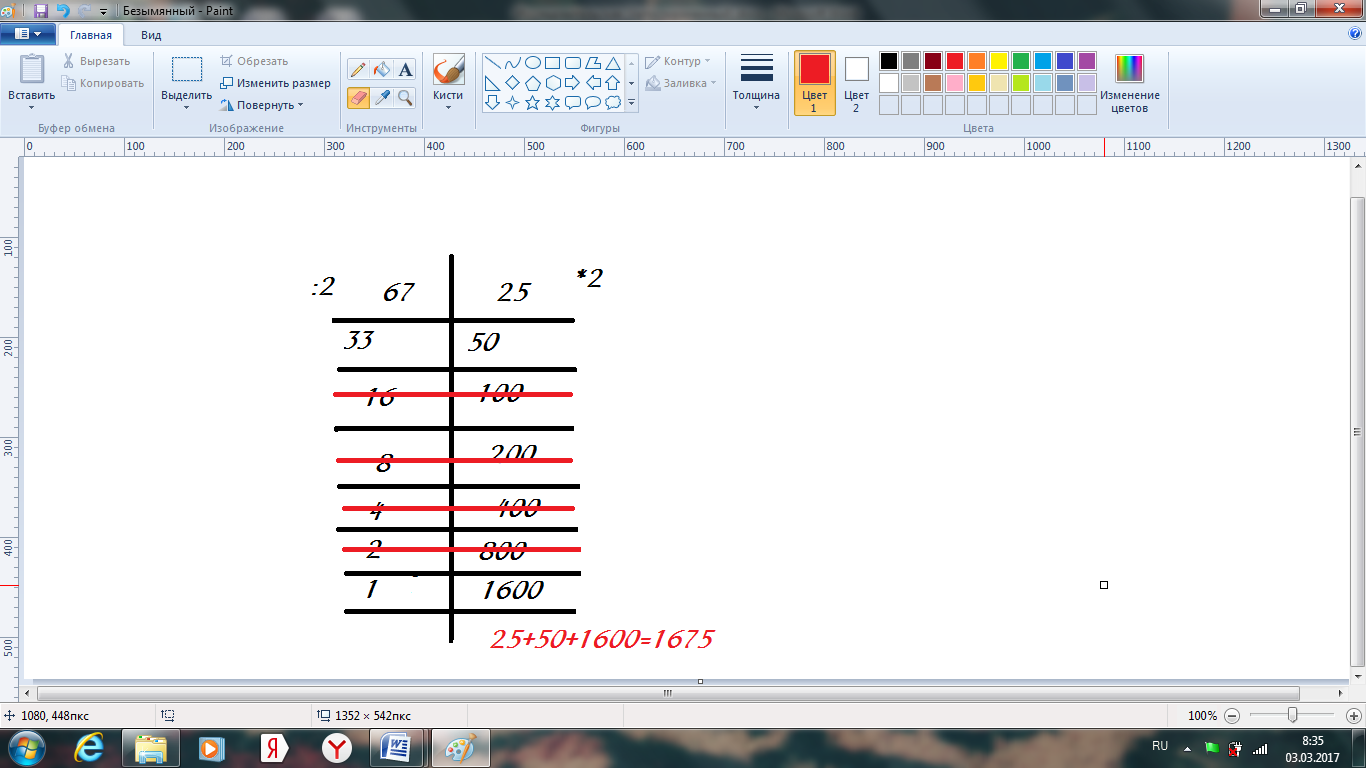
Ответ: 1675.

Приложение №2

Китайский способ умножения

Умножаем китайским способом числа 11 и 12:

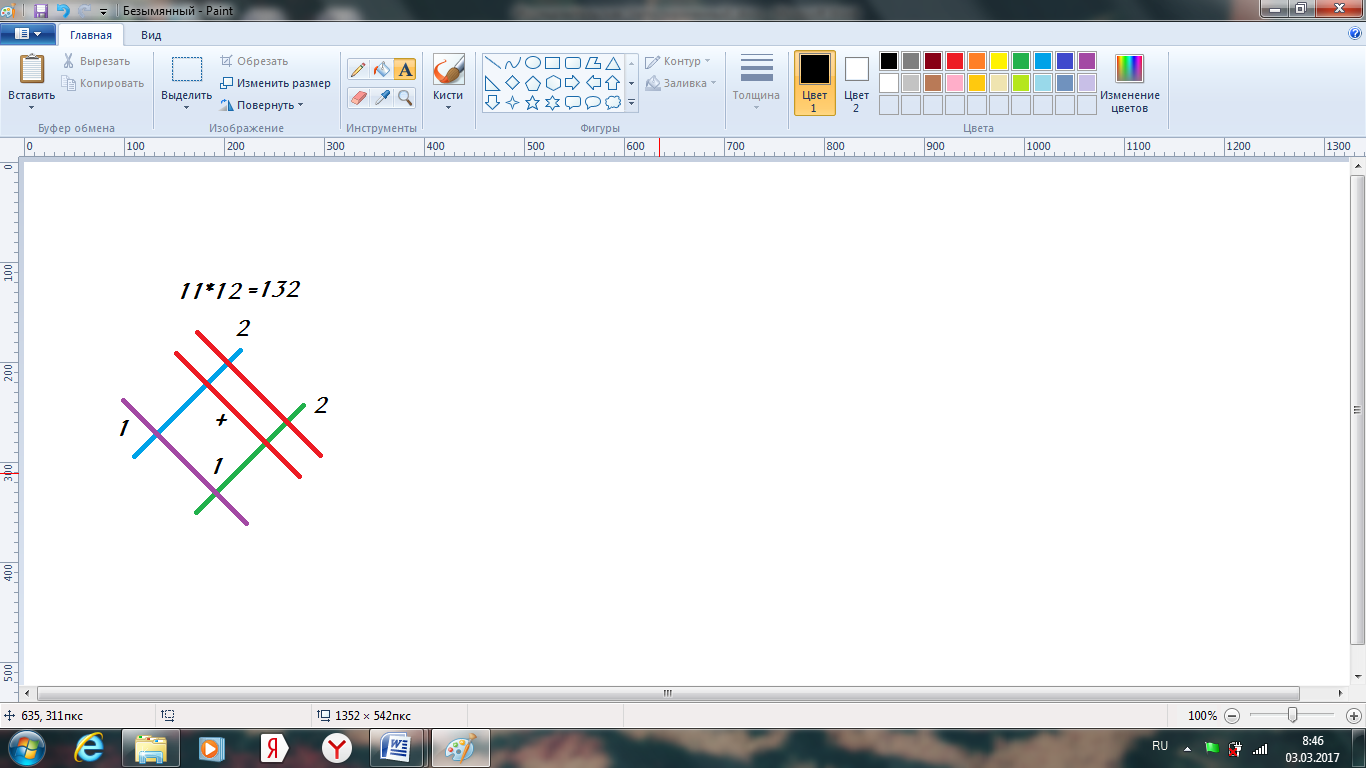
Ответ: 132.

Приложение №3

Индийский способ умножения

Умножаем индийским способом числа 576 и 98:

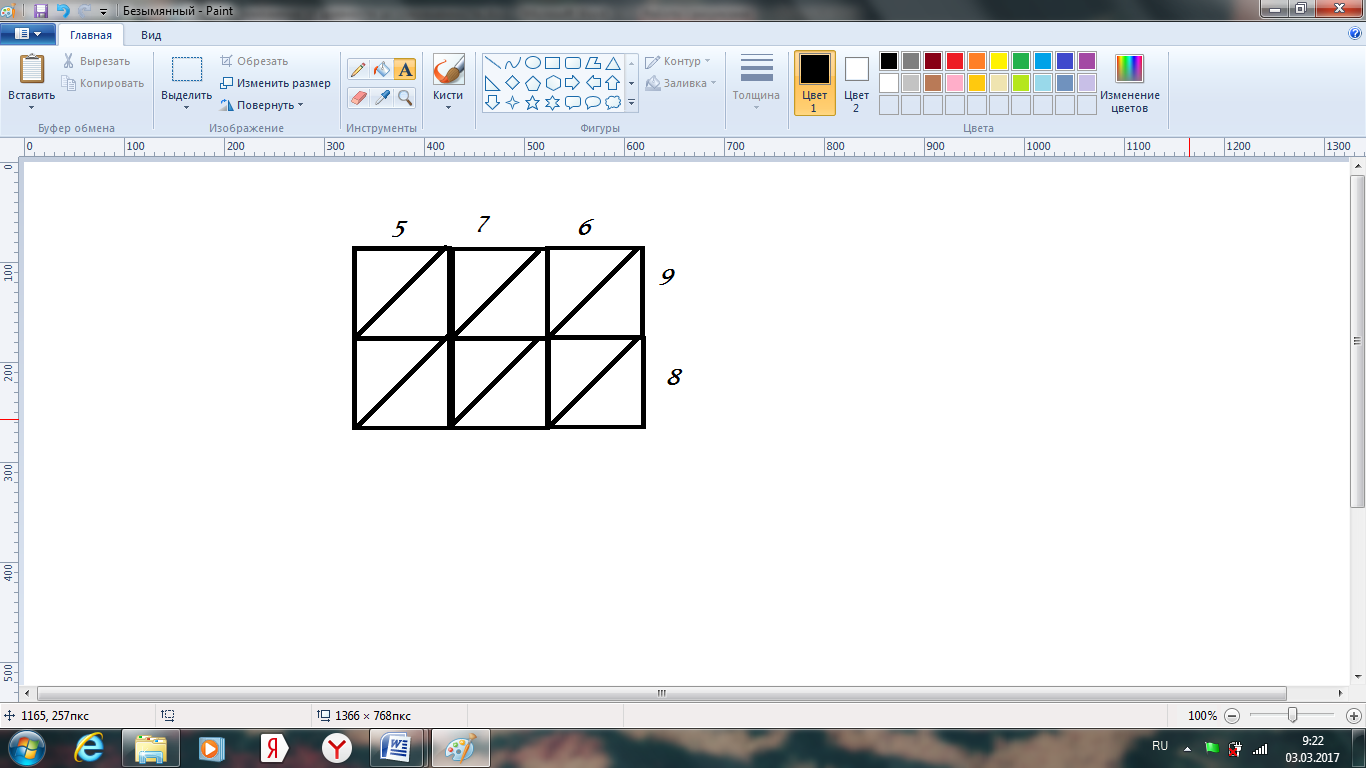
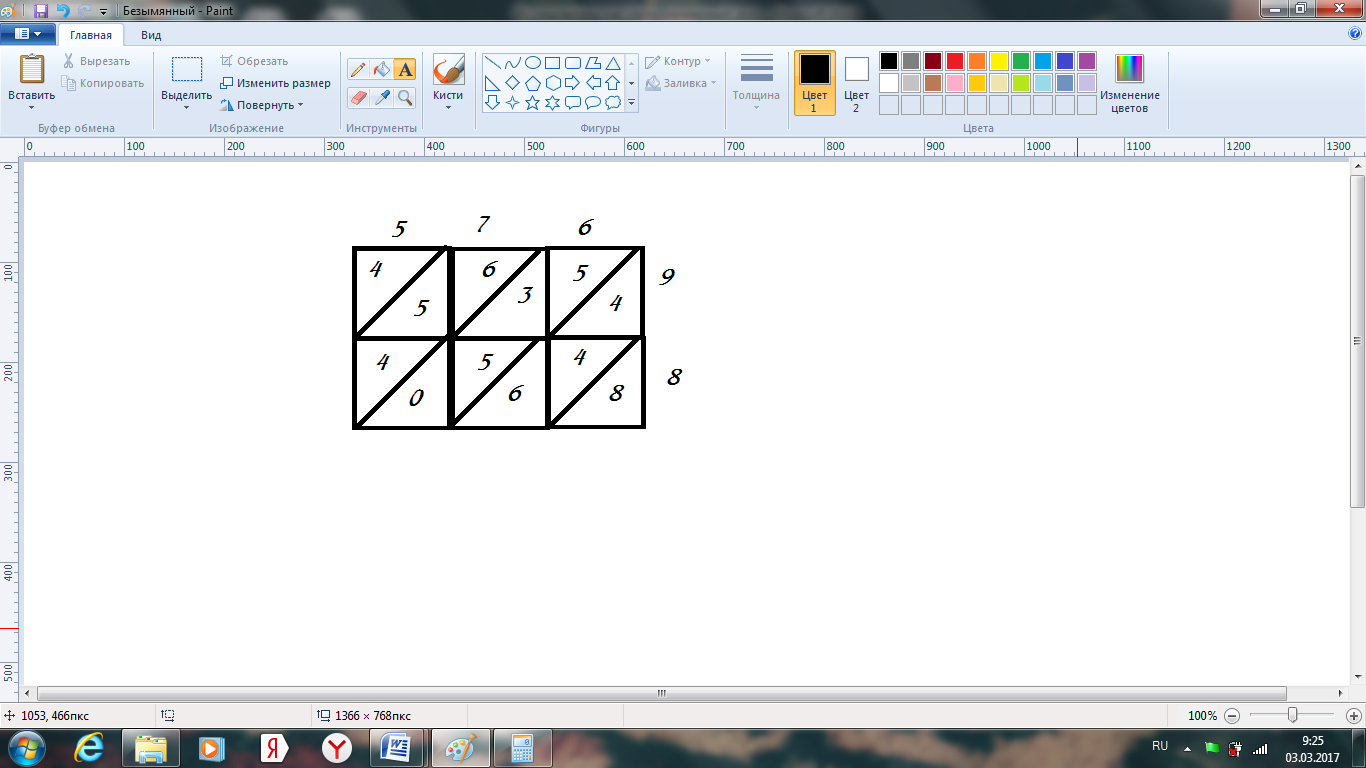
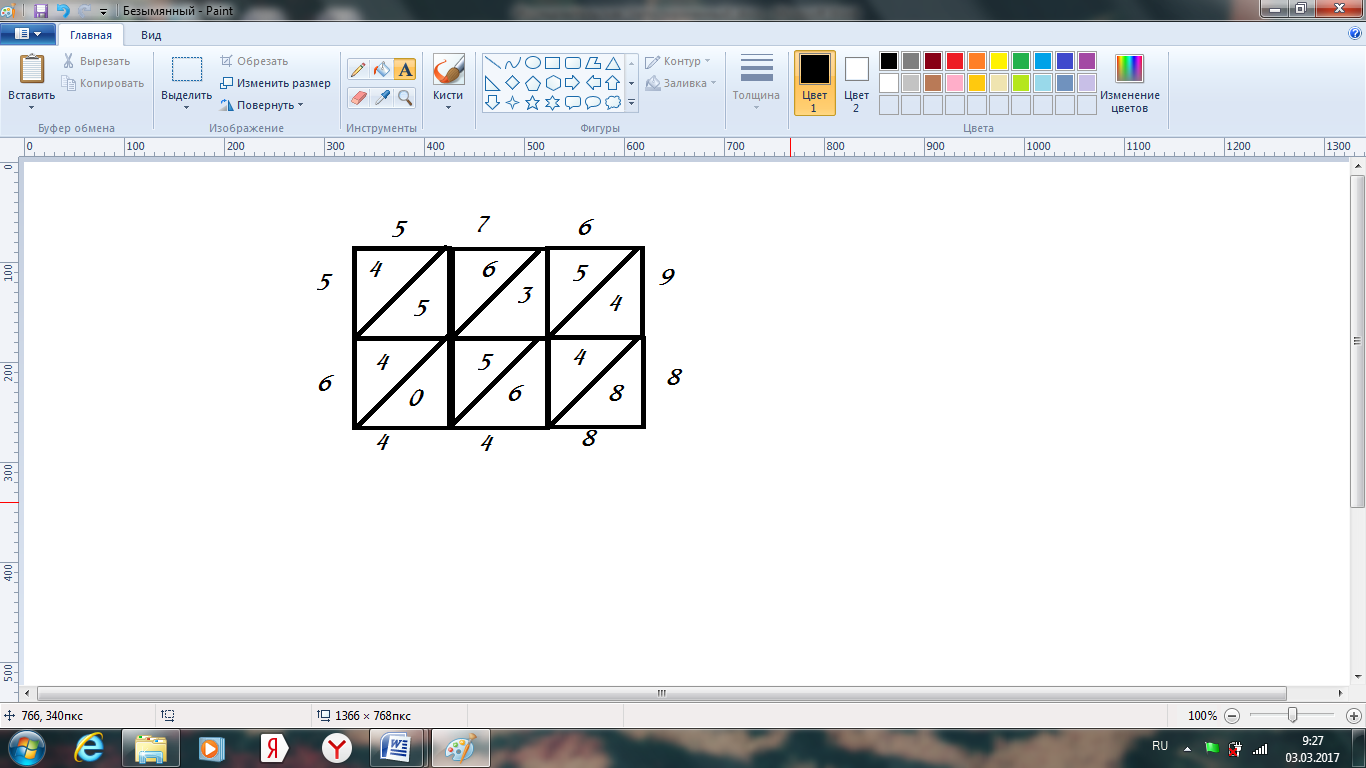
Ответ: 56 448.

Приложения №4

Умножение с помощью палочек Непера

Умножим числа 2191 и 272 с помощью палочек Непера.

1. Палочки, соответствующие значениям каждого разряда множимого, выкладываются в ряд так, чтобы цифры сверху каждой палочки составляли множимое.

2. Слева прикладывается палочка – указатель строк, по которой выбирают строки, соответствующие разрядам множителя.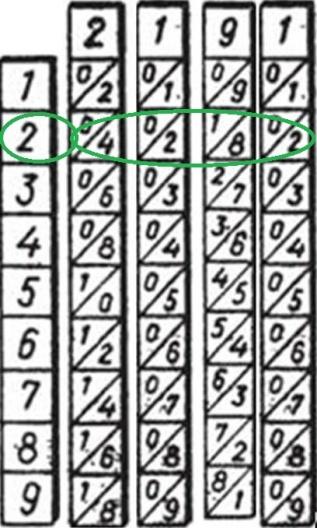

3. Результат умножения числа 2191 на 2.

На данном шаге обращаем внимание на строчку 2. Данная строка заканчивается цифрой 2, это и есть последняя цифра нашего произведения. Далее необходимо просуммировать цифры по наклонным полоскам справа налево, при необходимости перенося «в уме» в соседнюю слева полоску единицу или другое число.

Таким образом, получаем на данном шаге следующий результат умножения 2191 на 2 – 4 382.

1. Аналогично находим результат умножения 2 191 на 7. Получаем 15 337.

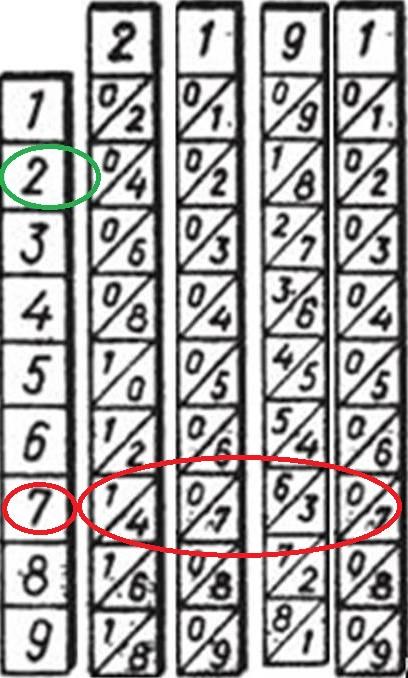
1. Складываем все полученные результаты, учитывая порядок разряда, получаем искомое произведение:

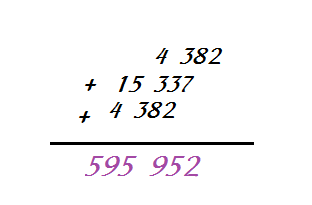
Приложение №5

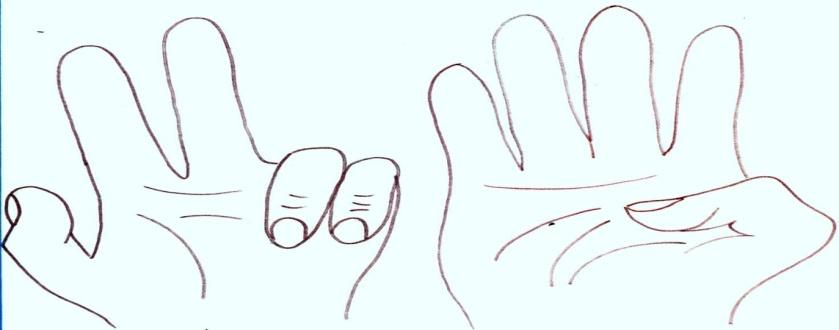
Умножение на пальцах

Пример умножения на пальцах чисел 8 и 9, 8 ∙ 9 = 72. На одной руке нужно вытянуть 3 пальца, так как 8 больше 5 на 3. На второй руке вытягиваем 4 пальца, так как 9 превосходит число 5 на 4. Вытянутые пальцы на обеих руках – это число десятков, а количество согнутых пальцев на обеих руках умножают, таким образом получая число единиц.

Приложение №6

Новый способ умножения

Таблица Василия Оконешникова имеет следующий вид:

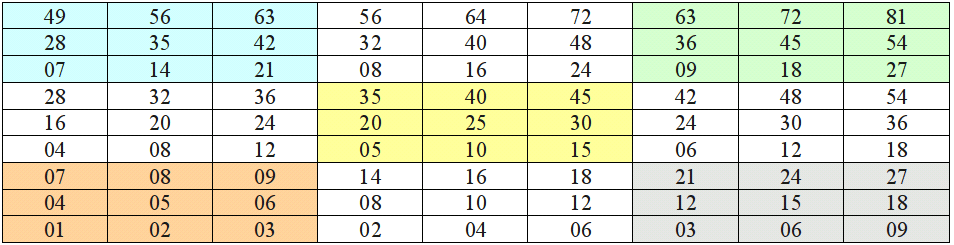
На рисунке приведен пример умножения чисел 15 647 и 5.

Приложение №7

Результаты применения различных способов умножения

Результаты опроса

13