8 класс Итоговый тест.
Вариант 1.
Часть 1.
А1. Выполните деление  .
.
Ответ:___________
А2. Расположите числа 
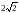 , 3 в порядке возрастания.
, 3 в порядке возрастания.
1). 
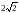 , 3. 2).
, 3. 2). 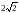 ,
, 3. 3). 3,
3. 3). 3, 
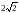 . 4).
. 4). 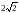 , 3,
, 3, 
А3. Укажите выражение, не имеющее смысла.
1). . 2).
. 2).  . 3).
. 3).  . 4).
. 4). 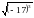 .
.
А4. Решите уравнение 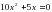 .
.
1). 0; -2. 2). 0;  . 3).
. 3).  ;
;  . 4). 0,
. 4). 0, 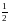 .
.
А5. Найдите положительный корень уравнения  .
.
1). 2. 2). 5. 3). 1. 4). 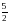 .
.
А6. Лыжник от озера до деревни шел со скоростью 15 км/ч, а обратно – со скоростью 12 км/ч. Сколько времени ушло у него на обратную дорогу, если на весь путь туда и обратно лыжник затратил 3 ч?
Пусть x ч – время, затраченное на обратную дорогу. Какое из уравнений соответствует условию задачи?
1). 2). . 3). 4). .
А7. Решите неравенство  7х+5
7х+5
1).  . 2).
. 2).  . 3).
. 3).  . 4).
. 4).  .
.
А8. На каком рисунке изображено решение системы неравенств  ?
?

 1).
1).  \\\\\\\\\\\\\\\\\\\\\\ 2).
\\\\\\\\\\\\\\\\\\\\\\ 2).  \\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\
-1 3

 3).
3).  \\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\ 4). \\\\\\\\\\\\
4). \\\\\\\\\\\\
-1 3 -3
А9. Вычислите значение выражения 
1) 6. 2)  3)
3)  4) -6
4) -6
А10. Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 5.

А11. Используя данные, указанные на рисунке, найдите тангенс угла Р.


 1).
1). . 2).
. 2).  . 3).
. 3).  . 4).
. 4).  . К
. К
4 5


М 3 Р
А12. Из точки В к окружности с центром О проведена касательная, А – точка касания.
Найдите радиус окружности, если АВ=  , ОВ=6.
, ОВ=6.
Ответ:____________________
Часть 2.
В1. Решить уравнение  .
.
В2.. Найти наибольшее целое значение а, при котором сумма дробей и положительна.
Часть 3.
С1. В параллелограмме ABCD проведены биссектрисы углов А и D, которые пресекаются в
точке на стороне ВС. Найдите периметр параллелограмма АВСD, если АВ= 6 см.
С2. При каких значениях  уравнение
уравнение  имеет один корень?
имеет один корень?
8 класс Итоговый тест.
Вариант 2.
Часть 1.
А1. Упростите выражение  .
.
Ответ: _____________
А2. Расположите числа 
 , 4 в порядке возрастания.
, 4 в порядке возрастания.
1). 
 , 4. 2).
, 4. 2).  , 4,
, 4,  . 3). 4,
. 3). 4, 
 . 4).
. 4).  4,
4, 
А3. Какое выражение не имеет смысла?
1).  . 2).
. 2).  . 3).
. 3).  . 4).
. 4).  .
.
А4. Решите уравнение  .
.
1). 4; -4. 2). -2;2. 3). 2. 4). 4.
А5. Найдите отрицательный корень уравнения  .
.
1).  . 2). -2. 3). -8. 4). -1.
. 2). -2. 3). -8. 4). -1.
А6. Велосипедист от озера до деревни ехал со скоростью 15 км/ч, а обратно со скоростью 10 км/ч. Сколько времени у него ушло на дорогу от озера до деревни, если на весь путь туда и обратно велосипедист затратил 1ч?
Пусть x ч – время, затраченное на дорогу от озера до деревни. Какое уравнение соответствует условию задачи?
1). 2). . 3). 4). .
А7. На каком рисунке изображено решение неравенства  ?
?
1). 2).



 \\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\\ \\\\\\\\\\\\\\\\
-4 -4

 3).
3).  \\\\\\\\\\\\\\\\ 4).\\\\\\\\\\\\\\\\
\\\\\\\\\\\\\\\\ 4).\\\\\\\\\\\\\\\\
3 3
А8. Решите систему неравенств 
1). Нет решений. 2).  . 3).
. 3).  . 4).
. 4).  .
.
А9. Вычислите значение выражения 
1)  2)
2)  3) 16 4) -16
3) 16 4) -16
А10. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

А11. Используя данные, указанные на рисунке, определите катет PN.

 1).
1).  . 2).
. 2).  . О
. О
3). 4. 4).  . 60о
. 60о


 Р N
Р N
А12. АВ – диаметр окружности, точка К лежит на окружности,  .Найдите
.Найдите
Угол ВАК.
Ответ:_____________________
Часть 2.
В1. Решить уравнение.  .
.
В2. Найти наименьшее целое значение а, при котором разность дробей и отрицательна.
Часть 3.
С1. AВCD – равнобедренная трапеция. M, N, P, Q – середины сторон. Определите вид
четырехугольника MNPQ.
С2. При каких значениях  уравнение
уравнение  имеет два корня.
имеет два корня.
Критерии оценивания.
На выполнение работы отводится 1 час.
Оценка «3» ставится за верно решенных 8-11 заданий из 1 части.
Оценка «4» ставится за верно выполненные 11 заданий 1 части и одно задание второй или третьей части.
Оценка «5» ставится за верно выполненные 11 заданий 1 части, 1 задание второй части и 1 задание третьей части.







 .
.
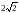 , 3 в порядке возрастания.
, 3 в порядке возрастания. . 2).
. 2).  . 3).
. 3).  . 4).
. 4). 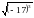 .
.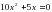 .
. . 3).
. 3).  ;
; 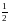 .
. .
.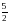 .
. 7х+5
7х+5  . 2).
. 2).  . 3).
. 3). 









