Измерение информации. Алфавитный и содержательный подходы.

Тема: «Измерение информации. Алфавитный и содержательный подходы»

Преподаватель информатики Отева О.А.

Объемный подход измерения информации

• Объем информации не связан с ее содержанием.
• Когда говорят об объеме информации, то имеют в виду размер текста в том алфавите, с помощью которого эта информация представлена.
• Объемный способ измерения информации называют еще алфавитным подходом.

Алфавитный подход к измерению информации

Алфавитный подход к измерению количества информации основан на подсчете числа символов в сообщении.

При алфавитном подходе к определению количества информации отвлекаются от содержания информации и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.

Все множество используемых в языке символов будем традиционно называть алфавитом.

Полное количество символов алфавита принято называть мощностью алфавита.

Одним из основоположников алфавитного подхода к измерению информации является Андрей Николаевич Колмогоров, (1903-1987), великий российский ученый - математик.  

Двоичное кодирование текстовой информации

33 русских прописных буквы +

33 русских строчных букв + 26 английских строчных букв + 26 прописных английских букв + 10 цифр + знаки препинания + скобки и знаки математических операций + специальные символы (@, #, $, %, &, *) + знаки псевдографики ≈ 256 символов.

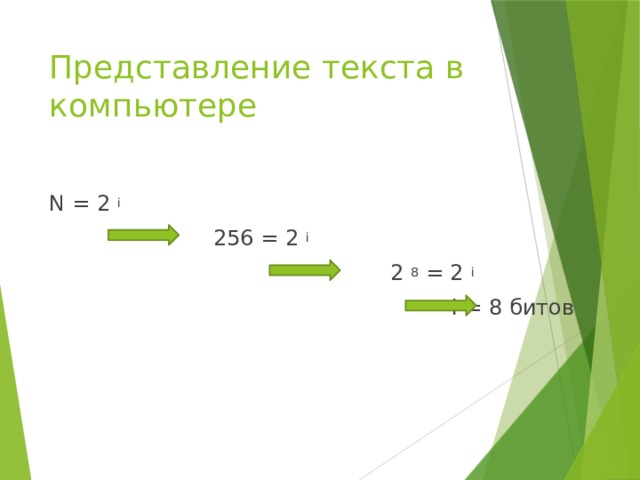
Представление текста в компьютере

N = 2 i

256 = 2 i

2 8 = 2 i

i = 8 битов

Единицы измерения

В двоичном коде один двоичный разряд несет одну единицу информации, которая называется 1 бит.

• При двоичном кодировании объем информации, выраженный в битах, равен длине двоичного кода, в котором информация представлена.

Более крупная единица измерения информации является байт: 1 байт = 8 битов

• Информационный объем текста в памяти компьютера измеряется в байтах. Он равен количеству знаков в записи текста.

Например, лист формата А4 кегля 12 - 4000 байтов, т.е. примерно 4000 знаков.

N = 2 I – формула для решения задач на информационный подход к измерению информации,

где

• N – мощность алфавита
• i – количество информации одного символа 
• I = K*i - информационный объем сообщения
• K - количество символов в сообщении

Содержательный подход к измерению информации

Основоположником содержательного подхода к измерению информации является американский учёный Клод Элвуд Шеннон (1916 — 2001). По Шеннону, информация — уменьшение неопределенности наших знаний. Неопределенность некоторого события — это количество возможных исходов данного события.

Возможные Произошедшее события событие

Единицы измерения информации

За единицу количества информации принимается такое количество информации, которое содержит сообщение, уменьшающее неопределенность знания в два раза. Такая единица названа бит.

Так, например, если из колоды карт наугад выбирают карту, то неопределенность равна - ?.

При бросании монеты неопределенность равна -?.

При бросании кубика неопределенность равна - ?. 

Бит – наименьшая единица представления информации Байт – наименьшая единица обработки и передачи информации

• 1 байт = 2 3 битов = 8 битов
• 1 Килобайт (Кбайт) = 1024 байт = 2 10  байт
• 1 Мегабайт (Мбайт) = 1024 Кбайт = 2 20  байт
• 1 Гигабайт (Гбайт) = 1024 Мбайт = 2 30  байт
• 1 Терабайт (Тбайт) = 1024 Гбайт = 2 40  байт
• 1 Петабайт (Пбайт) = 1024 Тбайт = 2 50  байт

Для перевода из крупных единиц в мелкие числа умножают, согласно таблице переводов

Пример:

2 Кбайта = 2 * (1 Кбайт) = 2 * 1024 байтов = 2048 байтов = 2048 * 8 бит = 16384 бита.

Для перевода количества информации из мелких единиц в более крупные нужно делить.

Пример:

8192 бита = 8192 : 8 = 1024 байт = 1024 : 1024 (т.к. в 1 Кбайте 1024 байт) = 1 Кбайт

Примеры объемов информации

• Страница книги 2,5 Кбайт
• Учебник 0,5 Мбайт
• Газета 150 Кбайт
• Черно-белый кадр 300 Кбайт
• Цветной кадр из 3 цветов 1 Мбайт
• 1,5 часовой цветной фильм 135 Гбайт

1. Сообщение, записанное буквами из 128 – символьного алфавита, содержит 30 символов. Какой объем информации оно несет?

I = K*i

N = 2 i

N = 128

К = 30

I = 30*7

128 = 2 i

I - ?

I = 210 бит

i = 7 бит

2. Объём информационного сообщения 200 бит. В сообщении 25 символов. Какова мощность алфавита?

N = 2 i

I = K*i

i = I/K

N = 2 4

i = 200/25 = 4битa

N = 16 символов

I = 200 бит

К = 25

N - ?

6. Сколько информации несет сообщение о том, что было угадано число в диапазоне целых чисел от 684 до 811?

7. В школьной библиотеке 16 стеллажей с книгами, на каждом – по 8 полок. Ученику сообщили, что нужный учебник находится на 2-ой полке 4-го стеллажа. Какое количество информации получил ученик?

8. Поле для игры в крестики-нолики содержит 64 клетки. Первый игрок ставит крестик в любую клетку. Какое количество информации получит второй игрок при первом ходе первого игрока?

Домашнее задание

• Сколько бит информации содержит сообщение о том, что на экзамене ученик вытянул билет №14, а всего экзаменационных билетов было 32?

• При угадывании целого числа из интервала от 10 до N получено 7 бит информации. Укажите максимально возможное значение N.

• В корзине лежат шары. Все разного цвета. Сообщение о том, что достали синий шар, несёт 5 бит информации. Сколько всего шаров было в корзине?

Литература:

Название:  Информатика и ИКТ 10-11 классы Автор(ы):  И.Г. Семакин, Е.К. Хеннер Год издания:  2013 Издательство:   Бином Количество страниц:  249