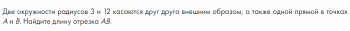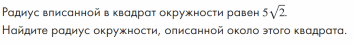Предмет:Геометрия
Класс: 8
Тема:Касание окружностей
Библиотека ЦОК https://m.edsoo.ru/8a1410a8
Цели:
Урок по предмету «Геометрия» для 8 класса по теме «Взаимное расположение двух окружностей. Касание двух окружностей».
Контролируемые элементы содержания
Взаимное расположение прямой и окружности, двух окружностей
Контролируемые умения
Развитие пространственных представлений, изобразительных умений, навыков геометрических построений
Проверяемые элементы содержания
Взаимное расположение прямой и окружности, двух окружностей
Предметные умения
Распознавать геометрические фигуры на плоскости, определять их взаимное расположение, изображать геометрические фигуры
Личностные результаты
Овладение основными навыками исследовательской деятельности, установка на осмысление опыта, наблюдений, поступков и стремление совершенствовать пути достижения индивидуального и коллективного благополучия
Функциональная грамотность
Связывать между собой различные элементы знания и связанную с ними информацию, а также способы решения задачи
Тип урока:Урок освоения новых знаний и умений.
На уроке предусмотрено использование следующих электронных образовательных материалов:«Галерея изображений (группа изображений по одной тематике)», «Самостоятельная работа».
Ключевые слова
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ОКРУЖНОСТИ
ДВУХ ОКРУЖНОСТЕЙ
Ход урока:
-
Вхождение в тему урока и создание условий для осознанного восприятия нового материала:
1) «Знание – самое превосходное из владений.
Все стремятся к нему,
само же оно не приходит».
аль - Бируни
Девиз урока:
Будем думать,
Будем решать,
Будем друг другу
Во всем помогать!
2) Соедините линями соответствующие части высказываний(2 мин)
| 1. Диаметр окружности – это … | | … геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. |
| 2. Дуга окружности – это … |
| … отрезок, соединяющий центр с какой-либо точкой окружности. |
| 3. Окружность – это … | … хорда, проходящая через центр окружности. |
| 4. Радиус окружности – это … |
| … отрезок, соединяющий две точки окружности. |
| 5. Хорда окружности – это … |
| … часть окружности, ограниченная двумя точками. |
Взаимопроверка
-
Освоение нового материала:
-
Осуществление учебных действий по освоению нового материала
Две окружности могут пересекаться, не пересекаться либо касаться друг друга.
Перейдем к анализу возможных случаев расположения двух окружностей.
Рассмотрим окружность с центром О1 и окружность с центром О2. Тогда расстояние между их центрами равно О1О2.
Пересекающиеся окружности имеют две общие точки.
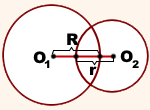
Расстояние между центрами двух пересекающихся окружностей больше разности, но меньше суммы их радиусов:
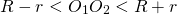 .
.
Не пересекающиеся окружности не имеет общих точек.
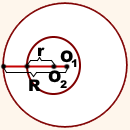
Если одна окружность лежит внутри другой, то расстояние между центрами меньше разности их радиусов:
 .
.
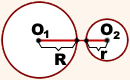
Если одна окружность находится вне другой, расстояние между центрами больше суммы их радиусов:
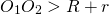 .
.
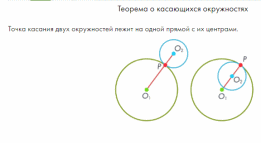
III. Касающиеся окружности имеют одну общую точку – точку касания.
При внешнем касании расстояние между центрами окружностей равно сумме их радиусов:
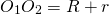 .
.
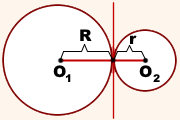
При внутреннем касании расстояние между центрами равно разности радиусов:
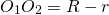 .
.
Если центры окружностей совпадают, то такие окружности называются концентрическими.
Концентрические окружности разного радиуса не пересекаются: О1О2 = 0
В случае равенства радиусов они совпадают.
Если же радиусы этих окружностей не равны, то одна из них лежит внутри другой – образуется кольцо.

Кольцом называют фигуру, заключенную между концентрическими окружностями.
Заполнить таблицу. (7 мин)
| Радиус первой окружности, см | 6 | 3 | 6 | 3 | 3 | 5 |
| Радиус второй окружности, см | 2 | 2 | 4 | 4 | 4 | 2 |
| Расстояние между центрами окружностей, см | 3 | 5 | 12 | 5 | 0 | 9 |
| Вывод о взаимном расположении
окружностей | | | | | | |
В решении задач важно подчёркивать, как расположены центры окружностей, как расположены точки касания.
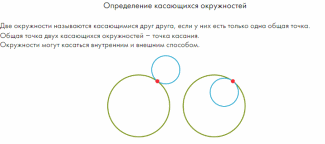
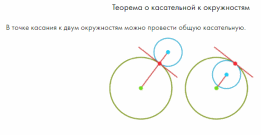

Галерея изображений (группа изображений по одной тематике)
-
-
Применение изученного материала:
-
Применение знаний, в том числе в новых ситуациях
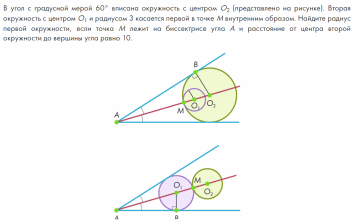
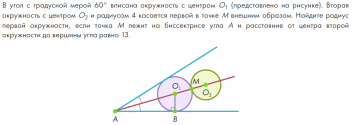
Обсудите с учащимися предложенные примеры и задачи.Задача 3 может быть резервной.
В задаче 4 необходимо обратить внимание учеников, что угол не зависит от величин радиусов касающихся окружностей.
Две окружности радиусов 4 и 9 касаются друг друга внешним образом, а также одной прямой в точках A и B. Найдите длину отрезка AB.
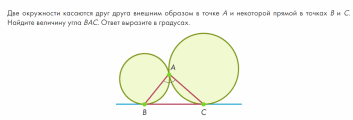
-
Выполнение заданий в формате ГИА(ОГЭ,ЕГЭ)
Предложите учащимся решить задачу самостоятельно. Расскажите учащимся решение этой задачи.
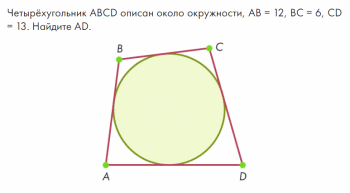
-
Подведение итогов, домашнее задание:
Подведем итогиОпределите взаимное расположение двух окружностей
1) Расстояние между центрами окружностей равно сумме их радиусов
2)Расстояние между центрами окружностей меньше суммы их радиусов.
3) Расстояние между центрами больше суммы двух радиусов.
4) Расстояние между центрами равно разности двух радиусов.
5) Расстояние между центрами окружностей равно нулю.
Предложите учащимся задачи для самостоятельного решения дома.
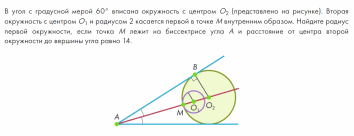

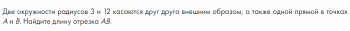
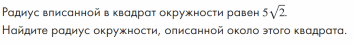

Подготовка к контрольной работе
Демоверсия
1.Отрезок BD — диаметр окружности с центром О. Хорда АС делит пополам радиус ОВ и перпендикулярна к нему. Найдите углы четырёхугольника ABCD.
2. Две противолежащие стороны четырёхугольника равны 9 см и 15 см. Чему равен периметр четырёхугольника, если в него можно вписать окружность?
3. Найдите углы четырёхугольника ABCD, вписанного в окружность, если ∠ACB = 58°, ∠ABD = 16°, ∠BAC = 44°.