Кейсы по геометрии

Кейс №3. Измерение высоты с помощью зеркала (3 ряд)

Материал к кейсу.

Вот еще один способ определения высоты дерева при помощи зеркала. На некотором расстоянии (Рис. 1) от измеряемого дерева, на ровной земле в точке С кладут горизонтально зеркальце и отходят от него назад в такую точку D, стоя в которой наблюдатель видит в зеркале верхушку А дерева. Тогда дерево (АВ) во столько раз выше роста наблюдателя (ED), во сколько раз расстояние ВС от зеркала до дерева больше расстояния CD от зеркала до наблюдателя. Почему?

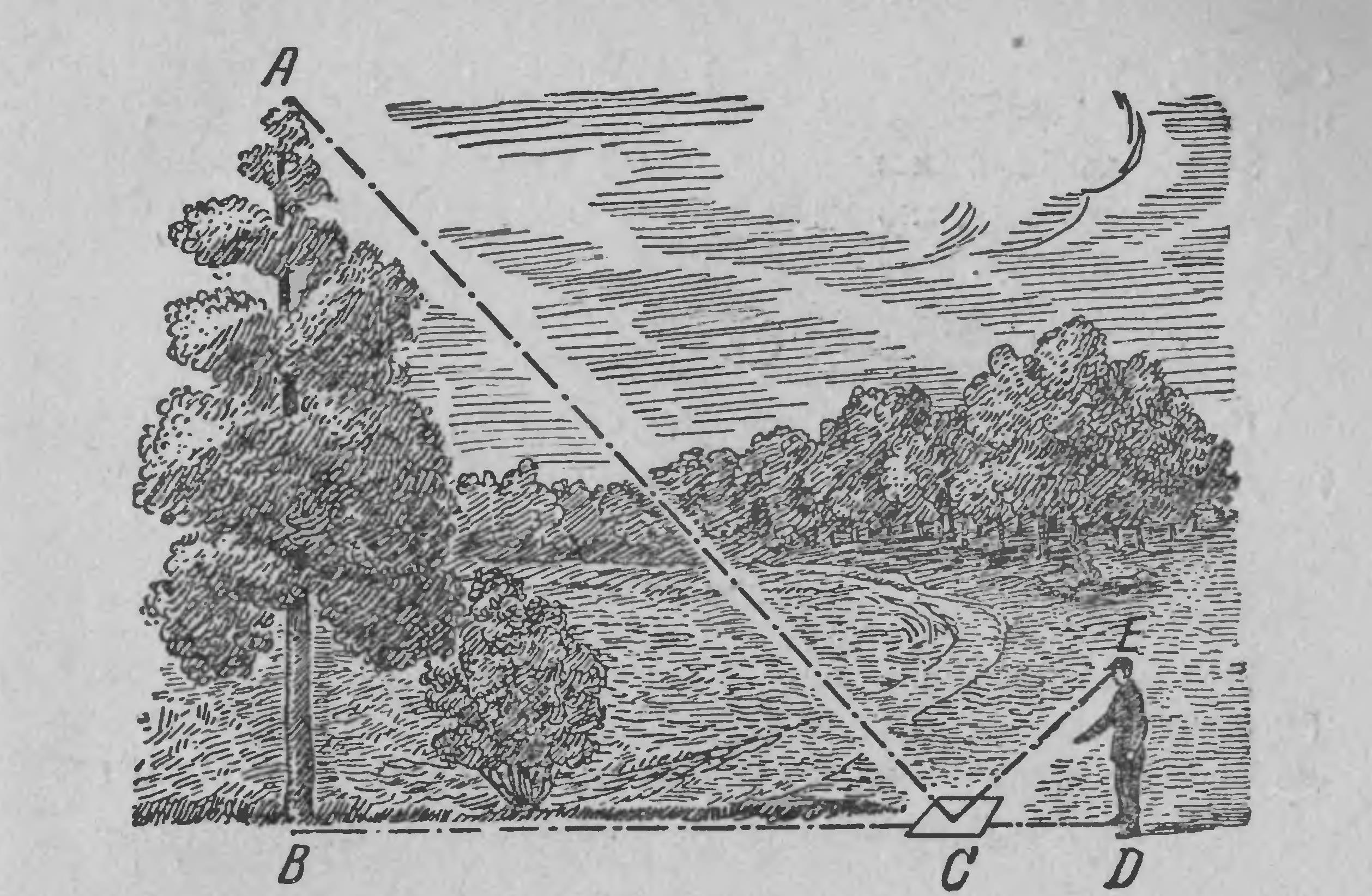
Рис.1 Измерение высоты при помощи зеркала.

Решение.

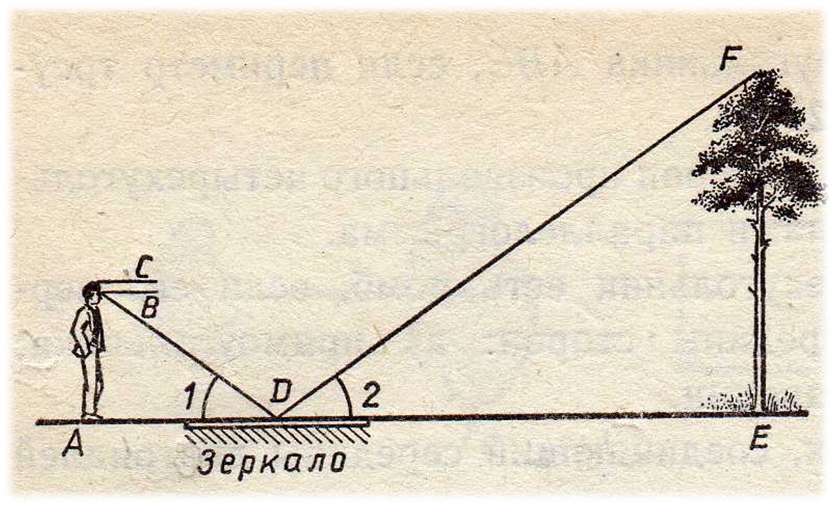
Способ основан на законе отражения света. Вершина А (Рис.2) отражается в точке А' так, что АВ = А'В. Из подобия же треугольников ВСА' и СЕВ следует, что A'B:ED = BC:CD.

В этой пропорции остается лишь заменить АʹВ равным ему АВ, чтобы обосновать указанное в задаче соотношение.

Этот удобный и нехлопотливый способ можно применять во всякую погоду, но не в густом насаждении, а к одиноко стоящему дереву.

Рис. 2 Геометрическое построение к способу измерения высоты при помощи зеркала.

Итак! Кладем зеркало на землю примерно так, как показано на фото, отходим в сторону до того момента, пока в зеркале не отразится верхушка измеряемого объекта.

Измеряем необходимые расстояния от человека до зеркала, от зеркала до столба, и получаем требуемую высоту после вычисления пропорции.

Высота столба = (рост человека * расстояние от зеркала до столба) / расстояние от человека до зеркала.

Определение высоты дерева с помощью зеркала. Задание к кейсу.

Запишите формулу для нахождения и найдите высоту дерева, если расстояние до дерева от человека 10 м, а до зеркала – 1 м.

Человек этот – один из вас.

Ответьте на вопросы:

Какие треугольники подобны и почему?

Сделайте необходимые измерения (размер головы равен размеру стопы, глаза располагаются посередине головы).

Вынесите данные на чертеж.

Чему равен коэффициент подобия?

Чему равна высота дерева?

Кейс №2. Определение высоты скалы по методу Жюля Верна. (2 ряд)

Материал к кейсу:

Отрывок из романа.

«-Сегодня нам надо измерить высоту площадки Дальней скалы, - сказал инженер.

Вам понадобится для этого инструмент? – спросил Герберт.

Нет, не понадобится. Мы будем действовать несколько иначе, обратившись к не менее простому и точному способу. Юноша, стараясь научиться, возможно, большему, последовал за инженером, который спустился с гранитной стены до окраины берега.

 Взяв прямой шест, длиной 12 футов, инженер измерил его возможно точнее, сравнивая со своим ростом, который был хорошо ему известен. Герберт нёс за ним отвес, вручённый ему инженером: просто камень, привязанный к концу верёвки. Не доходя футов 500 до гранитной стены, поднимавшейся отвесно, инженер воткнул шест фута на два в песок и, прочно укрепив его, поставил вертикально с помощью отвеса. Затем он отошёл от шеста на такое расстояние, чтобы лёжа на песке, можно было на одной прямой линии видеть и конец шеста, и край гребня. Эту точку он тщательно отметил колышком. Оба расстояния были измерены. Расстояние от колышка до палки равнялось 15 футам, а от палки до скалы 485 футам.

 «-Тебе знакомы зачатки геометрии? – спросил он Герберта, поднимаясь с земли.

-Да.

-Помнишь свойства подобных треугольников?

-Их сходственные стороны пропорциональны.

-Правильно. Так вот: сейчас я построю 2 подобных прямоугольных треугольника. У меньшего одним катетом, будет отвесный шест, другим – расстояние от колышка до основания шеста; гипотенуза же – мой луч зрения. У другого треугольника катетами будут: отвесная стена, высоту которой мы хотим определить, и расстояние от колышка до основания этой стены; гипотенуза же – мой луч зрения, совпадающий с направлением гипотенузы первого треугольника»

Задание к кейсу:

Определите высоту объекта, если высота планки 1м, расстояние от головы до планки – 2 м, а до основания скалы – 50 м.

Какие треугольники подобны и почему? Обозначьте их буквами.

Вынесите данные на чертеж.

Чему равен коэффициент подобия?

Найдите высоту скалы.

Кейс №1. Определение расстояния до объекта с помощью травинки.

(1 ряд)

Материал к кейсу. Алгоритм:

• Взять травинку подлиннее, сложить ее вдвое.

• Сложенной травинкой визуально закрыть расстояние между двумя выбранными точками, расположенными в области нужного объекта.

• Если сложенная травинка закрывает выбранный вами промежуток с излишком, то лучше оторвать лишнюю часть.

• Затем нужно развернуть травинку в длину.

• Приближайтесь к объекту, двигаясь перпендикулярно к выбранному промежутку. Время от времени следует останавливаться и смотреть на упомянутый отрезок сквозь развернутую травинку.

• Остановитесь в тот момент, когда развернутая в длину травинка полностью закроет промежуток АБ. Это значит, что человек находится на полпути от первоначального места, откуда было начато измерение.

• Измерить пройденную часть пути. Полученное значение будет равно половине расстояния до объекта. То есть пройдено и оставшееся расстояние до объекта равны.

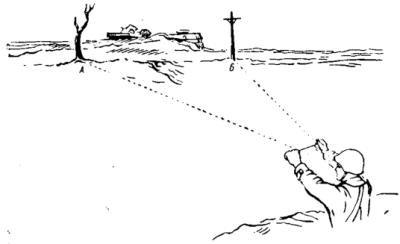
Задания к кейсу:

Введите обозначения на чертеже.

Докажите подобие треугольников.

Выполните дополнительное построение.

Выполните дополнительные измерения.

Чему равен коэффициент подобия?

Запишите формулу для нахождения расстояния.

Найдите расстояний до объекта, если вам пришлось пройти 120 шагов.