Задача (Стандартная)
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г, Д, Е. решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для букв А, Б, В, Г использовали соответственно кодовые слова 00, 01, 100, 110. Укажите кратчайшее возможное кодовое слово для буквы Д, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Примечание. Условие Фано означает, что ни одно кодовое слово не является началом другого кодового слова.
Решение:
Используем приём Дерево Фано. Расставим на этом дереве те буквы, для которых уже известны кодовые слова.
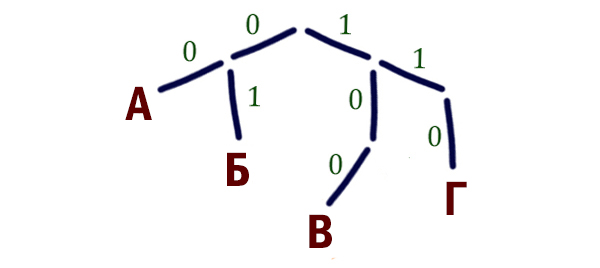
Дерево рисуется обычно сверху вниз. В начале от дерева рисуются две ветки: ветка 0 и ветка 1. От каждой ветки можно нарисовать ещё две ветки, так же 0 и 1, и т. д.
Для удобства ветки с 1 будем направлять вправо, а ветки с 0 будем направлять влево.
В конце каждой ветки можно размещать буквы, но если мы разместили букву, то эта ветка блокируется, и от этой ветки больше нельзя делать новые ответвления.
Нам осталось закодировать (расположить на дереве) две буквы: Д и Е.
Мы можем нарастить ещё две ветки от точки 1-1. Тогда получится код 111. И от точки 1-0. Тогда получится код 101.
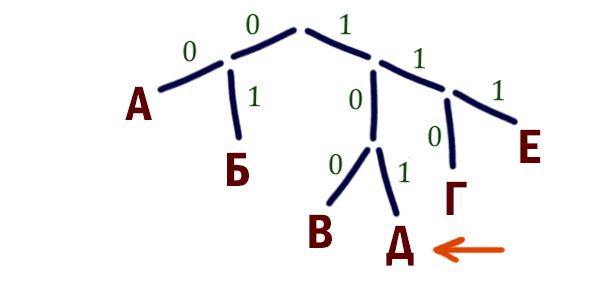
Для буквы Д нужно выбрать код с наименьшим числовым значением. Значит, для буквы Д выбираем код 101, а для буквы Е выбираем код 111.
Ответ: 101
Закрепим приём дерево Фано на ещё одной примерной задаче из ЕГЭ по информатике 2025.
Задача(Стандартная, закрепление)
Для кодирования некоторой последовательности, состоящей из букв Н, О, П, Р, С, Т, У, Ф решили использовать неравномерный двоичный код, удовлетворяющий условию, что ни одно кодовое слово не является началом другого кодового слова. Для букв Н, О, П, Р, С, Т использовали соответственно кодовые слова 10, 110, 010, 0110, 111, 0111. Укажите кратчайшее возможное кодовое слово для буквы У, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Здесь код так же должен удовлетворять Условию Фано, т.к. сказано, что ни одно кодовое слово не является началом другого кодового слова.
Значит, можем воспользоваться Деревом Фано. Расположим на Дереве Фано буквы, для которых уже известны кодовые слова.
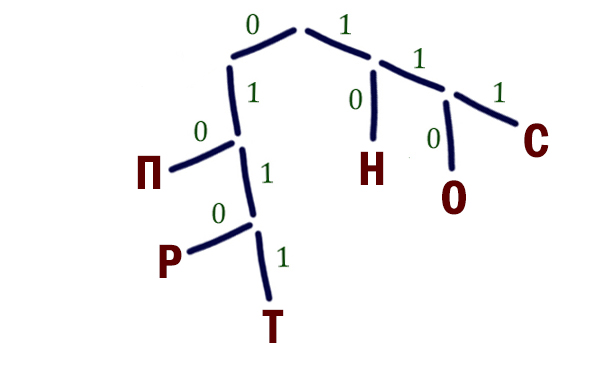
Нам нужно закодировать ещё две буквы: У, Ф. У нас единственная возможность осталась прорастить ветку от точки 0. От этой точки проращиваем ветку 0 и от этой ветки проращиваем ещё две ветки 0 и 1.
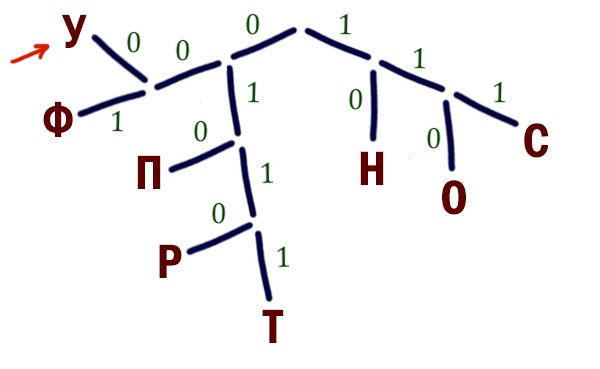
Букву У размещаем на позиции 000, потому что для этой буквы нужно выбрать код с наименьшим числовым значением.
Ответ: 000
Ещё одна примерная задача из ЕГЭ по информатике 2025 является частым гостем в различных тренировочных вариантах.
Задача (Стандартная, закрепление)
По каналу связи передаются сообщения, содержащие только семь букв: А, Б, Д, Л, Е, И, Н. Для передачи используется двоичный код, удовлетворяющий условию Фано. Кодовые слова для некоторых букв известны: А – 110, Б – 01, И – 000. Какое наименьшее количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ?
Решение:
Расставим на дереве Фано буквы, для которых известны коды.
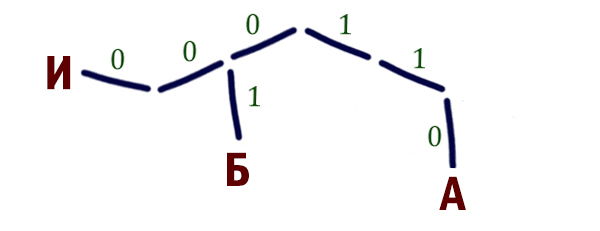
Нам осталось расположить 4 буквы: Д, Л, E, Н.
Буква Е встречается три раза в слове ДЕЛЕНИЕ, значит, ей нужно постараться присвоить самый короткий код. По дереву видно, что можно букве Е присвоить код 10.
Буквы Д, Л, Н встречаются в слове ДЕЛЕНИЕ 1 раз. Одну букву можно разместить на позицию 111. Так же можно продлить ветку из точки 00, а затем от позиции 001 сделать два отростка. У нас получатся ещё два свободных места: 0011 и 0010.
Можно оставшиеся буквы разместить следующим образом:
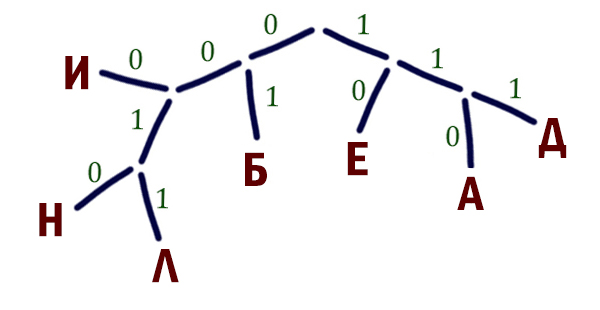
Подсчитаем какое количество двоичных знаков потребуется для кодирования слова ДЕЛЕНИЕ.

3+2+4+2+4+3+2=20
Ответ: 20
Далее решим непростую задачу из тренировочных вариантов ЕГЭ по информатике 2025. Похожая задача была в сборнике С. С. Крылова.
Задача (Непростая)
По каналу связи передаются сообщения, содержащие только четыре буквы: М, Н, Р, Т; для передачи используется двоичный код, допускающий однозначное декодирование.
Для букв М, Н, Р используются такие кодовые слова: М: 00011, Н: 1001, Р: 01100.
Укажите кратчайшее кодовое слово для буквы Т, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Нужно, чтобы код декодировался однозначно. Чтобы код декодировался однозначно, можно использовать условие Фано. Мы видим, что в уже известных кода не нарушается условие Фано. Узнаем код для буквы Т по дереву Фано. Отметим известные буквы.
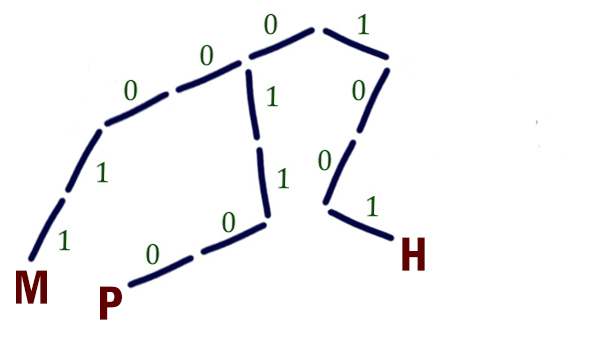
Куда разместить букву Т? Чтобы кодовое слово было кратчайшее, разместим букву Т на позицию 11.
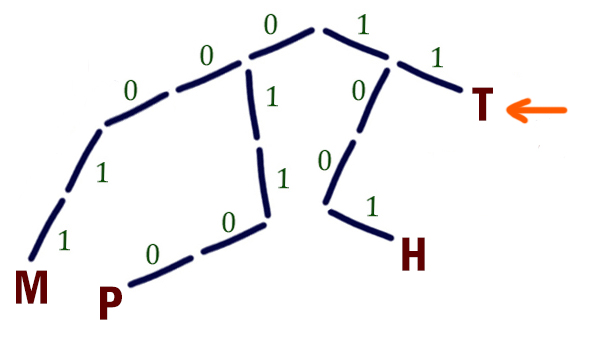
Сложность этой задачи заключается в том, что явно не указано, что нужно использовать условие Фано. Так же однозначное декодирование будет, если используется обратное условие Фано.
Обратное условие Фано: никакое кодовое слово не является окончанием другого кодового слова. Сообщения при использовании такого кода декодируются однозначно и только с конца.
Т. е. сообщения нужно такие раскодировать справа налево. Здесь про то, как будут раскодировать сообщения, ничего не сказано, поэтому мы должны проверить, какой код получится для буквы Т, если здесь используется обратное условие Фано.
Кодовое слово 0 мы использовать не можем, потому что 0 - это окончание кодового слова буквы Р. Кодовое слово 1 - это окончание кодовых слов букв М и Н. Кодовое слово 00 - это окончание кодового слова буквы Р. А вот 10 подходит для буквы Т.
Получилась следующая ситуация. Если кодовые слова будут удовлетворяют условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 11 с минимальным числовым значением. Если кодовые слова будут удовлетворяют обратному условию Фано, то для буквы Т можно написать кратчайшее кодовое слово 10 с минимальным числовым значением.
И в том и в другом случае будет однозначное декодирование. Но мы выбираем тот случай, когда кодовое слово будет наименьшим числовым значением. Таким образом, в ответе напишем 10.
Ответ: 10
Разберём ещё один нюанс в подобных задах из ЕГЭ по информатике.
Задача (Ещё раз про однозначное декодирование)
По каналу связи передаются сообщения, содержащие только четыре буквы: М, О, С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, М используются такие кодовые слова: Т: 111, О: 0, М: 100. Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
Решение:
Здесь условие похоже на то, которое было в предыдущей задаче. Но обратное условие Фано здесь не применимо, т.к. код для буквы О является окончанием для кода буквы М.
Значит, у нас остаётся единственный инструмент, чтобы сообщения декодировались однозначно - это условие Фано. Теперь задачу решаем как обычно по дереву Фано.
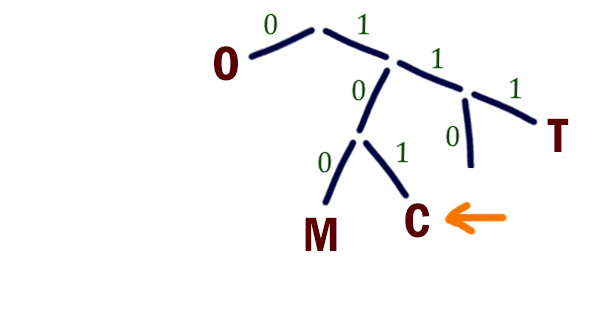
Выбираем из двух вариантов: 110 и 101. Но останавливаемся на 101, т.к. это кодовое слово с наименьшим числовым значением.
Ответ: 101
Решим задачу, которая часто встречается в бумажных сборниках по подготовке к ЕГЭ по информатике.
Задача (код не удовлетворяет условию Фано)
По каналу связи передаются шифрованные сообщения, содержащие только пять латинских букв: A, B, С, D, E. Для передачи используется неравномерный двоичный код. Для некоторых букв известны кодовые слова: A: 01, B: 10, C: 11, D: 000.
Укажите самое короткое кодовое слово для буквы E, при котором код не будет удовлетворять условию Фано, при этом в записи самого этого слова должно использоваться более одного символа, а само слово не должно совпадать ни с одним из используемых слов для букв с известными кодами.
Если таких слов несколько, то укажите слово с наименьшим числовым значением.
Решение:
Здесь код не должен однозначно декодироваться.
Подходит код 00, т.к. длина этого кодового слова больше чем 1 символ. Этот код не совпадает ни с одним кодом для известных букв. Этот код нарушает принцип условия Фано, видно, что он является началом кодового слова буквы D. И этот код имеет самое маленькое числовое значение.
Ответ: 00
В 4 задании из ЕГЭ по информатике 2025 не обязательно может попасться задача, связанная с условием Фано. Может просто быть задача на кодирование и декодирование информации.
Задача (Заключительная)
По заданной системе кодирования, буквам X, К, Л, О и Д соответствуют двоичное представление чисел 0, 1, 2, 3 и 4 соответственно (с сохранением одного незначащего нуля в случае одноразрядного представления). Примените указанный метод кодирования к последовательности букв ХОЛОДОК и запишите результат в формате шестнадцатеричного кода.
Решение:
Распишем, как кодируются все буквы в двоичной системе. Ноль и один кодируются одним разрядом, поэтому к ним слева приписывается ноль, как написано в условии.
| Буква | Десятичное Представление | Двоичное Представление |
| Х | 0 | 00 |
| К | 1 | 01 |
| Л | 2 | 10 |
| О | 3 | 11 |
| Д | 4 | 100 |
Выписываем слово ХОЛОДОК и под ним кодовые слова букв.

Чтобы перевести из двоичной системы число в шестнадцатеричную систему, мы должны двоичные цифры разбить по четвёркам, начиная с правого края. Каждая четвёрка превращается в цифру в шестнадцатеричной системе. Таблицу перевода четвёрок двоичных цифр в шестнадцатеричную систему можно посмотреть в этой статье.
Т.к. ЕГЭ по информатике сдаётся в компьютерной форме, то можно воспользоваться стандартным калькулятором в режиме программист.
Ответ: 1DCD



























