Колебательный контур. Свободные и вынужденные колебания. Резонанс.
Электрические и магнитные явления тесно связаны друг с другом. Простейшей системой, где это можно наблюдать, является колебательный контур - цепь, состоящая из катушки индуктивности L и конденсатора С.
Е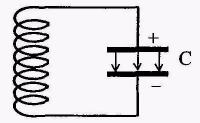 сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора
сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора  (где q – заряд на пластинах конденсатора) будет превращаться в энергию магнитного поля катушки
(где q – заряд на пластинах конденсатора) будет превращаться в энергию магнитного поля катушки 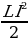 . Когда
. Когда
Рис. 15.1 конденсатор полностью разрядится, ток в катушке и связанная с ним энергия
магнитного поля достигнут максимума. Ток будет некоторое время поддерживаться за счет ЭДС самоиндукции, пока конденсатор не перезарядится. Энергия магнитного поля катушки преобразуется в энергию электрического поля перезаряженного конденсатора. Конденсатор снова начнет разряжаться, и явления повторятся в обратной последовательности. За время Т в контуре восстановится исходное состояние. Возникают периодические электрические колебания, сопровождающиеся превращением электрической энергии в магнитную и обратно.
Колебания с периодом Т испытывают заряд q на обкладках конденсатора, разность потенциалов между ними, сила тока в контуре, напряженность электрического поля конденсатора и индукция магнитного поля катушки.
Составим уравнение колебаний, например, заряда на обкладках конденсатора и определим период этих колебаний. Примем, что сопротивление R контура очень мало и потерями энергии в контуре можно пренебречь. При этом полная энергия электрического и магнитного полей с течением времени не изменяется:
 . (15.1)
. (15.1)
После преобразований получим дифференциальное уравнение собственных колебаний:
 (15.2)
(15.2)
Электрические колебания, происходящие в колебательном контуре без воздействия внешних ЭДС, получили название собственных или свободных электрических колебаний.
Введя обозначения 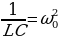 , приходим к следующей записи:
, приходим к следующей записи:
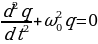 (15.3)
(15.3)
где ω0 — собственная частота контура. Получили уравнение колебаний заряда q на обкладках конденсатора. Решение уравнения (15.3) имеет вид:
q = q0cos(ω0t + φ), (15.4)
где q0 - амплитудное значение заряда, ω0 – циклическая частота собственных колебаний, φ – фаза колебаний. Дифференциальное уравнение (15.3) не отличается от уравнения колебаний гармонического осциллятора:
 (15.5)
(15.5)
где х – смещение точки от положения равновесия.
Заряд q и все перечисленные выше электрические величины будут гармонически (по закону синуса или косинуса) изменяться в колебательном контуре во времени с частотой 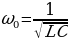 , а период этих колебаний определяется формулой Томсона:
, а период этих колебаний определяется формулой Томсона:
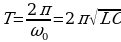 (15.6)
(15.6)
Напряжение на конденсаторе отличается от заряда множителем 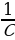 :
:
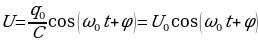 . (15.7)
. (15.7)
Продифференцировав выражение (15.4) по времени, получим выражение для силы тока:
 . (15.8)
. (15.8)
Таким образом, сила тока опережает по фазе напряжение на конденсаторе на 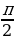 .
.
Из выражений (15.7) и (15.8) следует, что  ,
, 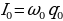 . Используя выражение
. Используя выражение 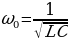 , получим
, получим 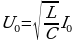 . (15.9)
. (15.9)
В реальном колебательном контуре (R ≠ 0) свободные электромагнитные колебания являются затухающими. Уравнение колебаний в данном контуре будет:
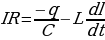 . (15.10)
. (15.10)
Дифференциальное уравнение затухающих колебаний:
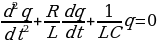 . (15.11)
. (15.11)
Приняв во внимание, что 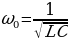 и введя обозначения
и введя обозначения  (β коэффициент затухания), получим выражение (15.11) в виде:
(β коэффициент затухания), получим выражение (15.11) в виде:
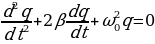 (15.12)
(15.12)
При условии, что β2 ω02 , то есть 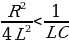 , решение уравнения (15.12) имеет вид:
, решение уравнения (15.12) имеет вид:
q = q0e-βtcos (ωt + φ), (15.13)
где  . Подставив значения
. Подставив значения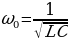 и
и  , получим, что
, получим, что
 . (15.14)
. (15.14)
Таким образом, частота затухающих колебаний ω меньше собственной частоты ω0
Разделив функцию (15.13) на емкость С, получим напряжение на конденсаторе:
 . (15.15)
. (15.15)
Чтобы найти силу тока I, продифференцируем выражение (15.13) по времени:
I = q0e-βt[-β cos(ωt+φ) - ω sin(ωt+φ)]. (15.16)
произведя преобразования (15.16), получим
I = I0e-βt cos(ωt+φ+α). (15.17)
так как coaα , а sinα 0, то значение а заключено в пределах от 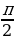 до π.
до π.
Таким образом, при наличии в контуре активного сопротивления R сила тока опережает по фазе напряжение на конденсаторе более чем на 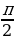 (при R = О опережение составляет
(при R = О опережение составляет 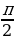 ).
).
Кроме коэффициента β для характеристики затухающих колебаний пользуются логарифмическим декрементом затухания δ, который равен натуральному логарифму отношения амплитуд колебаний, взятых через период Т:
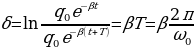 . (15.18)
. (15.18)
Величина  определяет число периодов, за которое амплитуда колебаний убывает в е раз.
определяет число периодов, за которое амплитуда колебаний убывает в е раз.
Чтобы вызвать вынужденные колебания, нужно оказывать на систему внешнее периодически изменяющееся воздействие. В случае электрических колебаний нужно включить последовательно с элементами контура переменную ЭДС или, разорвав контур, подать на образовавшиеся контакты переменное напряжение U = U0cosωt
Для контура (рис. 15.2) можем записать 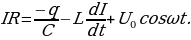 (15.20)
(15.20)
Произведя преобразования, получим дифференциальное уравнение вынужденных колебаний:
 (15.21)
(15.21)
где  ,
, 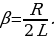
Решение уравнения (15.21) имеет вид
q = q0cos(ωt-ψ) , (15.22)
где ψ – начальная фаза,

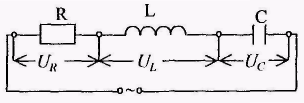 (15.23)
(15.23)
 . (15.24)
. (15.24)
Рис. 15.2
Продифференцировав выражение (15.22) по t, найдем силу тока I в контуре:
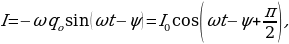
или
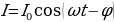 , (15.25)
, (15.25)
где  есть сдвиг по фазе между током и напряжением, тогда
есть сдвиг по фазе между током и напряжением, тогда
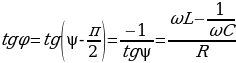 (15.26)
(15.26)
Из выражения (15.26) следует, что ток отстает по фазе от напряжения 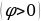 в том случае, когда
в том случае, когда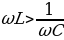 , и опережает напряжение
, и опережает напряжение 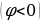 при условии, что
при условии, что 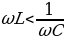 .
.
Согласно выражения (15.23)  (15.27)
(15.27)
Представим соотношение (15.20) в виде  (15.28)
(15.28)
Произведение IR равно напряжению на активном сопротивлении 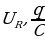 - напряжение на конденсаторе
- напряжение на конденсаторе 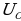 , выражение
, выражение 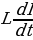 определяет напряжение на индуктивности
определяет напряжение на индуктивности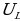 . С учетом этого можно записать
. С учетом этого можно записать 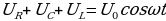 (15.29)
(15.29)
Сумма напряжений на отдельных элементах контура в каждый момент времени равна напряжению, приложенному извне.
В соответствии с (15.25) напряжение на активном сопротивлении 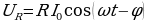 (15 30)
(15 30)
Разделив выражение (15.22) на емкость, получим напряжение на конденсаторе:
 (15.31)
(15.31)
 (15.32)
(15.32)
 .
.
Умножив производную функцию (15.25) на L, получим напряжение на индуктивности:
 (15.33)
(15.33)  (15.34)
(15.34) 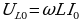
Сопоставление выражений (15.25), (15.30), (15.31) и (15.33) показывает, что напряжение на емкости отстает по фазе от силы тока на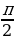 , а напряжение на индуктивности опережает ток на
, а напряжение на индуктивности опережает ток на 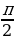 . Напряжение на активном сопротивлении изменяется в фазе с током.
. Напряжение на активном сопротивлении изменяется в фазе с током.
Установившиеся вынужденные электрические колебания происходят с частотой, равной частоте внешней вынуждающей силы, независимо от величины параметров самой колеблющейся системы, то есть независимо от R, L, С. Этим объясняется, что в цепях переменного тока колебания тока I (или заряда q на конденсаторе) всегда происходят с частотой ЭДС генератора, независимо от того, какова эта цепь. Амплитуда же колебаний и сдвиг фаз, наоборот, существенно зависят от параметров цепи.
Электрической автоколебательной системой является ламповый генератор незатухающих электрических колебаний.
В реальном контуре 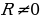 из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
Колебательный контур включен в анодную цепь лампы. При ее замыкании конденсатор заряжается и в контуре возбуждаются свободные колебания. Протекающий по катушке переменный ток наводит в связанной с ней индуктивно катушке обратной связи - переменную ЭДС. Переменное напряжение с этой катушки поступает на промежуток сетка-катод. Изменения сеточного напряжения вызывают изменения анодного тока с частотой, равной частоте 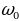 свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
При последовательном соединении активного сопротивления R, реактивных сопротивлений (индуктивного L и ёмкостного С) в цепи действует переменная ЭДС, изменяющаяся по закону
ε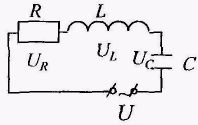 = ε0sinωt и I=I0sinωt . При изменении частоты ω изменяется амплитуда тока I и сдвиг фаз φ. При частоте ω = ω0, определяемой условием
= ε0sinωt и I=I0sinωt . При изменении частоты ω изменяется амплитуда тока I и сдвиг фаз φ. При частоте ω = ω0, определяемой условием  , реактивное сопротивление
, реактивное сопротивление  обращается в нуль в законе Ома
обращается в нуль в законе Ома
 , сила тока I при этом достигает максимального значения
, сила тока I при этом достигает максимального значения
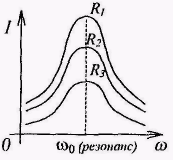 Рис 14.10
Рис 14.10 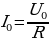 , контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ. Такой резонанс называется резонансом напряжений.
, контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ. Такой резонанс называется резонансом напряжений.
Рис. 14.11

Рис. 14.12
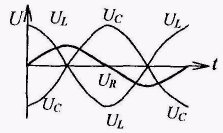 Напряжение на L и С сдвинуты по фазе на 180°, т.е. компенсируют друг друга (рис. 14.13). При параллельном соединении L и С, при соотношении
Напряжение на L и С сдвинуты по фазе на 180°, т.е. компенсируют друг друга (рис. 14.13). При параллельном соединении L и С, при соотношении  , сдвиг фаз φ становится равным нулю и, следовательно, контур ведет себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвленной цепи называется резонансом токов
, сдвиг фаз φ становится равным нулю и, следовательно, контур ведет себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвленной цепи называется резонансом токов
Рис. 14.13 (рис. 14.14). Оба тока IL и IC обладают разностью фаз близкой к 180°, т.е. находятся в противофазах. При резонансе полный ток становится наименьшим, а сопротивление контура достигает наибольшего значения 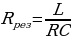 . При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
. При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
Р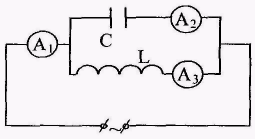 езонанс напряжений широко используется в радиотехнике для выделения из многих сигналов различных радиостанций только одной частоты (настроиться на одну частоту). Вредное влияние резонанса в электрических цепях проявляется в тех случаях, когда в цепи возникают большие токи или напряжения (когда цепи не предусмотрены на работу в условиях резонанса), происходит расплавление проводов, пробой
езонанс напряжений широко используется в радиотехнике для выделения из многих сигналов различных радиостанций только одной частоты (настроиться на одну частоту). Вредное влияние резонанса в электрических цепях проявляется в тех случаях, когда в цепи возникают большие токи или напряжения (когда цепи не предусмотрены на работу в условиях резонанса), происходит расплавление проводов, пробой
Рис. 14.14 изоляции и т.д.







 сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора
сли обкладки заряженного конденсатора соединить с концами катушки, конденсатор будет разряжаться и в контуре появится ток I. Энергия электрического поля конденсатора  (где q – заряд на пластинах конденсатора) будет превращаться в энергию магнитного поля катушки
(где q – заряд на пластинах конденсатора) будет превращаться в энергию магнитного поля катушки 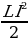 . Когда
. Когда  . (15.1)
. (15.1) (15.2)
(15.2)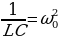 , приходим к следующей записи:
, приходим к следующей записи: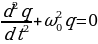 (15.3)
(15.3) (15.5)
(15.5)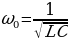 , а период этих колебаний определяется формулой Томсона:
, а период этих колебаний определяется формулой Томсона: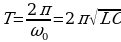 (15.6)
(15.6)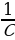 :
: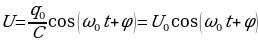 . (15.7)
. (15.7) . (15.8)
. (15.8)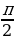 .
. ,
, 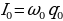 . Используя выражение
. Используя выражение 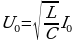 . (15.9)
. (15.9)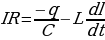 . (15.10)
. (15.10)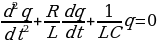 . (15.11)
. (15.11) (β коэффициент затухания), получим выражение (15.11) в виде:
(β коэффициент затухания), получим выражение (15.11) в виде: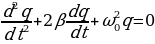 (15.12)
(15.12)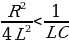 , решение уравнения (15.12) имеет вид:
, решение уравнения (15.12) имеет вид: . Подставив значения
. Подставив значения . (15.14)
. (15.14) . (15.15)
. (15.15)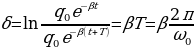 . (15.18)
. (15.18) определяет число периодов, за которое амплитуда колебаний убывает в е раз.
определяет число периодов, за которое амплитуда колебаний убывает в е раз.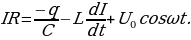 (15.20)
(15.20) (15.21)
(15.21) ,
, 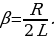

 (15.23)
(15.23) . (15.24)
. (15.24)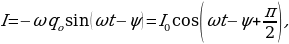
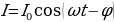 , (15.25)
, (15.25) есть сдвиг по фазе между током и напряжением, тогда
есть сдвиг по фазе между током и напряжением, тогда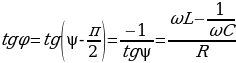 (15.26)
(15.26)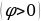 в том случае, когда
в том случае, когда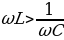 , и опережает напряжение
, и опережает напряжение 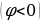 при условии, что
при условии, что 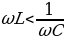 .
. (15.27)
(15.27) (15.28)
(15.28)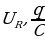 - напряжение на конденсаторе
- напряжение на конденсаторе 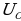 , выражение
, выражение 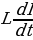 определяет напряжение на индуктивности
определяет напряжение на индуктивности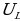 . С учетом этого можно записать
. С учетом этого можно записать 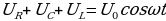 (15.29)
(15.29)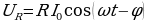 (15 30)
(15 30) (15.31)
(15.31) (15.32)
(15.32) .
. (15.33)
(15.33)  (15.34)
(15.34) 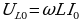
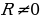 из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.
из-за потерь энергии (джоулево тепло, излучение) колебания со временем затухают. Их можно поддерживать, пополняя энергию контура извне. На этом основано действие лампового генератора.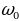 свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода.
свободных колебаний в контуре. Если фаза колебаний анодного тока согласована (совпадает) с фазой колебаний в контуре, то энергия колебательного контура будет пополняться за счет энергии батареи и, таким образом, в контуре будут поддерживаться незатухающие колебания. Поступление энергии от источника регулируется самим контуром. Если присоединить электрическую цепь лампового генератора к входу электронного осциллографа, то при замыкании ключа на экране видны незатухающие электромагнитные колебания. Периодическое изменение силы анодного тока достигается периодическим изменением потенциала сетки триода. = ε0sinωt и I=I0sinωt . При изменении частоты ω изменяется амплитуда тока I и сдвиг фаз φ. При частоте ω = ω0, определяемой условием
= ε0sinωt и I=I0sinωt . При изменении частоты ω изменяется амплитуда тока I и сдвиг фаз φ. При частоте ω = ω0, определяемой условием  обращается в нуль в законе Ома
обращается в нуль в законе Ома , сила тока I при этом достигает максимального значения
, сила тока I при этом достигает максимального значения Рис 14.10
Рис 14.10 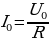 , контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ. Такой резонанс называется резонансом напряжений.
, контур действует как чисто активное сопротивление. Полное сопротивление равно наименьшему значению. Чем меньше сопротивление R1R2R3, тем более острый максимум имеет кривая (рис. 14.11). Ток I при резонансе совпадает по фазе с напряжением U. Сдвиг фаз между током и напряжением φ = 0 . При последовательном соединении в момент резонанса UL = UC . Напряжение на зажимах равно активному UR =Uобщ. Такой резонанс называется резонансом напряжений.
 Напряжение на L и С сдвинуты по фазе на 180°, т.е. компенсируют друг друга (рис. 14.13). При параллельном соединении L и С, при соотношении
Напряжение на L и С сдвинуты по фазе на 180°, т.е. компенсируют друг друга (рис. 14.13). При параллельном соединении L и С, при соотношении  , сдвиг фаз φ становится равным нулю и, следовательно, контур ведет себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвленной цепи называется резонансом токов
, сдвиг фаз φ становится равным нулю и, следовательно, контур ведет себя как чисто активное сопротивление. Этот частный случай вынужденных колебаний в разветвленной цепи называется резонансом токов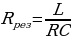 . При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей.
. При резонансе токов амперметр А1 показывает на много меньший ток, чем амперметры А2 и А3, это обстоятельство используют при устройстве индукционных печей. езонанс напряжений широко используется в радиотехнике для выделения из многих сигналов различных радиостанций только одной частоты (настроиться на одну частоту). Вредное влияние резонанса в электрических цепях проявляется в тех случаях, когда в цепи возникают большие токи или напряжения (когда цепи не предусмотрены на работу в условиях резонанса), происходит расплавление проводов, пробой
езонанс напряжений широко используется в радиотехнике для выделения из многих сигналов различных радиостанций только одной частоты (настроиться на одну частоту). Вредное влияние резонанса в электрических цепях проявляется в тех случаях, когда в цепи возникают большие токи или напряжения (когда цепи не предусмотрены на работу в условиях резонанса), происходит расплавление проводов, пробой









