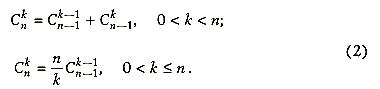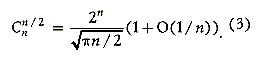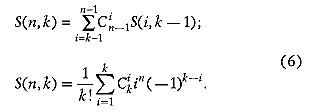Комбинаторные задачи на программирование
С учениками на уроках информатики мы сталкиваемся с задачами, где нужно найти количество комбинаций чего-либо. Начинаем всегда с самой простой задачи, когда надо найти и вывести на экран все комбинации произведений однозначных чисел, то есть таблицу умножения (для этого достаточно хорошо понимать вложенные циклы):
…
for i:=2 to 9 do
for j:=2 to 9 do
writeln(i,’ * ‘,j,’ = ‘,i*j);
…
или изменим параметр вложенного цикла и получим вывод комбинаций без повторений:
…
for i:=2 to 9 do
for j:=i to 9 do
writeln(i,’ * ‘,j,’ = ‘,i*j);
…
Уже из первого примера понятно, что найти количество комбинаций и вывести их на экран – это не одно и тоже.
К моменту изучения вложенных циклов и перебора с таблицей умножения мои ученики уже знают, стандартный алгоритм и программу нахождения факториала:
…
read(n);
p:=1;
for i:=1 to n do
p:=p*i;
writeln(’n! = ‘,p);
…
Поэтому найти количество перестановок, размещений, сочетаний найти не сложно, надо только знать формулы из комбинаторики, которые рассмотрим ниже и немного подумать какую формулу в данной задаче применить.
а) перестановки без повторений - комбинаторные соединения, которые могут отличаться друг от друга лишь порядком входящих в них элементов p=n!
Пример: из цифр 1,2,3 можно составить p=3!=1*2*3=6 комбинаций
123, 132, 213, 231, 312, 321.
б) перестановки с повторениями комбинаторные соединения, в которых среди образующих элементов имеются одинаковые p=n!/(m1!*m2!*…)
Пример: из 3 цифр 1,1,2 – две единицы p=3!/(2!*1!)=6/2=3
11, 12, 22
в) Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке. . p=m!/(m-n)!
Пример: из 4 цифр 0,1,2,3 составим размещения без повторений из 2-х цифр p=4!/(4-2)!=24/2=12
01, 02, 03, 10, 12, 13, 20, 21, 23, 30, 31, 32
Примером из жизни может быть количество игр проводимых футболистами в группе на чемпионате страны (в 2 круга).
г) Размещения с повторениями — комбинаторные соединения, составленные из n элементов по m. При этом каждый из n элементов может содержаться сколько угодно раз или вообще отсутствовать. p=nm (формула получена путем убывающего факториала см. Википедия)
Пример: составим комбинации (размещения) из 2 цифр длиной 8 цифр – 28=256,
00000000, 00000001, …, 11111110, 11111111 (наверное, вспомнили ребята, где применяется эта формула в информатике)
Примером из жизни может быть количество символов в алфавите или палитра изображения при кодировании текстовой или графической информации определенных количеством бит (длина кода).
д) Сочетания без повторений — комбинаторные соединения из n элементов по m, составленные из этих элементов и отличающиеся друг от друга только составом. p=m!/(m-n)!n!
Пример: из 4 цифр 0,1,2,3 составим сочетания без повторений из 2-х цифр p=4!/(4-2)!2!=24/4=6
01, 02, 03, 12, 13, 23
Примером из жизни может быть количество игр проводимых футболистами в группе на чемпионате мира.
е) Сочетания с повторениями — комбинаторные соединения из n элементов по m, составленные из этих элементов без учета порядка с возможностью многократного повторения предметов. p=(n+m-1)!/m!(n-1)!
Пример: из 4 цифр 0,1,2,3 составим сочетания с повторениями из 2-х цифр p=(4+2-1)!/4!(2-1)!=120/12=10
00, 01, 02, 03, 11, 12, 13, 22, 23, 33
Примером из жизни может быть количество молекул составленных из 2-х атомов, причем имеются атомы 4-х видов.
А как сделать вывод всех комбинаций (в вышеописанных ситуациях)? Здесь формулы не нужны, а всё можно сделать вложенными циклами (по крайней мере, для простых школьных задач). Мы меняем параметр и получаем все вышеописанные ситуации (ниже рассмотрим несколько примеров):
Задача 1. ДЕМО-программа показывает 4 вида комбинаций
program kombin;
const n=4;
var a:array[1..n] of integer; b:array[1..n] of string;
i,j:integer; q,w:byte;
begin
for i:=1 to n do a[i]:=i-1; w:=64; for i:=1 to n do b[i]:=chr(w+i);
writeln('Выберите, что хотите получить:');
writeln('1:размещения с повторениями');
writeln('2:размещения без повторений');
writeln('3:сочетания с повторениями');
writeln('4:сочетания без повторений');
readln(q);
case q of
1:for i:=1 to n do
for j:=1 to n do begin write(a[i],a[j],' '); writeln(b[i],b[j]); end;
2:for i:=1 to n do
for j:=1 to n do if ij then begin write(a[i],a[j],' '); writeln(b[i],b[j]); end;
3:for i:=1 to n do
for j:=i to n do begin write(a[i],a[j],' '); writeln(b[i],b[j]); end;
4:for i:=1 to n-1 do
for j:=i+1 to n do begin write(a[i],a[j],' '); writeln(b[i],b[j]); end;
end;
readln;
end.
Задача 2. Сколькими способами можно набрать n рублей, если существуют монеты 1, 2, 5, 10 и 50 рублей.
var n,i,j,k,l,m,s:byte;
begin
readln(n);
for i:=0 to n do
for j:=0 to n div 2 do
for k:=0 to n div 5 do
for l:=0 to n div 10 do
for m:=0 to n div 50 do
if i+j*2+k*5+l*10+m*50=n then begin
writeln('1*',i,'+2*',j,'+5*',k,'+10*',l,'+50*',m,'=',n);
s:=s+1; end;
writeln('Комбинаций ',s);
readln;
end.
Задача 3.Сколько можно составить слов из 4 букв, при этом алфавит состоит из 20 букв
const n=20;
a:array[1..n] of string=('а','б','в','г','д','е','ж','з','и','к',
'л','м','н','о','п','р','с','т','у','ф');
var i,j,k,l:integer; s:real;
begin
for i:=1 to n-3 do
for j:=i+1 to n-2 do
for k:=j+1 to n-1 do
for l:=k+1 to n do begin
writeln(a[i]:2,a[j]:2,a[k]:2,a[l]:2);
s:=s+1;
end;
writeln(s*s*s*s:20:0);
readln;
end.
Вывод: Знания основ комбинаторики и умение их применять в программировании позволяет решить множество задач из математики, информатики и просто задач из повседневной жизни, с которыми мы сталкиваемся.
Литература:
-
Лисичкин В. Т., Соловейчик И. Л. Математика — Москва: Высшая школа, 1991. — 480 c.
-
Википедия
-
Вы - -й посетитель этой странички
-
Олимпиады по информатике. Пути к вершине
-
Лекции читает Е.В. Андреева
-
Лекция 6. Комбинаторные задачи
-
Задачи дискретной математики, к которым относится большинство олимпиадных задач по информатике, часто сводятся к перебору различных комбинаторных конфигураций объектов и выбору среди них наилучшего, с точки зрения условия той или иной задачи. Поэтому знание алгоритмов генерации наиболее распространенных комбинаторных конфигураций является необходимым условием успешного решения олимпиадных задач в целом. Важно также знать количество различных вариантов длякаждого типа комбинаторных конфигураций, так как этопозволяет реально оценить вычислительную трудоемкость выбранного алгоритма решения той или иной задачи наперебор вариантов и, соответственно, его приемлемость для решения рассматриваемой задачи, с учетом ее размерности. Кроме того, при решении задач полезным оказывается умение для каждой из комбинаторных конфигураций выполнять следующие операции: по имеющейся конфигурации получать следующую за ней в лексикографическом порядке; определять номер данной конфигурации в лексикографической нумерации всех конфигураций; и, наоборот, по порядковому номеру выписывать соответствующую ему конфигурацию.
-
Перечисленные подзадачи в программировании обычно рассматривают для следующих комбинаторных конфигураций: перестановки элементов множества, подмножества множества, сочетания из n элементов множества по k элементов ( k-элементные подмножества мно-жества, состоящего из n 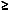 k элементов), размещения (упорядоченные подмножества множества, то есть отличающиеся не только составом элементов, но и порядком элементов в них), разбиения множества (множество разбивается на подмножества произвольного размера так, что каждый элемент исходного множества содержится ровно в одном подмножестве), разбиения натуральных чисел на слагаемые, правильные скобочные последовательности (различные правильные взаимные расположения пар открывающихся и закрывающихся скобок).
k элементов), размещения (упорядоченные подмножества множества, то есть отличающиеся не только составом элементов, но и порядком элементов в них), разбиения множества (множество разбивается на подмножества произвольного размера так, что каждый элемент исходного множества содержится ровно в одном подмножестве), разбиения натуральных чисел на слагаемые, правильные скобочные последовательности (различные правильные взаимные расположения пар открывающихся и закрывающихся скобок).
-
Большинство указанных конфигураций были подробно рассмотрены в [1—3]. Однако при генерации различных конфигураций использовались в основном нерекурсивные алгоритмы.Опытные же участники олимпиад в подобных случаях при программировании используют в основном именно рекурсию, с помощью которой решение рассматриваемых задач зачастую можно записать более кратко и прозрачно. Поэтому для полноты изложения данной темы приведем ряд рекурсивных комбинаторных алгоритмов и рассмотрим особенности применения рекурсии в комбинаторике.
-
Генерация k -элементных подмножеств
-
В комбинаторике такие подмножества называют сочетаниями из n элементов по k элементов и обозначают 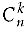 .
.
-
Их количество выражается следующей формулой:
-
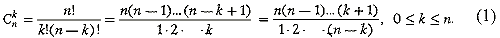
-
Однако при программировании гораздо удобнее использовать следующие рекуррентные соотношения:
-
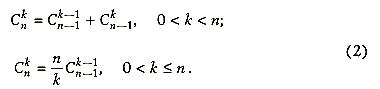
-
Объясняется это тем, что в формуле (1) числитель и знаменатель растут очень быстро, поэтому в силу особенностей компьютерной арифметики не всегда возможно точно вычислить значение 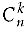 , даже когда последнеене превосходит максимально представимое целое число.
, даже когда последнеене превосходит максимально представимое целое число.
-
При фиксированном значении n максимального значения число сочетаний достигает при k = n/2 (вернее,для четного n максимум один, и он указан, а для нечетного — максимум достигается на двух соседних значениях k: [n/2] и [n/2] + 1). Поэтому особенно полезной оказывается следующая оценка для четных n [4] (очевидно, что при нечетных n отличия будут минимальными), основанная на формуле Стирлинга:
-
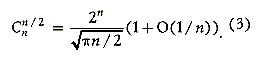
-
Если допустить, что за время, отведенное для решения задачи, мы можем перебрать около 10 6 вариантов, то из формулы (3) следует, что генерацию всех сочетаний из n элементов для любого фиксированного k можнопроводить для n 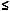 24.
24.
-
Обычно генерацию всех k-элементных подмножеств проводят в лексикографическом порядке, тем более чтов данном случае это не приводит ни к усложнению алгоритма, ни к увеличению его вычислительной трудоемкости. Напомним, что порядок подмножеств называется лексикографическим, если для любых двух подмножеств справедливо, что раньше должно быть сгенерировано тоиз них, из индексов элементов которого можно составить меньшее k-значное число в n-ричной системе счисления (или в десятичной, для n n = 6 иk = 3 сочетание из третьего, первого и пятого элементов должно быть сгенерировано раньше, чем из второго, третьего и четвертого, так как 135
-
Рассмотрим рекурсивный алгоритм решения данной задачи. Идея сведения данной задачи к задаче меньшей размерности следующая. Первым элементом подмножества может быть любой элемент, начиная с первого и заканчивая (n — k + 1)-м элементом. После того, как индекс первого элемента подмножества зафиксирован, осталось выбрать k — 1 элемент из элементов с индексами большими, чем у первого. Далее поступаем аналогично. Когда выбран последний элемент, то мы достигли конечного уровня рекурсии и выбранное подмножество можно обработать (проанализировать или распечатать). В предлагаемой ниже программе массив a содержит значения элементов исходного множества и может быть заполнен произвольным образом. В массиве p будем формировать очередное сочетание изk элементов.
-
const nmax = 24;
type list = array[1..nmax] of integer;
var k, i, j, n, q: integer;
a, p: list;
procedure print(k: integer);
var i: integer;
begin
for j := 1 to k do
write(p[j]:4);
writeln
end;{print}
-
procedure cnk(n, k: integer);
procedure gen(m, L: integer);
var i: integer;
begin
if m = 0 then print(k)
else
for i := L to n — m + 1 do
begin
p[k — m + 1] := a[i];
gen(m — 1, i + 1)
end
end;{gen}
-
begin {cnk}
gen(k, 1)
end;{cnk}
begin {main}
readln(n,k);
for i := 1 to n do
a[i] := i;
{заполнить массив можно и по-другому}
cnk(n,k) end.
-
Заметим, что собственно генерация сочетаний производится в рекурсивной подпрограмме gen. Она имеет следующие параметры: m — сколько элементов из множества нам еще осталось выбрать и L — начиная с какого элемента исходного множества следует выбирать этиm элементов. Обратите внимание, что именно вложенная структура описания процедур cnk и gen позволяет не передавать при рекурсивных вызовах значения n и k, а из основной программы обращаться к процедуреcnk с параметрами, соответствующими постановке задачи, не вдаваясь в подробности ее решения. Такой способ будем применять и в дальнейшем.
-
Генерация всех подмножеств данного множества
-
При решении олимпиадных задач чаще всего заранее неизвестно, сколько именно элементов исходного множества должно входить в искомое подмножество, то есть необходим перебор всех подмножеств. Однако если требуется найти минимальное подмножество, то есть состоящее как можно из меньшего числа элементов (или максимальное подмножество), то эффективнее всего организовать перебор так, чтобы сначала проверялись все подмножества, состоящие из одного элемента, затем из двух, трех и т.д. элементов (для максимального подмножества — в обратном порядке). В этом случае первое же подмножество, удовлетворяющее условию задачи, и будет искомым и дальнейший перебор следует прекратить. Для реализации такого перебора можно воспользоваться, например, процедурой cnk, описанной в предыдущем разделе. Введем в нее еще один параметр: логическую переменную flag, которая будет обозначать, удовлетворяет текущее сочетание элементов условию задачи или нет. При получении очередного сочетания вместо его печати обратимся к процедуре его проверки check, которая и будет определять значение флага. Тогда начало процедуры gen следует переписать так:
-
procedure gen(m, L: integer);
var i: integer;
begin
if flag then exit;
if m = 0 then
begin check(p,k,flag);
end
else ...
-
Далее процедура дословно совпадает с предыдущей версией. В основной же программе единственное обращение к данной процедуре следует заменить следующим фрагментом:
-
k := 0;
flag := false;
repeat k := k + 1;
cnk(n,1,flag) until flag or (k = n);
if flag then print(k)
else writeln('no solution');
-
Очевидно также, что в основной программе запрос значения переменной k теперь не производится.
-
Существует также альтернативный подход к перебору всех подмножеств того или иного множества. Каждое подмножество можно охарактеризовать, указав относительно каждого элемента исходного множества, принадлежит оно данному подмножеству или нет. Сделать это можно, поставив в соответствие каждому элементу множества 0 или 1. То есть каждому подмножеству соответствуетn-значное число в двоичной системе счисления (строго говоря, так как числа могут начинаться с произвольного количества нулей, которые значащими цифрами не считаются, то следует заметить, чтов соответствие ставятся n- или менее значные числа). Отсюда следует, что полный перебор всех подмножеств данного множества соответствует перебору всех чисел в двоичной системе счисления от
-
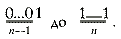
-
Теперь легко подсчитать и количество различных подмножеств данного множества. Оно равно 2 n — 1 (или 2 n , с учетом пустого множества). Таким образом, сопоставляя два способа перебора всех подмножеств данного множества, мы получили следующую формулу:
-
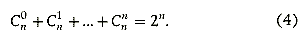
-
То есть в рамках сделанной выше оценки на количество допустимых вариантов в переборе мы можем рассмотреть все подмножества исходного множества только при n 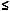 20.
20.
-
Прежде чем перейти к рассмотрению программ, соответствующих второму способу перебора, укажем, когда применение этих программ целесообразно. Во-первых, данные программы легко использовать, когда необходимо в любом случае перебрать все подмножества данного множества (например, требуется найти все решения, удовлетворяющие тому или иному условию). Во-вторых, когда с точки зрения условия задачи не имеет значения, сколько именно элементов должно входить в искомое подмножество. На примере такой задачи мы и напишем программу генерации всех подмножеств исходного множества в лексикографическом порядке. Задача взята из книги [5].
-
Условие. Даны целочисленный массив a [1..N] (N 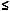 20) и число M. Найти подмножество элементов массива a[i1], a[i2], ..., a[ik] такое, что1
20) и число M. Найти подмножество элементов массива a[i1], a[i2], ..., a[ik] такое, что1 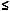 i1
i1 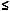 N и a[i1] + a[i2] ++ ... + a[ik] = M.
N и a[i1] + a[i2] ++ ... + a[ik] = M.
-
Решение. В качестве решения приведем процедуру генерации всех подмножеств, которые можно составить из элементов массива, и функцию проверки конкретного подмножества на соответствие условию задачи.
-
function check(j: longint): boolean;
var k: integer; s: longint;
begin
s := 0;
for k := 1 to n do
{данное условие означает, что в k-й справапозиции числа j, во 2-й системе, стоит 1}
if ((j shr (k — 1)) and 1) = 1
then s := s + a[k];
if s = m then
begin
for k := 1 to n do
if ((j shr (k — 1)) and 1) = 1
then write(a[k]:4);
writeln
end
end;
-
procedure subsets(n: integer);
var q,,j: longint;
begin
{помещаем в q число 2^n}
q := 1 shl n;
{цикл по всем подмножествам}
for j := 1 to q — 1 do
if check(j) then exit
end ;
-
Заметим, что если все элементы в массиве положительные, то, изменив порядок рассмотрения подмножеств, решение приведенной выше задачи можно сделать более эффективным. Так, если сумма элементов какого-либо подмножества уже больше, чем M, то рассматривать подмножества, включающие его в себя, ужене имеет смысла. Пересчет же сумм можно оптимизировать, если каждое следующее сгенерированное подмножество будет отличаться от предыдущего не более чем на один элемент (такой способ перечисления подмножеств показан в [2]). Приведенная же программа чрезвычайно проста, но обладает одним недостатком: мы не можем ни в каком случае с ее помощью перебирать все подмножества множеств, состоящих из более чем 30 элементов, что обусловлено максимальным числом битов, отводимых на представление целых чисел в Турбо Паскале (32 бита). Но, как уже было сказано выше, на самом деле перебор всех подмножеств у множеств большей размерности вряд ли возможен за время, отведенное для решения той или иной задачи.
-
Генерация всех перестановок n-элементногомножества
-
Количество различных перестановок множества, состоящего из n элементов, равно n!. В этом нетрудно убедиться: на первом месте в перестановке может стоять любой из n элементов множества, после того как мы на первом месте зафиксировали какой-либо элемент, на втором месте может стоять любой из n — 1 оставшегося элемента и т.д. Таким образом, общее количество вариантов равноn(n — 1)(n — 2) ... 3•2•1 = n!. То есть рассматривать абсолютно все перестановки мы можем только у множеств, состоящих из не более чем 10 элементов.Рассмотрим рекурсивный алгоритм, реализующий генерацию всех перестановок в лексикографическом порядке. Такой порядок зачастую наиболее удобен при решении олимпиадных задач, так как упрощает применение метода ветвей и границ, который будет описан ниже.Обозначим массив индексов элементов — p. Первоначально он заполнен числами 1, 2, ..., n, которые в дальнейшем будут меняться местами. Параметром i рекурсивной процедуры Perm служит место в массиве p, начиная с которого должны быть получены все перестановки правой части этого массива. Идея рекурсии в данном случае следующая: на i-м месте должны побывать все элементы массива p с i-го по n-й, и для каждого из этих элементов должны быть получены все перестановки остальных элементов, начиная с ( i + 1)-го места, в лексикографическом порядке. После получения последней из таких перестановок исходный порядок элементов должен быть восстановлен.
-
{описание переменных совпадает с приведенным выше}
procedure Permutations(n: integer);
procedure Perm(i: integer);
var j, k: integer;
begin
if i = n then
begin
for j := 1 to n do
write(a[p[j]],' ');
writeln
end
else
begin
for j := i + 1 to n do
begin
Perm(i + 1);
k := p[i];
p[i] := p[j];
p[j] := k
end ;
Perm(i + 1);
{циклический сдвиг элементов i..n влево}
k := p[i];
for j := i to n — 1 do
p[j] := p[j + 1];
p[n] := k
end
end;{Perm}
-
begin {Permutations}
Perm(1)
end;
-
begin {Main}
readln(n);
for i := 1 to n do
p[i] := i;{массив a может быть заполнен произвольно}
a := p;
Permutations(n) end.
-
Заметим, что в данной программе массив p можно было и не использовать, а переставлять непосредственно элементы массива a.
-
Разбиения множества
-
Число разбиений n-элементного множества на k блоков произвольного размера, но таких, что каждый элемент множества оказывается “приписан” к одному из блоков, выражается числом Стирлинга второго рода S(n, k) [6, 7]. Очевидно, что S(n, k) = 0 для k n. Если согласиться, что существует только один способ разбиения пустого множества на нулевое число непустых частей, тоS(0, 0) = 1 (именно такая договоренность, как и в случае с факториалом, приводит в дальнейшем к универсальным формулам). Так как при разбиении непустого множества нужна по крайней мере одна часть,S(n , 0) = 0 при n 0. Отдельно интересно также рассмотреть случай k = 2. Если непустое множество разделили на две непустые части, то в первой части может оказаться любое подмножество исходного множества, за исключением подмножеств, включающих в себя последний элемент множества, а оставшиеся элементы автоматически попадают во вторую часть. Такие подмножества можно выбрать 2n-1 способами, что и соответствует S(n, 2) при n 0.
-
Для произвольного k можно рассуждать так. Последний элемент либо будет представлять собой отдельный блок в разбиении, и тогда оставшиеся элементы можно разбить уже на k — 1 частей S(n — 1, k — 1) способами, либо помещаем его в непустой блок. В последнемслучае имеется kS(n — 1, k) возможных вариантов, поскольку последний элемент мы можем добавлять в каждый блок разбиения первых n — 1 элементов на k частей. Таким образом,
-
S(n, k) = S(n — 1, k — 1) + kS(n — 1, k),n 0. (5)
-
Полезными могут оказаться также формулы, связывающие числа Стирлинга с биномиальными коэффициентами, определяющими число сочетаний:
-
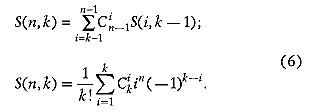
-
Если же значение k теперь не фиксировать и рассмотреть все разбиения n-элементного множества, то их количество выражается числом Белла
-

-
По формулам (7) можно подсчитать, что в рамках принятых выше допущений можно построить все разбиения множества, состоящего не более чем из 15 элементов (B15 = 1382958545).
-
Перейдем теперь к рассмотрению способа генерации всех разбиений исходного множества. Прежде всего следует договориться о том, как обозначать текущее разбиение. Так как в каждом из разбиений участвуют все элементы исходного множества, будем в массиве индексов p записывать, в какой блок попадает каждый из элементов в текущем разбиении. Параметр i в рекурсивной процедуре partозначает, что на текущем шаге мы именно i-й элемент будем размещать в каждом из допустимых для него блоков, а j как раз и определяет максимальный номер допустимого блока. После того как i-й элемент помещен в один из блоков, рекурсивно решается такая же задача уже для следующего элемента (в данном случае фактически работает универсальная схема перебора с возвратом [8]).
-
procedure partition(n: integer; var p: list);
procedure part(i, j: integer);
var l: integer;
begin
if i n then print(n, p)
else
for l := 1 to j do
begin
p[i] := l;
if l = j then part(i + 1, j + 1)
else part(i + 1, j)
end
end; {part}
-
begin {partition}
part(1,1)
end;
-
Как ни странно, в данном случае процедура print оказывается совсем не тривиальной, если требуется печатать (или анализировать) элементы каждого из блоков разбиения в отдельности. Поэтому приведем возможный вариант ее реализации (как и ранее, распределяли по блокам мы индексы, а печатаем или анализируем сами элементы исходного массива a):
-
procedure print(n: integer; var p: list);
var i, j, imax: integer;
begin
{определяем количество блоков в разбиении}
imax := 1; for i := 2 to n do
if p[i] imax then imax := p[i];
for i := 1 to imax do
{цикл по блокам}
begin
for j := 1 to n do
if p[j] = i then write(a[j]:4);
write(' |')
{блок напечатан}
end;
writeln {разбиение напечатано}
end;
-
Вложенного цикла можно избежать, если требуется, например, подсчитать сумму элементов в каждом из блоков. Тогда, используя дополнительный массив, мы, просматривая элементы массива a последовательно, будем увеличивать значения суммы для блока, соответствующего рассматриваемому элементу (аналогично операции,осуществляемой в алгоритме сортировки подсчетом).
-
Если при этом рассматривать массив p как n-значноечисло в n -ричной системе счисления, то можно ввестипонятие лексикографического порядка для разбиениймножества и ставить задачи определения номера разбиения и обратную ей. Как и ранее (см. [1—3]), они решаются методом динамического программирования и неиспользуют непосредственную генерацию всех разбиений.
-
Для полноты рассмотрения данной темы самостоятельно измените процедуру partition так, чтобы онагенерировала все разбиения, состоящие не более чем из k блоков. После этого напишите процедуру разбиения множества уже на ровно k непустых частей.
-
Олимпиадные задачи, использующие комбинаторные конфигурации
-
Пример 1. На одном острове Новой Демократии каждый из его жителей организовал партию, которую сам и возглавил. Отметим, что, ко всеобщему удивлению, даже в самой малочисленной партии оказалось не менее двух человек. К сожалению, финансовые трудности не позволили создать парламент, куда вошли бы, как предполагалось по Конституции острова, президенты всех партий. Посовещавшись, островитяне решили, что будет достаточно, если в парламенте будет хотя бы один член каждой партии. Помогите островитянам организовать такой, как можно более малочисленный, парламент, в котором будут представлены члены всех партий.
-
Исходные данные: каждая партия и соответственно ее президент имеют одинаковый порядковый номер от 1 до N (4 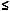 N
N 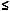 150). Вам даны списки всех N партийострова Новой Демократии. Выведите предлагаемый вами парламент в виде списка номеров его членов. (Олимпиада стран СНГ, г. Могилев, 1992 г.)
150). Вам даны списки всех N партийострова Новой Демократии. Выведите предлагаемый вами парламент в виде списка номеров его членов. (Олимпиада стран СНГ, г. Могилев, 1992 г.)
-
Решение. C теоретической точки зрения данная задача совпадает с задачей генерации всех подмножеств из множества жителей острова Новой Демократии. Причем наиболее подходящим кажется первый подход к решению данной задачи, связанный с генерацией различных сочетаний, начиная с одного жителя. Для полноты изложения этого подхода опишем функцию сheck, которуюследует применить в данной задаче. Исходные данные следует записать в массив s:array[1..150] of set of1..150 , заполнив каждый из n первых элементов этого массива множеством тех партий, в которых состоит тот или иной житель. Тогда функция проверки сочетания из элементов этого массива примет следующий вид:
-
function check(var p: list;k: integer): boolean;
var i: integer; ss: set of 1..150;
begin
ss := [];
for i := 1 to k do
ss := ss + s[p[i]];
check := (ss= [1..n]) end;
-
Как видно из описания функции, использование типа “множество” позволяет не только упростить данную программу, но и существенно ускорить ее выполнение по сравнению с работой с массивами. Однако большая размерность данной задачи не позволяет считать приведенное решение удовлетворительным во всех случаях. Так, уже для n = 100 перебор всех сочетаний из 4 и менее жителей приводит к рассмотрению около 4 миллионов вариантов. Для построения кода, пригодного для решения данной задачи при любых входных данных, несколько изменим описание массива s:
-
s: array[1..150] of
record name,number: integer;
partys: set of 1..150
end;
-
Здесь поле partys совпадает по смыслу с первоначальным описанием массива s, поле name cоответствует номеру (то есть фактически имени) жителя, и первоначально данное поле следует заполнить числами от 1 до n cогласно индексу элемента в массиве записей, и полеnumber соответствует количеству элементов во множестве из поля partys, то есть имеет смысл сразу подсчитать, в каком количестве партий состоит тот или иной житель. Теперь следует отсортировать массив s по убыванию значений поля number. Верхнюю оценку для числа членов парламента (kmax) подсчитаем, построив приближенное решение данной задачи следующим образом: во-первых, включим в парламент жителя, состоящего в максимальном количестве партий, затем исключим эти партии из остальных множеств и заново найдем в оставшемся массиве элемент с максимальным значением поля number (уже пересчитанного) и включимего в парламент, и так далее, до тех пор, пока сумма значений пересчитанных полей number у жителей, включенных в парламент, не будет равна n. Найденное количество членов парламента и будет kmax.
-
Теперь следует рассматривать сочетания из ( kmax — 1) элемента, затем из ( kmax — 2) и т.д. элементов. Если для сочетаний из какого-то рассматриваемого количества элементов k решение найдено не будет, то это означает, что точным является решение с количеством членов парламента k + 1 . Так как массив s упорядочен, то если решение для того или иного значения k существует, то скорее всего оно будет найдено при рассмотрении в лексикографическом порядке первых же сочетаний по k элементов. Поэтому временнаЯ трудоемкость в переборе возникает, только если решения c данным значением k не существует. В такой ситуации можно воспользоваться следующим “ненаучным” приемом: на поиск решения для каждого k, меньшего, чем kmax,отведем фиксированное количество времени, скажем, 2—3 секунды (точнее данное время стоит определить экспериментальным путем). Если за отведенное время решение не найдено, то следует считать полный перебор невозможным и закончить выполнение программы. В любом случае мы будем иметь какое-либо решение исходной задачи: точное или приближенное, то есть иногда содержащее больше членов парламента, чем минимально возможно. Однако на практике такой подход почти всегда приводит к точному решению, в силу перебора “с предпочтением”, проводимого для каждого k(невозможность проведения полного перебора для какого-либо k на практике соответствует отсутствию решения для данного k).
-
Пример 2. Дан автобусный билет с номером, состоящим из N цифр. Расставить между цифрами знаки арифметических операций “+”,“–”, “ * ”, “/” (целочисленное деление) и скобки таким образом, чтобы значение полученного выражения было равно 100. Можно образовывать многозначные числа из стоящих рядом цифр.Выражение должно быть корректным с точки зрения арифметики. Допустимы лишние скобки, не нарушающие корректности выражения. При вычислениях используется стандартный приоритет операций, число цифр N в номере билета не больше 6. ( V Всероссийская олимпиада по информатике, г. Троицк, 1993 г.)
-
Решение. Для построения универсального алгоритма решения данной задачи будем считать слияние двух соседних цифр одной из операций. Тогда между каждой парой соседних цифр может стоять одна из 5 операций. Для N цифр получаем 5 N—1 различных вариантов расстановки операций. Перебирать все варианты расстановки операций удобнее всего с помощью рассмотрения всех чисел в 5-ричной системе счисления, состоящих не болееч ем из N — 1 цифры, то есть для N = 6 от 00000 до 44444. Для перебора таких чисел необходимо написать процедуру прибавления 1 в 5-ричной системе счисления. Для каждого из вариантов расстановки операций перейдем от исходного массива из N цифр билета к массиву из К чисел, где K = (N — количество операций слияния цифр в рассматриваемом варианте). Теперь мы должны рассмотреть все перестановки из K — 1 арифметической операции в данном варианте. Каждая перестановка соответствует одному из порядков выполнения арифметических операций. Так, для 4 чисел перестановка номеров операций 3, 1, 2 означает, что сначала нужно выполнить арифметическое действие между 3-м и 4-м числом, затем между 1-м и 2-м и затем оставшееся. Если результат выполнения действий данного варианта в порядке, соответствующем текущей перестановке, равен искомому числу 100, то задача решена и можно перейти к печати результата. Для данной задачи возможны и более эффективные решения, но в силу ее небольшой размерности комбинаторный перебор оказывается вполне приемлемым.
-
Пример 3 . Губернатор одной из областей заключил с фирмой “HerNet” контракт на подключение всех городов области к компьютерной сети. Сеть создается следующим образом: в области устанавливаются несколько станций спутниковой связи, и затем от каждого города прокладывается кабель до одной из станций. Технология, используемая компанией, требует при увеличении расстояния увеличения толщины кабеля. Таким образом, стоимость кабеля, соединяющего город со станцией, при используемой компанией технологии будет равна kL2 , гдеL — расстояние от города до станции, а k — некий коэффициент. Вам требуется написать программу, определяющую минимальные затраты компании на установку сети.
-
Входные данные . Во входном файле записано числоn (1 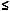 n
n 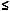 10) — количество городов в области. Затем идут положительные вещественные числа: k — коэффициент стоимости кабеля и P — стоимость постройки одной станции. Далее следуют n пар вещественных чисел, задающих координаты городов на плоскости.
10) — количество городов в области. Затем идут положительные вещественные числа: k — коэффициент стоимости кабеля и P — стоимость постройки одной станции. Далее следуют n пар вещественных чисел, задающих координаты городов на плоскости.
-
Выходные данные . В первую строку выходного файла нужно вывести минимальные затраты на установку сети (с тремя знаками после десятичной точки), во вторую — количество устанавливаемых станций. Далее вывести координаты станций (с тремя знаками последесятичной точки), а затем — список из n целых чисел, в котором i-е число задает номер станции, к которой будет подключен i-й город. ( Кировский командный турнир по программированию, 2000 г.)
-
Решение. В силу небольшой размерности мы можем рассмотреть все возможные варианты разбиения городов на группы, подразумевая, что для каждой группы будет установлена своя станция, причем оптимальным образом (найти оптимальное местонахождение станции для одной группы городов можно по формуле, аналогичной формуле нахождения центра масс). Затем нужно из всех разбиений выбрать то, для которого общая сумма затрат на установку сети будет минимальной.
-
-
Литература
-
1. Окулов С.М. Перестановки. “Информатика”, № 7/2000.
2. Окулов С.M. Комбинаторные задачи. “Информатика”,№ 10, 13/2000.
3. Усов Б.Б. Комбинаторные задачи. “Информатика”,№ 39/2000.
4. Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы. Построение и анализ. М.: МЦНМО, 2000.
5. Брудно A.Л., Каплан Л.И. Московские олимпиады попрограммированию. М.: Наука, 1990.
6. Кнут Д. Конкретная математика. Основание информатики. М.: “Мир”, 1998.
7. Липский В. Комбинаторика для программистов. М.:“Мир”, 1988.
8. Андреева Е.В. Еще раз о задачах на полный перебор вариантов. “Информатика”, № 45/2000 .
-
-
 Главная Главная -
 Материалы от Гергеля Материалы от Гергеля | 1. Идея метода динамического программирования Динамическое программирование является одним из методов решения задач, в которых задачу большой размерности можно решать, опираясь на уже решенные задачи меньшего размера. Словосочетание «динамическое программирование» впервые было использовано в 1940-х годах Р. Беллманом для описания процесса нахождения решения задачи, где ответ на одну задачу может быть получен только после решения задачи, «предшествующей» ей. Динамическое программирование может быть применено при выполнении следующих условий: 1) Существует способ выразить решение задачи через решение подзадач меньшей размерности. Этот способ задается рекуррентными соотношениями. 2) Существуют известные решения для задачи малой размерности (задача малой размерности решается просто). Динамическое программирование вычисляет решение для всех подзадач. Вычисление идет от малых подзадач к большим. Решения подзадач запоминаются в таблице. Мы заполняем эту таблицу независимо от того, нужна ли нам на самом деле конкретная подзадача для получения общего решения. Преимущество метода состоит в том, что раз уж задача решена, ее ответ хранится и никогда не вычисляется заново. Можно выделить два класса задач, решаемых методом динамического программирования. Задачи из первого класса связаны с вычислением сумм или произведений в зависимости от постановки задачи. Ко второму классу относятся оптимизационные задачи, для которых может быть сформулирован принцип оптимальности; суть принципа оптимальности состоит в том, что решения подзадач, используемые для нахождения оптимального решения задачи, также должны быть оптимальными. Мы рассмотрим на примерах использование метода динамического программирования для задач из обоих классов. 2. Рекуррентные соотношения Рекуррентные соотношения при использовании динамического программирования связывают решение задачи с решениями подзадач меньшей размерности. Приведем два примера задач, для которых можно записать такие рекуррентные соотношения. Задача о числах Фибоначчи. Задача состоит в вычислении N-ого числа в последовательности Фибоначчи 0, 1, 2, 3, 5, 8, ... , в которой первое число равно нулю, второе равно единице, а все остальные представляют собой сумму двух предыдущих чисел. Обозначим Fi число Фибоначчи, стоящее на i-м месте в последовательности (считаем 0 нулевым членом последовательности). Последовательность чисел Фибоначчи определяется рекуррентным соотношением F0 =0, F1 =1, Fi = Fi-1+ Fi-2 при i ≥ 1. (1) Задача о числе сочетаний. Для n-элементного множества сочетанием из n элементов по kназывается произвольное подмножество из k элементов. Например, для множества B={a,b,c,d} его подмножество {b,d} – это сочетание из 4-х элементов по 2. Обозначение применяется для числа всех сочетаний из n элементов поk. Так, для множества B множество всех двухэлементных подмножеств равно {{a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d}} и, следовательно, Величины называются также биномиальными коэффициентами. Известно рекуррентное соотношение для вычисления : , (2) позволяющее вычислять значение по значениям для числа сочетаний при меньших значениях параметров n и k. Заметим, что – быстро растущая функция, поэтому для вычислений по этой формуле нужна арифметика «больших чисел». 3. Динамическое программирование в задачах на поиск суммы 3.1. Числа Фибоначчи Формула (1) задает рекуррентное соотношение для чисел Фибоначчи, позволяющее решать задачу нахождения n-го числа Фибоначчи методом динамического программирования. Вычисление начинается с задания значений для первых двух чисел Фибоначчи: F0 =0, F1 =1. Таким образом, нам известны решения для самых маленьких подзадач. Далее по F0 и F1 мы вычисляем F2 , складывая F0 и F1, и запоминаем в таблице, по F1 и F2 находим F3 и его значение запоминаем в таблице, и т.д., до тех пор, пока не найдем n-е число Фибоначчи. Для хранения вычисляемых чисел Фибоначчи будем использовать одномерный массив F; элемент F[i] содержит значение Fi. Алгоритм на псевдокоде выглядит так: begin F[0] = 0 F[1] = 1 for i = 2 to n do F[i] = F[i-1]+F[i-2] вывести F[n] end Число ячеек используемой памяти для вычисления Fn имеет порядок n. Поскольку время вычислений пропорционально числу используемых ячеек массива F, трудоемкость алгоритма оценивается как O(n). Объем используемой памяти можно сократить, если заметить, что для вычисления очередного числа Фибоначчи используются только два предыдущих значения. Поэтому достаточно трех ячеек для запоминания чисел из последовательности Фибоначчи. 3.2. Треугольник Паскаля Из формулы (2) вытекает эффективный способ рекуррентного вычисления значений биномиальных коэффициентов, который можно представить в графической форме, известной как треугольник Паскаля. В этом равнобедренном треугольнике каждое число (кроме единиц на боковых сторонах) является суммой двух чисел, стоящих над ним. Число сочетаний находится в (n+1)-м ряду на (k+1)-м месте. | | | 1 | | | | | 1 | 1 | | | | 1 | 2 | 1 | | | 1 | 3 | 3 | 1 | | 1 | 4 | 6 | 4 | 1 | . . . . . . Рис. 1. Треугольник Паскаля Чтобы найти значение , достаточно последовательно заполнить таблицу по строкам для n = 1, 2, … , пока не дойдем до нужных значений n иk. Приведем описание на псевдокоде алгоритма вычисления числа сочетаний, в основе которого лежит метод динамического программирования. Алгоритм использует двумерный массив D, для элемента D[i, j] индекс i соответствует номеру строки таблицы в треугольнике Паскаля, индекс j – номеру столбца. procedure БИНОМ_КОЭФ(n,k) begin d[1,1]:=1 {заполнение первой строки таблицы} d[2,1]:=1; d[2,2]:=1 {заполнение второй строки таблицы} for i=3 to n+1 do begin d[i,1]:=1; d[i,i]:=1 {заполнение первого и последнего элементов в i-й строке треугольника Паскаля} for j=2 to i-1 do d[i,j]:= d[i-1,j-1]+d[i-1,j] {вычисление биномиального коэффициента по двум элементам предыдущей строки } end Вывести d[n+1,k+1] end Таблица для треугольника Паскаля занимает O(n2) ячеек памяти, но можно сократить ее до O(n), заметив, что для вычисления следующей строки нужна только предыдущая. Время работы алгоритма пропорционально числу заполненных клеток таблицы и имеет порядок n2. Применение метода динамического программирования позволяет во многих случаях улучшить трудоемкость алгоритма за счет сокращения дублирования вычислений. К примеру, для вычисления используются ранее вычисленные значения и , для вычисления которых в свою очередь используется значение . Если бы мы не хранили в таблице результаты всех предыдущих вычислений, пришлось бы вычислять дважды. Заметим, что уменьшение вычислительной сложности алгоритма достигается за счет увеличения объема используемой памяти. 4. Динамическое программирование в оптимизационных задачах. Перекрытие подзадач Метод динамического программирования может применяться для комбинаторных задач, в которых требуется найти оптимальное решение, то есть решение, дающее минимум (или максимум) некоторой целевой функции. Динамическое программирование применяется к решению таких задач, для которых может быть сформулирован принцип оптимальности, заключающийся в следующем: Частичные решения, т.е. решения подзадач, из которых получается решение всей задачи, являются оптимальными решениями этих подзадач. Применение принципа оптимальности к решению комбинаторных задач по существу означает использование принципа декомпозиции: вначале находятся оптимальные решения подзадач малого размера, затем они используются для отыскания оптимальных решений бóльших подзадач и, наконец, для решения самой задачи. Второе свойство задач, необходимое для использования динамического программирования – малость множества подзадач. Благодаря этому при рекурсивном решении задачи мы все время выходим на одни и те же подзадачи. В таком случае говорят, что у оптимизационной задачи имеются перекрывающиеся подзадачи. В типичных случаях количество подзадач полиномиально зависит от размера исходных данных. Алгоритмы, основанные на динамическом программировании, используют перекрытие подзадач следующим образом: каждая из подзадач решается только один раз, и ответ заносится в специальную таблицу; когда эта же подзадача встречается снова, программа не тратит время на ее решение, а берет готовый ответ из таблицы. Продемонстрируем использование метода динамического программирования на примере задачи триангуляции выпуклого многоугольника. 4.1. Оптимальная триангуляция многоугольника Прежде чем сформулировать задачу, введем некоторые определения. Многоугольник – это замкнутая кривая на плоскости, составленная из отрезков, называемых сторонами многоугольника. Многоугольник называется выпуклым, если для любых двух точек, лежащих внутри или на границе многоугольника, соединяющий их отрезок целиком лежит внутри или на границе многоугольника. Диагональ многоугольника – это отрезок, соединяющий две вершины, не являющиеся соседними. Выпуклый многоугольник можно задать, перечислив его вершины в порядке обхода по часовой стрелке. Будем считать, что многоугольник имеет n вершин v1, v2, … , vn, заданных своими координатами на плоскости. Под триангуляцией будем понимать набор непересекающихся диагоналей, которые разбивают многоугольник на треугольники. Триангуляцию можно также определить как наибольшее множество непересекающихся диагоналей. Многоугольник может иметь несколько различных триангуляций, но все они состоят из n-3 диагоналей и разбивают многоугольник на n-2 треугольника. Примеры триангуляций семиугольника приведены на рис. 2. Стоимость триангуляции определим как сумму длин диагоналей. Задача о триангуляции многоугольника состоит в нахождении триангуляции с наименьшей стоимостью. SHAPE \* MERGEFORMAT
| Рис. 2. Две триангуляции одного семиугольника | Пусть в оптимальной триангуляции присутствует диагональ (vi, vj). Область n-угольника, отсекаемую диагональю (vi, vj), будем описывать последовательностью номеров вершин (vi, vi+1, … , vj) в порядке обхода границы области по часовой стрелке. Диагональ разбивает исходный многоугольник на два выпуклых многоугольника с меньшим числом вершин. Очевидно, для каждого из двух образованных многоугольников их диагонали, входящие в оптимальную триангуляцию n-угольника, также определяют на этих многоугольниках оптимальную триангуляцию. В этом проявляется принцип оптимальности для задачи о триангуляции: оптимальной триангуляции всего n-угольника соответствуют оптимальные триангуляции в его областях, отсекаемых диагоналями. Основываясь на принципе оптимальности, обсудим порядок решения задачи. Рассмотрим треугольники, каждый из которых образован некоторой диагональю и двумя соседними сторонами многоугольника. Определим их стоимость равной нулю. Очевидно, число таких «коротких» диагоналей равно n. На первом этапе решим задачу триангуляции для четырехугольников, каждый из которых образован четырьмя последовательными вершинами n-угольника и некоторой диагональю. Таких диагоналей n штук и, следовательно, столько же и четырехугольников. На втором этапе решим задачу триангуляции для пятиугольников, каждый из которых образован пятью последовательными вершинами n-угольника и некоторой диагональю. Таких диагоналей n штук и, следовательно, столько же и пятиугольников. И т.д. На предпоследнем, (n-4)-м этапе будут решены задачи триангуляции для (n-1)-угольников, и на последнем, (n-3)-м этапе мы получим решение исходной задачи. Перейдем к описанию рекуррентного соотношения. Обозначим через C(i, j) длину диагонали n-угольника, соединяющей вершины vi и vj. C(i, j) находим по координатам вершин vi и vj, используя формулу для расстояния между двумя точками на плоскости: . Определим T(i, j) как стоимость оптимальной триангуляции j-угольника с начальной вершиной обхода границы vi. Положим T(i, 2)=0 и T(i, 3)=0 для i=1,2, … ,n. При cправедливо следующее рекуррентное соотношение: (3) (В случае если при вычислениях мы получим номер вершины, больший n, возьмем его по модулю n). Поясним равенство (3). Оптимальная триангуляция j-угольника при может быть получена одним из трех способов (см. рис. 3). 1) Триангуляция может быть получена из оптимальной триангуляции (j-1)-угольника с границей (vi, vi+1, … , vi+j-2), если в триангуляции j-угольника есть диагональ (vi ,vi+j-2). Тогда , т.е. складывается из стоимости триангуляции (j-1)-угольника и длины диагонали (vi, vi+j-2). 2) Триангуляция может быть получена из оптимальной триангуляции (j-1)-угольника с границей (vi+1, vi+2, … , vi+j-1), если в триангуляции j-угольника есть диагональ (vi+1 ,vi+j-1). Тогда . 3) Третий способ получается, если треугольник со стороной (vi+1,vi+j-1) образуется в триангуляции j-угольника с помощью еще двух диагоналей (vi ,vk) и (vk, vi+j-1), где k – некоторая промежуточная вершина при обходе границы j-угольника. В этом случае оптимальная триангуляция j-угольника складывается из оптимальных триангуляций двух многоугольников меньшего размера: многоугольника с границей (vi, vi+1, … , vk) и многоугольника с границей (vk, vk+1, … , vi+j-1) с добавлением двух диагоналей (vi ,vk) и (vk, vi+j-1). Поэтому к стоимости двух оптимальных триангуляций меньших многоугольников добавляются длины диагоналей (vi ,vk) и (vk, vi+j-1). . Можно немного упростить написание формулы (3), если положитьC(i,k)=0 в случае, когда vi и vk являются соседними вершинами n-угольника. Тогда рекуррентное соотношение (3) эквивалентно соотношению . (4) Таким образом, используя рекуррентное соотношение (4), сначала находим стоимости оптимальных триангуляций для всех четырехугольников и заносим результаты в таблицу, затем, используя
| Рис. 3. Способы получения триангуляции j-угольника |
запомненные результаты и рекуррентное соотношение для j=5, решаем задачу триангуляции для всех пятиугольников, и т.д. Продолжаем процесс до тех пор, пока не найдем стоимость оптимальной триангуляции n-угольника. Результаты вычислений последовательно запоминаем в таблице и используем при необходимости, а не вычисляем заново. 4.2. Пример решения задачи о триангуляции Проиллюстрируем решение задачи о триангуляции на примере семиугольника, заданного следующими координатами своих вершин: | | v1 | v2 | v3 | v4 | v5 | v6 | v7 | | x | 0 | 0 | 8 | 15 | 27 | 22 | 10 | | y | 10 | 20 | 26 | 26 | 21 | 12 | 0 | Этап 1. При j =4 формулу (4) можно переписать в виде . Применяя эту формулу, заполним первую строку таблицы значениями для i =1,2, … , 7. Этап 2. При j = 5 формула (4) принимает вид . Применяя эту формулу, заполним вторую строку таблицы значениями для i =1,2, … , 7. Этап 3. При j = 6 формула (4) принимает вид . Используя ее, заполняем четвертую строку таблицы значениями для i =1,2, … , 7. Этап 4. При j=7 существует единственный (исходный) 7-угольник, поэтому достаточно вычислить T(1,7): . В результате вычислений получим табл. 1. Таблица 1. Стоимости минимальных триангуляций для подзадач семиугольника | i j | 1 | 2 | 3 | 4 | 5 | 6 | 7 | | 4 | 16,16 | 16,16 | 15,65 | 15,65 | 22,05 | 22,09 | 17,89 | | 5 | 37,54 | 31,81 | 35,45 | 37,74 | 45,50 | 39,98 | 38,09 | | 6 | 53,34 | 55,22 | 57,54 | 59,67 | 59,78 | 59,78 | 63,61 | | 7 | 75,43 | | | | | | | Из таблицы находим, что стоимость минимальной триангуляции равна 75,43. Таблица, построенная в результате вычислений, позволяет определить стоимость оптимальной триангуляции, из нее непосредственно нельзя определить саму минимальную триангуляцию, так как для этого надо знать значение k, которое обеспечивает минимум в формуле (4). Если мы знаем значение k, тогда решение состоит из диагоналей (vi ,vk) и (vk ,vi+j-1) (исключая случай k=i+1 или k=i+j-2) плюс диагонали, указываемые решениями T(i, k+1) и T(i+k, j- k +1). Поэтому при вычислении элементов таблицы полезно включить в нее значения k, при которых получается минимум в формуле (4). Оптимальная триангуляция рассматриваемого семиугольника приведена на рис. 4. SHAPE \* MERGEFORMAT
| Рис. 4. Триангуляция с минимальной стоимостью | 4.3. Трудоемкость задачи триангуляции многоугольника при использовании динамического программирования Несколько слов о вычислительной сложности алгоритма, использующего метод динамического программирования. Таблица содержит O(n2) клеток, поэтому общее число решаемых подзадач полиномиально зависит от числа сторон заданного многоугольника. Для вычисления значения в клетке нам приходится вычислять минимум не более чем из n величин, каждая из которых является суммой не более чем четырех слагаемых. Поэтому для заполнения одной клетки требуется выполнить O(n) операций. Общая трудоемкость алгоритма имеет порядок n3. Полиномиальный алгоритм получился за счет запоминания оптимальных решений для всех подзадач; что позволило исключить дублирование вычислений. 5. Литература 5.1. Использованные источники информации -
Ахо А., Хопкрофт Дж., Ульман Дж. Построение и анализ вычислительных алгоритмов. – М.: Мир, 1979. – 536 с. -
Ахо А.А., Хопкрофт Д.Э., Ульман Д.Д. Структуры данных и алгоритмы. М.: Вильямс, 2007. – 400 с. -
Кормен Т.Х., Лейзерсон Ч.И., Ривест Р.Л., Штайн К. Алгоритмы: Построение и анализ,. 2-е издание, - М.: Издательский дом "Вильямс", 2005. - 1296 с. -
Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. – М.: Мир, 1980. – 480 с. 5.2. Дополнительная литература 1. Шень А. Программирование: теоремы и задачи. – 3-е изд. – М.: МЦНМО, 2007. – 296 с. |
|
Бесплатный конструктор сайтов - uCoz
Содержание
Введение
-
Предмет комбинаторики
-
Краткая историческая справка
-
Основные комбинаторные задачи
-
Основные формулы комбинаторики
-
Правило произведений
-
Правило суммы
Заключение
Список использованной литературы
Введение
Задачи дискретной математики, к которым относится большинство олимпиадных задач по информатике, часто сводятся к перебору различных комбинаторных конфигураций объектов и выбору среди них наилучшего, с точки зрения условия той или иной задачи. Поэтому знание алгоритмов генерации наиболее распространенных комбинаторных конфигураций является необходимым условием успешного решения олимпиадных задач в целом. Важно также знать количество различных вариантов для каждого типа комбинаторных конфигураций, так как это позволяет реально оценить вычислительную трудоемкость выбранного алгоритма решения той или иной задачи.
1. Предмет комбинаторики
Наблюдаемые нами события (явления) можно подразделить на следующие три вида: достоверные, невозможные и случайные.
Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S. Например, если в сосуде содержится вода при нормальном атмосферном давлении и температуре 20°, то событие «вода в сосуде находится в жидком состоянии» есть достоверное. В этом примере заданные атмосферное давление и температура воды составляют совокупность условий S.
Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S. Например, событие «вода в сосуде находится в твердом состоянии» заведомо не произойдет, если будет осуществлена совокупность условий предыдущего примера.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти. Например, если брошена монета, то она может упасть так, что сверху будет либо герб, либо надпись. Поэтому событие «при бросании монеты выпал «герб» — случайное. Каждое случайное событие, в частности выпадение «герба», есть следствие действия очень многих случайных причин (в нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, — она просто не в силах это сделать.
По-иному обстоит дело, если рассматриваются случайные события, которые могут многократно наблюдаться при осуществлении одних и тех же условий S, т. е. если речь идет о массовых однородных случайных событиях. Оказывается, что достаточно большое число однородных случайных событий независимо от их конкретной природы подчиняется определенным закономерностям, а именно вероятностным закономерностям. Установлением этих закономерностей и занимается теория вероятностей.
Итак, предметом теории вероятностей является изучение вероятностных закономерностей массовых однородных случайных событий.
Знание закономерностей, которым подчиняются массовые случайные события, позволяет предвидеть, как эти события будут протекать. Например, хотя, как было уже сказано, нельзя наперед определить результат одного бросания монеты, но можно предсказать, причем с небольшой погрешностью, число появлений «герба», если монета будет брошена достаточно большое число раз. При этом предполагается, конечно, что монету бросают в одних и тех же условиях. Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.
В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и техники, способствуя их прогрессу.
2. Краткая историческая справка
Первые работы, в которых зарождались основные понятия теории вероятностей, представляли собой попытки создания теории азартных игр (Кардано, Гюйгенс, Паскаль, Ферма и другие в XVI—XVII вв.).
Следующий этап развития теории вероятностей связан с именем Якоба Бернулли (1654—1705). Доказанная им теорема, получившая впоследствии название «Закона больших чисел», была первым теоретическим обоснованием накопленных ранее фактов.
Дальнейшими успехами теория вероятностей обязана Муавру, Лапласу, Гауссу, Пуассону и др.
Новый, наиболее плодотворный период связан с именами П. Л. Чебышева (1821—1894) и его учеников А.А.Маркова(1856—1922) и А. М.Ляпунова (1857—1918). В этот период теория вероятностей становится стройной математической наукой. Ее последующее развитие обязано в первую очередь русским и советским математикам (С. Н. Бернштейн, В. И. Романовский, А. Н. Колмогоров, А. Я. Хинчин, Б. В. Гнеденко, Н. В. Смирнов и др.). В настоящее время ведущая роль в создании новых ветвей теории вероятностей также принадлежит советским математикам.
3. Основные комбинаторные задачи
Основными и типичными операциями и связанными с ними задачами комбинаторики являются следующие:
1) образование упорядоченных множеств, состоящее в установлении определенного порядка следования элементов множества друг за другом, - составление перестановок;
2) образование подмножеств, состоящее в выделении из данного множества некоторой части его элементов, - составление сочетаний;
3) образование упорядоченных подмножеств - составление размещений.
ТИПЫ КОМБИНАТОРНЫХ ЗАДАЧ.
1. Магический квадрат - квадратная таблица (n * n) целых чисел от 1 до n¤ такая, что суммы чисел вдоль любого столбца, любой строки и двух диагоналей таблицы равны одному и тому же числу s=n(n¤+1)/2. Число n называют порядом магического квадрата.
Доказано, что магический квадрат можно построить для любого n Є 3. Уже в средние века был известен алгоритм построения магических квадратов нечетного порядка. Существуют магические квадраты, удоволетворяющие ряду дополнительных условий, например магический квадрат с n=8 , который можно разделить на четыре меньших магических квадрата 4x4. В Индии и некоторых других странах магические квадраты употреблялись как талисманы. Однако общей теории магических квадратов не существует. Неизвестно даже общее число магических квадратов порядка n.
2. Латинский квадрат - квадратная матрица порядка n, каждая строка и каждый столбец которой являются перестановками элементов конечного множества S, состоящего из n элементов.
3. Задача размещения - одна из классических комбинаторных задач, в которой требуется определить число способов размещения m различных предметов в n различных ячейках с заданным числом r пустых ячеек. Это число равно
r n-r mC (r)=C дельта O , r=0,1,2,...,n,nm n
где
k m k j j m дельта O =сигма (-1) C (k-j) j=0 k
Задача коммивояжера, задача о бродячем торговце – комбинаторная задача теории графов. В простейшем случае формулируется следующим образом: даны n городов и известно расстояние между каждыми двумя городами; коммивояжер, выходящий из какого-нибудь города, должен посетить n-1 других городов и вернуться в исходный. В каком порядке должен он посещать города (по одному разу каждый) чтобы общее пройденное расстояние было минимальным?
Методы решения задачи коммивояжера, по существу, сводятся к организации полного перебора вариантов.
МЕТОДЫ РЕШЕНИЯ КОМБИНАТОРНЫХ ЗАДАЧ
1. Метод рекуррентных соотношений.
Метод рекуррентных соотношений состоит в том, что решение комбинаторной задачи с n предметами выражается через решение аналогичной задачи с меньшим числом предметов с помощью некоторого соотношения, которое называется рекуррентным. Пользуясь этим соотношением, искомую величину можно вычислить, исходя из того, что для небольшого количества предметов решение задачи легко находится.
2. Метод включения и исключения.
Пусть N(A) - число элементов множества A. Тогда методом математической индукции можно доказать, что
N(A1 U A2 U ... An) = N(A1) + ... + N(An) - - {N(A1 П A2) + ... + N(An-1 П An)} + + {N(A1 П A2 П A3) + ... + N(An-2 П An-1 П An)} - ...... +(-1)^n-1*N(A1 П A2 П ... П An-1 П An).
Метод подсчета числа элементов объединения множеств по этой формуле, состоящий в поочередном сложении и вычитании, называется методом включения и исключения.
3. Метод траекторий.
Для многих комбинаторных задач можно указать такую геометрическую интерпретацию, которая сводит задачу к подсчету числа путей (траекторий), обладающих определенным свойством.
4. Основные формулы комбинаторики
Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.
Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок
Pn = n!,
где n! = 1 * 2 * 3 ... n.
Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.
Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений
Amn = n (n - 1)(n - 2) ... (n - m + 1).
Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний
С mn = n! / (m! (n - m)!).
примеры перестановок, размещений, сочетаний
Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством
Amn = PmC mn.
Замечание. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n1 элементов одного вида, n2 элементов другого вида и т.д., то число перестановок с повторениями
Pn (n1, n2, ...) = n! / (n1! n2! ... ),
где n1 + n2 + ... = n.
5. Правило произведения
Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.
Произведение событий. Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А — деталь годная, В — деталь окрашенная, то АВ — деталь годна и окрашена.
Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С — появление «герба» соответственно в первом, втором и третьем бросаниях монеты, то АВС — выпадение «герба» во всех трех испытаниях.
Условная вероятность. Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий S.
Условной вероятностью РA (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.
Исходя из классического определения вероятности, формулу РA (В) = Р (АВ) / Р (А) (Р (А) 0 можно доказать. Это обстоятельство и служит основанием для следующего общего (применимого не только для классической вероятности) определения.
Условная вероятность события В при условии, что событие А уже наступило, по определению, равна
РA (В) = Р (АВ) / Р (А) (Р(A)0).
Рассмотрим два события: А и В; пусть вероятности Р (А) и РA (В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.
6. Правило суммы
Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.
Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А — попадание при первом выстреле, В — попадание при втором выстреле, то А + В — попадание при первом выстреле, или при втором, или в обоих выстрелах.
В частности, если два события А и B — несовместные, то А + В — событие, состоящее в появлении одного из этих событий, безразлично какого.
Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.
Пусть события A и В — несовместные, причем вероятности этих событий известны. Как найти вероятность того, что наступит либо событие A, либо событие В? Ответ на этот вопрос дает теорема сложения.
Теорема. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (А + В) = Р (А) + Р (В).
Доказательство:
Введем обозначения: n — общее число возможных элементарных исходов испытания; m1 — число исходов, благоприятствующих событию A; m2— число исходов, благоприятствующих событию В.
Число элементарных исходов, благоприятствующих наступлению либо события А, либо события В, равно m1 + m2. Следовательно,
Р (A + В) = (m1 + m2) / n = m1 / n + m2 / n.
Приняв во внимание, что m1 / n = Р (А) и m2 / n = Р (В), окончательно получим
Р (А + В) = Р (А) + Р (В).
Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:
Р (A1 + A2 + ... + An) = Р (A1) + Р (A2) + ... + Р (An).
Доказательство:
Рассмотрим три события: А, В и С. Так как рассматриваемые события попарно несовместны, то появление одного из трех событий, А, В и С, равносильно наступлению одного из двух событий, A + В и С, поэтому в силу указанной теоремы
Р ( А + В + С) = Р [(А + В) + С] = Р (А + В) + Р (С) = Р (А) + Р (В) + Р (С)
Заключение
Перечисленные подзадачи в программировании обычно рассматривают для следующих комбинаторных конфигураций: перестановки элементов множества, подмножества множества, сочетания из n элементов множества по k элементов (k-элементные подмножества множества, состоящего из nk элементов), размещения (упорядоченные подмножества множества, то есть отличающиеся не только составом элементов, но и порядком элементов в них), разбиения множества (множество разбивается на подмножества произвольного размера так, что каждый элемент исходного множества содержится ровно в одном подмножестве), разбиения натуральных чисел на слагаемые, правильные скобочные последовательности (различные правильные взаимные расположения n пар открывающихся и закрывающихся скобок).
Большинство указанных конфигураций были подробно рассмотрены в [1-3]. Однако при генерации различных конфигураций использовались в основном нерекурсивные алгоритмы. Опытные же участники олимпиад в подобных случаях при программировании используют в основном именно рекурсию, с помощью которой решение рассматриваемых задач зачастую можно записать более кратко и прозрачно. Поэтому для полноты изложения данной темы приведем ряд рекурсивных комбинаторных алгоритмов и рассмотрим особенности применения рекурсии в комбинаторике.
комбинаторика вероятность исторический программирование
Список использованной литературы
-
Окулов С.М. Перестановки. “Информатика”, №7, 2000.
-
Окулов С.M. Комбинаторные задачи. “Информатика”, №10, 13, 2000.
-
Усов Б.Б. Комбинаторные задачи. “Информатика”, №39, 2000.
-
Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы. Построение и анализ. М.: МЦНМО, 2000.
-
Брудно A.Л., Каплан Л.И. Московские олимпиады по программированию. М.: Наука, 1990.
-
Кнут Д. Конкретная математика. Основание информатики. М.: “Мир”, 1998.
-
Липский В. Комбинаторика для программистов. М.: “Мир”, 1988.
-
Андреева Е.В. Еще раз о задачах на полный перебор вариантов. “Информатика”, №45, 2000.
Размещено на Allbest.ru