Методическая разработка
открытого занятия с элементами информационно-коммуникативных технологий на тему:
«Нахождение наибольшего и наименьшего значения функции (при решении задач прикладного характера)»
Методическая цель занятия: реализация элементов информационно-коммуникативных технологий на практических занятиях; применение активных форм и методов воспитания личности компетентного специалиста.
Межпредметные связи:
обеспечивающие – алгебра и начала анализа за 10 кл. «Функция», геометрия 7-9 кл .;
обеспечиваемые – физика, высшая математика.
Тема. Нахождение наибольшего и наименьшего значения функции (при решении задач прикладного характера)
Цель:
учебная – проверить знания студентов формул для нахождения производной и умение применять методы дифференциального исчисления к решению прикладных задач, умение составлять алгоритм решения прикладных задач;
развивающая – формировать умение рассуждать, анализировать и делать выводы; развивать творческие способности и логическое мышление, кругозор студентов, устное и письменная речь;
воспитательная – воспитывать активность, внимание, интерес и желание иметь глубокие и прочные знания, развивать интерес к математике.
Тип урока: совершенствование знаний, умений и навыков.
Компетенции: учебная, информационная, стимулирующе-мотивационная.
Оборудование: ноутбук, проектор мультимедийный, линейка для работы на доске, маркеры разных цветов, наглядные пособия (презентация), раздаточный материал (опорные конспекты).
«Мало иметь хороший ум, главное – это хорошо применять его»
Р. Декарт
Ход урока
І. Организационный момент.
Приветствие, проверка готовности к уроку. Настройка на рабочую обстановку.
ІІ. Мотивация учебной деятельности. Объявление темы и задач урока.
На предыдущих уроках вы усвоили одно из фундаментальных понятий алгебры и начал анализа - производную. Ее появлению мы обязаны таким ученым, как П.Ферма, И. Ньютон, Лейбниц, Ж.Лагранжа.
Понятие производной широко применяется в механике, военном деле, медицине, космонавтике, физике, астрономии. Поэтому и уделяется такое внимание этому понятию.
Р. Декарт говорил: «Мало иметь хороший ум, главное - это хорошо применять его». Темой урока является «Нахождение наибольшего и наименьшего значения функции (при решении задач прикладного характера)». Основная цель нашего урока - использование теоретических знаний при решении практических задач.
ІІІ. Актуализация опорных знаний
1. Фронтальный опрос по технологии «Игра в пазл»
| 1. Дать определение производной? | Число, равное границы отношения приращения функции к соответствующему приращению аргумента при условии, что приращение аргумента стремится к нулю |
| 2. Признак возрастания функции | Если для всех x из некоторого промежутка f `(x) 0, то функция возрастает на этом промежутке |
| 3. Признак убывания функции | Если для всех x из некоторого промежутка f `(x) |
| 4. Назовите признак точки максимума функции | Если при переходе через точку x0 производная меняет знак с плюса на минус, то x0 – точка максимума |
| 5. Признак точки минимума функции | Если при переходе через точку x0 производная меняет знак с минуса на плюс, то x0 – точка минимума |
| 6. Какие точки могут быть экстремальными? | Точки в которых f `(x) = 0 или не существует в этой точке называют критическими точками первого рода или стационарными или подозрительными на экстремум. |
Как вы думаете, какое отношение имеют данные ученые раздел математики, который мы изучаем.
Лагранж внес существенный вклад во многие области математики, включая вариационное исчисление, теорию дифференциальных уравнений, решение задач на нахождение максимумов и минимумов, теорию чисел (теорема Лагранжа), алгебру и теорию вероятностей. Современное обозначение производной в виде штриха принадлежит Лагранжа.
Ньютон пришел к понятию производной, решая задачи о мгновенную скорость. Ньютону принадлежит также идея использования производных для нахождения корня нелинейного уравнения, чем внес вклад в численный анализ. Предложенный им метод называют методом касательных или методом Ньютона.
2. Знание таблицы производных и правил дифференцирования - это надежный шаг к решению многих задач.
Прием «Лови ошибку» (1 ученик у доски):
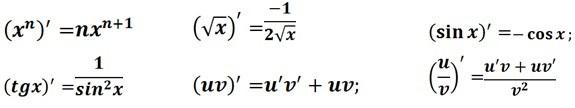
Прием «Найди соответствие» (работа в группах):

ІV. Применение умений и навыков
Давайте вспомним алгоритм нахождения наибольшего и наименьшего значения функции на отрезке.
Найти точки экстремума функции, т. Б. точки в которых производная равна нулю и меняет свой знак.
Вычислить значение функции в этих точках и на концах отрезка, где определена функция.
Выбрать из полученных значений функции наибольшее и наименьшее.
Как вы думаете, какие этапы нужно добавить к данному алгоритму, чтобы решить задачу прикладного содержания?
Первый этап: составить математическую модель задачи, т. Б. выразить искомую величину через функцию от некоторой переменной и найти область ее определения.
Последний этап: проанализировать результат и сделать обратную интерпретацию.
1. Коллективное выполнение задач под руководством учителя
1. Легенда об основании Карфагена говорит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно оградить одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремни, связала их и оградила получения ремнем большой участок земли, лежащей вдоль берега.
2. Пункт В находится на расстоянии 60 км от прямолинейной железной дороги. Расстояние по железной дороге от пункта А до ближайшего пункта В пункта С 285 км. На каком расстоянии от п. С нужно построить станцию Д, чтобы время движения путем АДВ был маленьким, если скорость движения по железной дороге 52 км / ч, а по грунтовой дороге 20 км / ч.
Решение:

По условию  ,
,  , следовательно
, следовательно  ,
,  ч.
ч.
 .
.
Рассмотрим функцию
 ,
,
Найдем  , при котором функция
, при котором функция  приобретает наименшего значения
приобретает наименшего значения
 .
.

 , следовательно станцию Д нужно строить в 25 км от станции С.
, следовательно станцию Д нужно строить в 25 км от станции С.
Самостоятельная работа (15 мин.)
Выполнить задачи:
1. Найти промежутки возрастания и убывания функции.
2. Найти экстремумы функции.
3. Найти наибольшее и можно меньше значение функции на отрезке [-1; 2]


(N – номер студента в журнале, студент по собственному желанию выбирает одну из функций и выполняет для нее три задачи, таблица оценки приведена ниже).
| 
| 
|
| номер задания | Оценка по 12-ти бальной шкале | номер задания | Оценка по 12-ти бальной шкале |
| 1 | 6 балів | 1 | 9 балів |
| 2 | 7 балів | 2 | 10 балів |
| 3 | 8 балів | 3 | 11 балів |
4. Психологическая минутка
Первая женщина-математик С.Ковалевской сказала: «Математик должен быть поэтом в душе».
Подберите к графиков функций, изображенных на рисунках, пословицы, раскрывающих сущность процессов функции.

Любишь с горки катиться, люби и саночки возить.
Повторение – мать учения.
Как крикнеться, так и откликнется.
V. Итог урока
Прием «Закончи предложение»
• Сегодня на уроке мы ...
• Важнейшим на уроке для меня было ...
• Больше всего заинтересовало ...
• Самым сложным для меня было ...
• Чтобы устранить пробелы в знаниях, я ...
VІ. Домашнее задание
1. Повторить таблицу производных элементарных функций.
Решить задачу:
Рекламный щит имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром. Определите его стоимость, если суммарная стоимость материалов и работы по изготовлению за 1 м² составляет 500 руб + 100 руб за погоней метр длины щита.





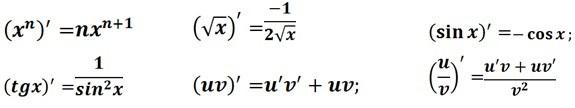


 ,
,  , следовательно
, следовательно  ,
,  ч.
ч. .
. ,
,
 , при котором функция
, при котором функция  приобретает наименшего значения
приобретает наименшего значения .
.
 , следовательно станцию Д нужно строить в 25 км от станции С.
, следовательно станцию Д нужно строить в 25 км от станции С.












