Учебная задача: Изучить следующие дидактические единицы: Определения: правильного многоугольника, центра правильного многоугольника; Теоремы: о величине угла правильного многоугольника, об окружности, описанной около правильного многоугольника, об окружности, вписанной в правильный многоугольник, следствий из этих теорем.
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика.
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения.
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
I. Мотивационно-ориентировочная часть (8 минут)
II. Операционно-познавательная часть (35 минут)
III. Рефлексивно-оценочная часть (2 минуты)
| Деятельность учителя | Деятельность учеников |
| Мотивационно-ориентировочная часть |
| Актуализация: Предваряющее домашнее задание: повторить определение многоугольника, виды многоугольников. |
| - Дома Вы повторили понятие и виды многоугольников. Сформулируйте пожалуйста определение.
- На какие группы можно разделить все многоугольники? - А какие многоугольники называются выпуклыми?
- За все время Вы изучали разные многоугольники, их свойства и признаки, но больше всего Вам приходилось работать именно с выпуклыми многоугольниками. | - Многоугольником называется часть плоскости, ограниченная замкнутой ломаной, звенья которой не пересекаются. - Выпуклые и невыпуклые многоугольники. - Выпуклым называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. |
| Мотивация |
| - Выпуклые многоугольники были известны еще в глубокой древности. В египетских и вавилонских старинных памятниках встречаются особенные четырехугольники, шестиугольники и восьмиугольники в виде изображений на стенах и украшений, высеченных из камня. Такие особенные многоугольники носят специальное название – правильные многоугольники. 
- Посмотрите вокруг: пчелы – удивительные творения природы. Свои геометрические способности они проявляют при построении своих сот, ведь ячейка на сотах имеет форму правильного шестиугольника. Строя шестиугольные ячейки пчелы наиболее экономно используют площадь внутри небольшого улья и воск для изготовления ячеек. 
- Многие простейшие морские организмы имеют форму правильных многоугольников 
- Снежинки имеют форму правильных многоугольников. 
|
| Постановка учебной задачи |
| - Итак, сегодня на уроке необходимо познакомиться с очень интересными, особыми фигурами – правильными многоугольниками, изучить понятие правильного многоугольника, некоторые свойства. |
| Операционно-познавательная часть |
| - Среди всех выпуклых многоугольников выделяют особые, у которых равны все стороны и равны все углы и называют их правильные многоугольники. Сформулируем определение: Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны, и все углы равны. -Частными случаями правильных многоугольников являются правильный треугольник, правильный четырехугольник, правильный пятиугольник и т.д. - Правильный треугольник Вы уже встречали в курсе геометрии. Посмотрите на изображение, какой треугольник является правильным? 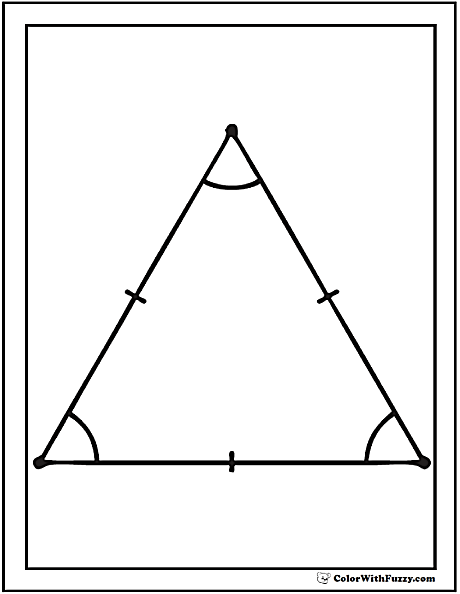
- Вспомните свойства, которыми обладает равносторонний, а значит правильный треугольник?
- В 8 классе Вы изучали выпуклые многоугольники, доказывалась теорема о том, что сумма углов выпуклого многоугольника находится по формуле: 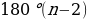 . .
- Итак, правильный многоугольник является выпуклым, тогда известна ли формула нахождения суммы углов правильного n-угольника? - Сколько углов в правильном n-угольнике? - Тогда как найти величину одного из n равных углов правильного многоугольника? - Правильно! Итак, запишем формулу для нахождения величины угла правильного n-угольника.  , где , где 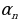 – угол правильного n-угольника. – угол правильного n-угольника.
- Зная формулу нахождения угла правильного n-угольника легко получить значения углов правильного треугольника, четырехугольника, пятиугольника и т.д. Поработайте в парах. Ваша задача – посчитать углы: 1 вариант: а) правильного треугольника; б) правильного шестиугольника; 2 вариант: а) правильного четырехугольника; б) правильного пятиугольника. Затем поменяйтесь тетрадями и проверьте вычисления. - Выполните на скорость в парах задание 1081. Найдите углы правильного n-угольника, если а) n = 3; б) n = 5; в) n = 6; г) n = 10; д) n = 18. Какая теорема поможет решить эту задачу? Запишите эту теорему-формулу.
- В 8 классе Вы изучили теорему о том, что около любого треугольника можно описать окружность, и при том только одну. Правильный треугольник – частный случай треугольника. Однако не только правильные треугольники обладают данным свойством. Оказывается, около любого правильного многоугольника можно описать окружность, и при том только одну. Докажем эту теорему. |
Записывают определение в тетрадь.
- Равносторонний треугольник.
- Все углы равны 60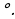 - Высота, медиана и биссектриса, проведенные к каждой из сторон треугольника, совпадают. - Биссектриса, медиана, высота, проведенные к каждой из сторон треугольника, точкой пересечения делятся в отношении 2:1. - В любой треугольник можно вписать окружность, притом только одну. - Около любого треугольника можно описать окружность, притом только одну.
- Да, сумма углов правильного n-угольника равна 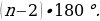
- Всего n углов и все они равны.
- Нужно сумму углов разделить на количество углов n: 
Записывают формулу.
Выполняют подсчеты. Проверяют ответы.
Теорема о величине угла правильного многоугольника. 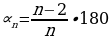
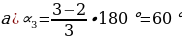
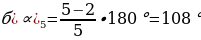
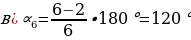
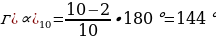
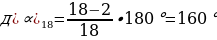
|
| 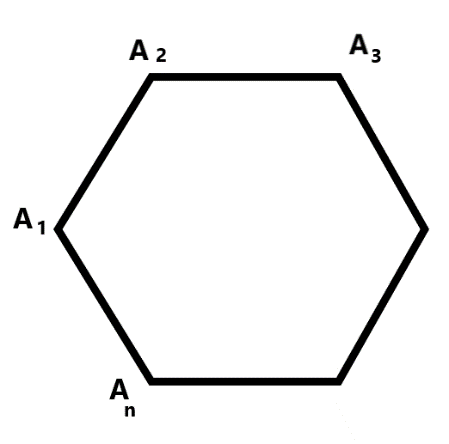 Дано: Дано:
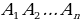 – правильный многоугольник – правильный многоугольник
Доказать: 1) Около 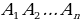 можно описать окружность можно описать окружность 2) Такая окружность единственная Поиск доказательства: - Дополнительное построение 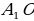 – биссектриса ∠ – биссектриса ∠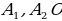 – биссектриса ∠ – биссектриса ∠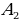 , О= , О=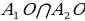 , , 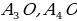 , … , …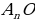 . Что можно сказать об углах правильного многоугольника ∠ . Что можно сказать об углах правильного многоугольника ∠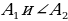 ? ? (Они равны по определению правильного многоугольника) - Что можно сказать о углах ∠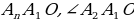 , ∠ , ∠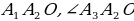 ? ? (Они равны, так как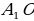 – биссектриса ∠ – биссектриса ∠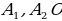 – биссектриса ∠ – биссектриса ∠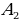 ) ) - Тогда что можно сказать о △ 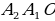 ? ? (Он равнобедренный по признаку равнобедренного треугольника) - Что можно сказать о △ 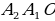 и △ и △ 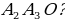 (△ 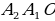 = △ = △ 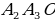 по двум сторонам и углу между ними) по двум сторонам и углу между ними) - Какой вывод можно сделать? (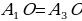 , аналогично, , аналогично, 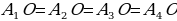 = …= = …=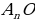 , значит точка О равноудалена от вершин многоугольника. И значит существует окружность с центром в точке О и радиусом , значит точка О равноудалена от вершин многоугольника. И значит существует окружность с центром в точке О и радиусом 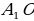 ) ) - Закончено ли доказательство? (Нет, мы не доказали единственность) - Доказывать, что такая окружность только одна, мы будем специальным методом «От противного». Предположим, что есть еще одна такая окружность и докажем, что предположение неверно. Окружность, описанная около многоугольника, проходит через его вершины. Тогда что можно заметить? (Что вершины многоугольника принадлежат обеим окружностям) - Возможно ли это? Почему? (Нет, так как через три точки, не лежащие на одной прямой, проходит окружность, и притом только одна. Значит может быть только одна окружность, описанная около правильного многоугольника) 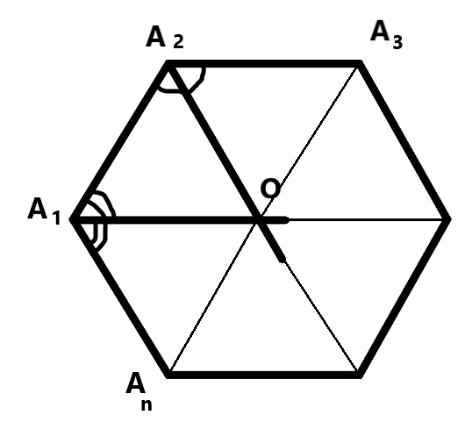 Доказательство: Доказательство:
Дополнительное построение: 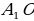 – биссектриса ∠ – биссектриса ∠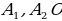 – биссектриса ∠ – биссектриса ∠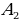
О=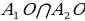 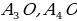 , … , …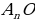
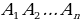 – правильный многоугольник = (по опр. правильного многоугольника) ∠ – правильный многоугольник = (по опр. правильного многоугольника) ∠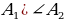
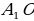 – биссектриса ∠ – биссектриса ∠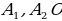 – биссектриса ∠ – биссектриса ∠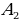 = (по опр. биссектрисы) ∠ = (по опр. биссектрисы) ∠ =∠ =∠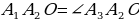
Следовательно, ∠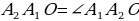 = (по признаку равнобедренного треугольника) △ = (по признаку равнобедренного треугольника) △ 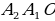 – равнобедренный = (по опр. равнобедренного треугольника) – равнобедренный = (по опр. равнобедренного треугольника) 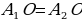 . . Рассмотрим △ 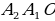 и △ и △ 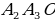 1) 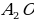 – общая сторона – общая сторона 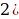 ∠ ∠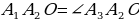 (по опр. биссектрисы (по опр. биссектрисы 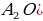
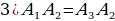 (по опр. правильного многоугольника) (по опр. правильного многоугольника)
Следовательно, △ 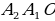 = △ = △ 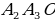 по двум сторонам и углу между ними = по двум сторонам и углу между ними = 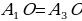 Аналогично, 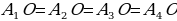 = …= = …=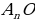 = (по опр. равноудаленной точки) точка О равноудалена от вершин многоугольника = (по опр. равноудаленной точки) точка О равноудалена от вершин многоугольника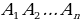 . Следовательно существует окружность с центром в точке О и радиусом . Следовательно существует окружность с центром в точке О и радиусом 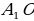 . . Пусть существует еще одна окружность, описанная около многоугольника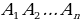 = (по опр. описанной окружности около многоугольника) = (по опр. описанной окружности около многоугольника) 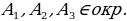 = Получили противоречие с теоремой о том, что через три точки, не лежащие на одной прямой, проходит окружность, и притом только одна = существует только одна окружность, описанная около правильного многоугольника. = Получили противоречие с теоремой о том, что через три точки, не лежащие на одной прямой, проходит окружность, и притом только одна = существует только одна окружность, описанная около правильного многоугольника.
|
| - Сформулируйте данную теорему для правильного а) треугольника, б) четырехугольника, в) пятиугольника.
- И обратите внимание: центр окружности, описанной около правильного многоугольника – это точка пересечения его серединных перпендикуляров. - Кроме того, в любой правильный многоугольник можно вписать окружность, и при том только одну. Докажем эту теорему. | А) Около любого правильного треугольника можно описать окружность, и при том только одну. Б) Около любого правильного четырехугольника можно описать окружность, и при том только одну. В) Около любого правильного пятиугольника можно описать окружность, и при том только одну. |
|  Дано: Дано:
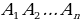 – правильный многоугольник – правильный многоугольник
Доказать: В 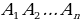 можно вписать окружность можно вписать окружность Такая окружность единственная
Поиск доказательства: - Доказательство этой теоремы похоже на доказательство предыдущей. Поэтому при доказательстве будем опираться на прошлые рассуждения. Что можно сказать о △ 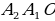 ? ? (Он равнобедренный по признаку равнобедренного треугольника) - Что можно сказать о △ 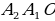 и △ и △ 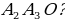 (△ 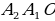 = △ = △ 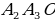 по двум сторонам и углу между ними) по двум сторонам и углу между ними) - Дополнительное построение: О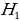 , О , О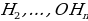 – высоты треугольников соответственно △ – высоты треугольников соответственно △ 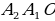 , △ , △ 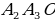 , …, △ , …, △ 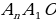 - Какой вывод можно сделать? (О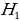 = О = О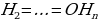 , значит точка О равноудалена от сторон многоугольника. И значит существует окружность с центром в точке О и радиусом О , значит точка О равноудалена от сторон многоугольника. И значит существует окружность с центром в точке О и радиусом О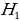 ) ) - Какой шаг доказательства осталось осуществить? (Доказать, что такая окружность единственная) - Как следует доказать единственность? (Методом «От противного». Предположим, что есть еще одна такая окружность и докажем, что предположение неверно) - Тогда что можно заметить? (Обе окружности касаются сторон правильного многоугольника в точках 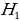 , , 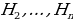 = Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна) = Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна) Доказательство:  1. Дополнительное построение: 1. Дополнительное построение:
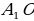 – биссектриса ∠ – биссектриса ∠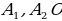 – биссектриса ∠ – биссектриса ∠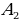
О=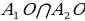 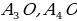 , … , …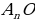
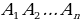 – правильный многоугольник = (по опр. правильного многоугольника) ∠ – правильный многоугольник = (по опр. правильного многоугольника) ∠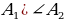
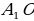 – биссектриса ∠ – биссектриса ∠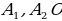 – биссектриса ∠ – биссектриса ∠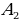 = (по опр. биссектрисы) ∠ = (по опр. биссектрисы) ∠ =∠ =∠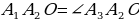
Следовательно, ∠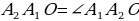 = (по признаку равнобедренного треугольника) △ = (по признаку равнобедренного треугольника) △ 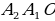 – равнобедренный = (по опр. равнобедренного треугольника) – равнобедренный = (по опр. равнобедренного треугольника) 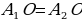 . . 2. Дополнительное построение: О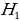 , О , О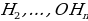 – высоты треугольников соответственно △ – высоты треугольников соответственно △ 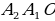 , △ , △ 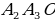 , …, △ , …, △ 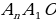 3. Рассмотрим △ 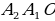 и △ и △ 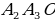 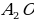 – общая сторона – общая сторона
∠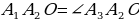 (по опр. биссектрисы (по опр. биссектрисы 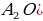 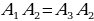 (по опр. правильного многоугольника) (по опр. правильного многоугольника)
Следовательно, △ 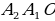 = △ = △ 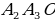 по двум сторонам и углу между ними = О по двум сторонам и углу между ними = О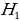 = О = О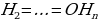 = окружность с центром в точке О и радиусом О = окружность с центром в точке О и радиусом О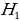 проходит через точки проходит через точки 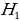 , , 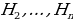 и касается сторон многоугольника в этих точках = (по опр. вписанной окружности) существует окружность с центром в точке О и радиусом и касается сторон многоугольника в этих точках = (по опр. вписанной окружности) существует окружность с центром в точке О и радиусом 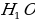 , вписанная в правильный многоугольник. , вписанная в правильный многоугольник. 4. Пусть существует еще одна окружность, вписанная в многоугольник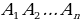 = (по опр. вписанной в многоугольник окружности) окружность касается сторон правильного многоугольника в точках = (по опр. вписанной в многоугольник окружности) окружность касается сторон правильного многоугольника в точках 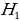 , , 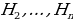 = Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна. = Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна. |
| - Точка пересечения биссектрис является центром вписанной окружности треугольника. Тогда какая точка является центром вписанной окружности правильного многоугольника? - Обратите внимание на доказательство последней теоремы. Какие отрезки являются радиусами вписанной окружности? - Чем еще являются эти высоты в равнобедренных треугольниках △ 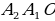 , △ , △ 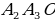 , …, △ , …, △ 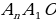 ? ? -Тогда в каких точках вписанная окружность касается правильного многоугольника? - Верно! Вы сформулировали первое следствие из изученных теорем. Запишите его. - Второе следствие говорит о том, что центры вписанной и описанной окружности правильного многоугольника совпадают. Что тогда можно сказать о точках пересечения биссектрис и серединных перпендикуляров? - И эта точка называется центром многоугольника. |
- Точка пересечения биссектрис правильного многоугольника.
- Высоты О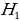 , О , О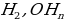 . .
- По свойству равнобедренных треугольников высоты являются еще и медианами. - Окружность, вписанная в правильный многоугольник, касается его сторон в их серединах.
- Они совпадают.
|
| Рефлексивно-оценочная часть |
| - Итак, какова была цель урока?
- Достигли мы цели? - Сформулируйте определение правильного многоугольника.
- По какой формуле находят величину угла правильного n-угольника? - Какие свойства правильного многоугольника Вы изучили сегодня?
| - Изучить понятие правильного многоугольника, его свойства. - Да - Правильным многоугольником называется выпуклый многоугольник, у которого все стороны равны, и все углы равны. -  - Около любого многоугольника можно описать окружность, и притом только одну. - В любой многоугольник можно вписать окружность, и притом только одну. Центры вписанной и описанной окружности совпадают. Это точка называется центром правильного многоугольника. |
| Домашнее задание: пункты 105 – 107 читать, учить записи в тетради, № 1083 |












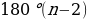 .
.  , где
, где 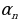 – угол правильного n-угольника.
– угол правильного n-угольника.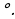
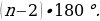
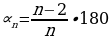
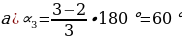
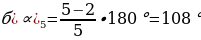
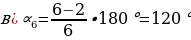
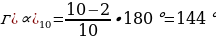
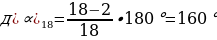
 Дано:
Дано: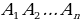 – правильный многоугольник
– правильный многоугольник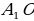 – биссектриса ∠
– биссектриса ∠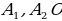 – биссектриса ∠
– биссектриса ∠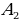 , О=
, О=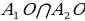 ,
, 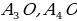 , …
, …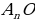 . Что можно сказать об углах правильного многоугольника ∠
. Что можно сказать об углах правильного многоугольника ∠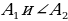 ?
?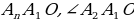 , ∠
, ∠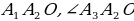 ?
?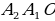 ?
?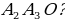
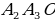 по двум сторонам и углу между ними)
по двум сторонам и углу между ними)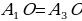 , аналогично,
, аналогично, 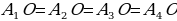 = …=
= …= Доказательство:
Доказательство: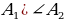
 =∠
=∠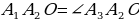
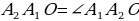 = (по признаку равнобедренного треугольника) △
= (по признаку равнобедренного треугольника) △ 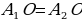 .
. 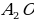 – общая сторона
– общая сторона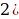 ∠
∠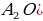
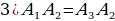 (по опр. правильного многоугольника)
(по опр. правильного многоугольника)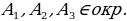 = Получили противоречие с теоремой о том, что через три точки, не лежащие на одной прямой, проходит окружность, и притом только одна = существует только одна окружность, описанная около правильного многоугольника.
= Получили противоречие с теоремой о том, что через три точки, не лежащие на одной прямой, проходит окружность, и притом только одна = существует только одна окружность, описанная около правильного многоугольника.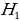 , О
, О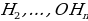 – высоты треугольников соответственно △
– высоты треугольников соответственно △ 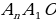
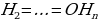 , значит точка О равноудалена от сторон многоугольника. И значит существует окружность с центром в точке О и радиусом О
, значит точка О равноудалена от сторон многоугольника. И значит существует окружность с центром в точке О и радиусом О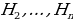 = Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна)
= Но тогда окружности совпали, и окружность, вписанная в правильный многоугольник только одна)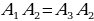 (по опр. правильного многоугольника)
(по опр. правильного многоугольника)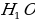 , вписанная в правильный многоугольник.
, вписанная в правильный многоугольник.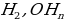 .
.









