Муниципальное бюджетное общеобразовательное учреждение основная общеобразовательная школа с. Зайцево
Урок алгебры в 8 классе.
тема: “Решение неполных квадратных уравнений”
Панкова Ляйсира Винусовна,
учитель математики
Урок алгебры в 8 классе.
тема: “Решение неполных квадратных уравнений”
Панкова Л.В. , учитель математики I квалификационная категория.
Главная дидактическая цель урока: Научить решать неполные квадратные уравнения.
Обучающие цели урока: Сформировать умения в решении неполных квадратных уравнениях:
С помощью вынесения общего множителя за скобки.
С помощь разложения левой части уравнения на множители (Формула сокращенного умножения “Разность квадратов”).
Систематизация знаний по решению неполных квадратных уравнений.
Развивающие цели урока:
Рассказать историческое развитие решения квадратных уравнений.
Показать решение неполных квадратных уравнений геометрическим способом
Воспитывающие цели урока: Вызвать чувство уважения к истории математики и понимание её значения в жизни человека. Создать условия для развития познавательной активности самостоятельности и самооценки.
Тип урока: Закрепление изученного материала
К уроку учащимся было предложено повторить темы: “Формулы сокращенного умножения” и способ вынесения общего множителя за скобки.
Ход урока:
Организационный момент.
Проверка усвоения знаний в форме дидактической игры “найди ошибку” (на доске записаны решения семи уравнениях с ошибками и без ошибок, учащиеся должны найти ошибки и рассказать алгоритм решения уравнения, записать верное решение)
1. 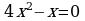 2.
2. 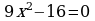 3.
3. 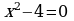 4.
4. 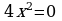
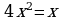
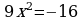
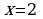
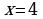
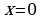

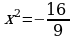
нет решения
5. 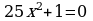 6.
6. 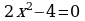 7.
7. 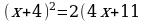
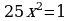
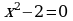
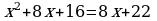
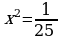
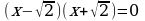
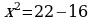
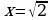
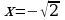
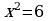
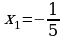
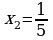
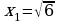
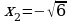
Систематизация знаний. После решения уравнений нахождения ошибок и повторения алгоритмов решения, учащиеся вместе с учителем составляю таблицу:
| Вид уравнения | Метод решения | Число решений | Нахождение корня |
| 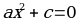
| Разложить по формуле разность квадратов, левую часть уравнения. | Два решения если cc0 | 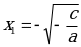 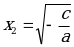
|
| 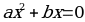
| Вынесение общего множителя x за скобки. | Два решения |  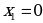
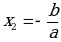
|
| 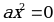
| Множитель x=0 | Одно решение | 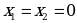
|
Знакомство с историческим материалом. Читает один из учеников по просьбе учителя (смотри приложение)
Опережающее обучение. Учитель показывает и поясняет графический способ решения неполных квадратных уравнений.

X
Y


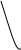
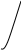
X
Y

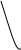
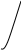
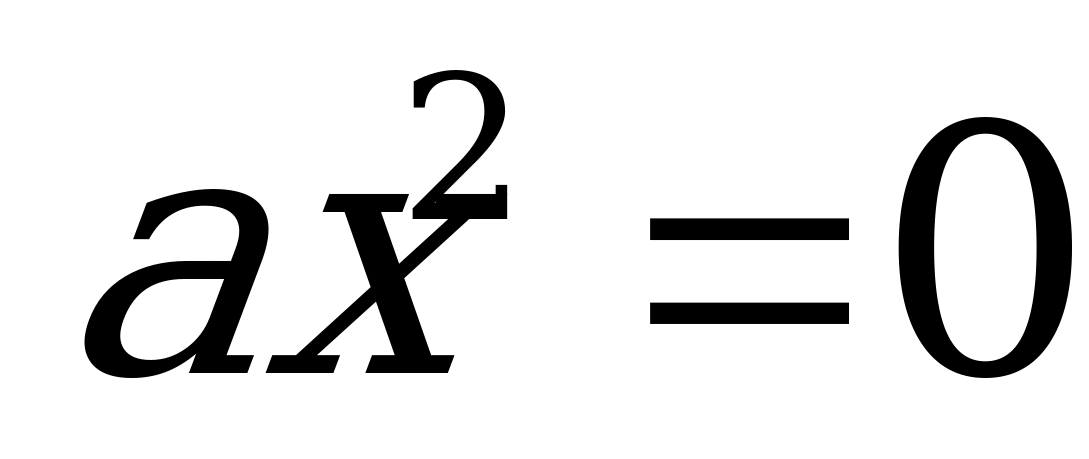
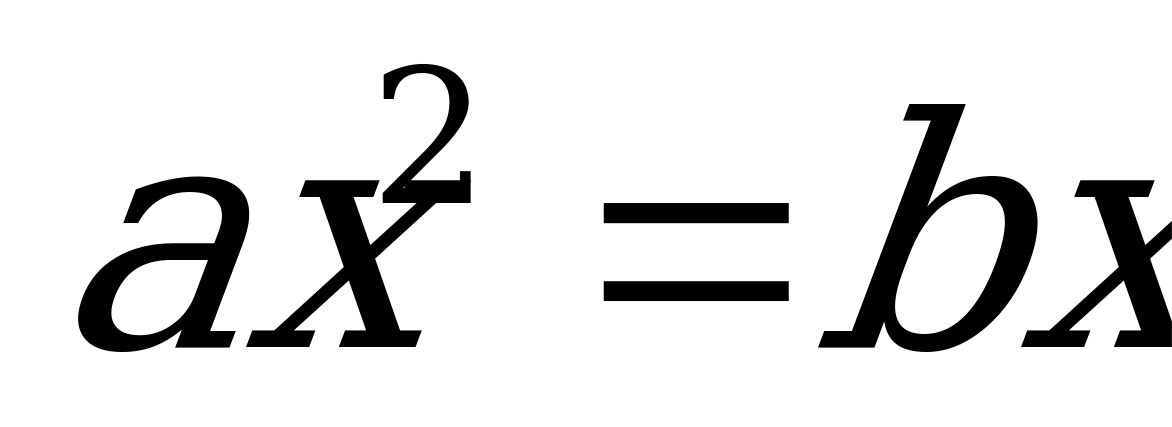
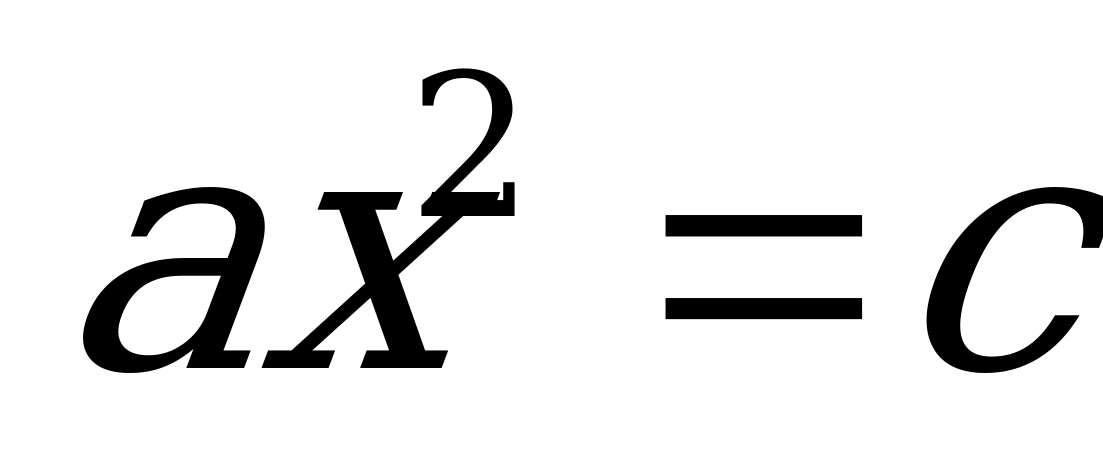
Error: Reference source not found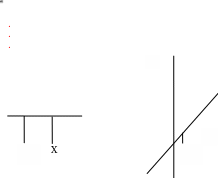
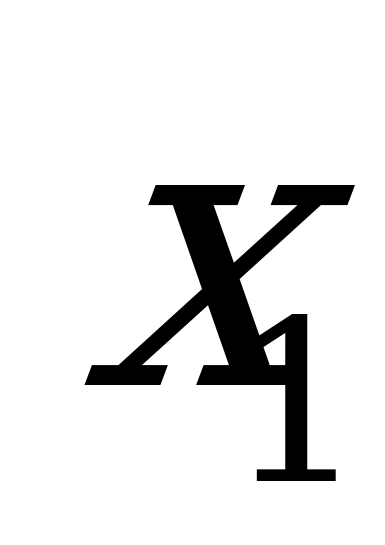
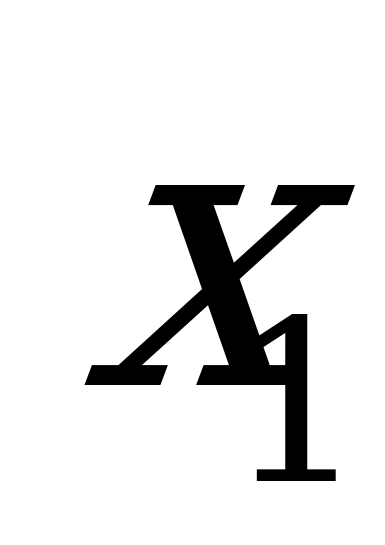
Закрепление полученных знаний на практике осуществляется в виде трёхуровневой обучающей самостоятельной работы, где учащихся сами определяют для себя уровень
Самостоятельная работа:
I уровень (обязательный) II уровень (средний) III уровень (повышенный)
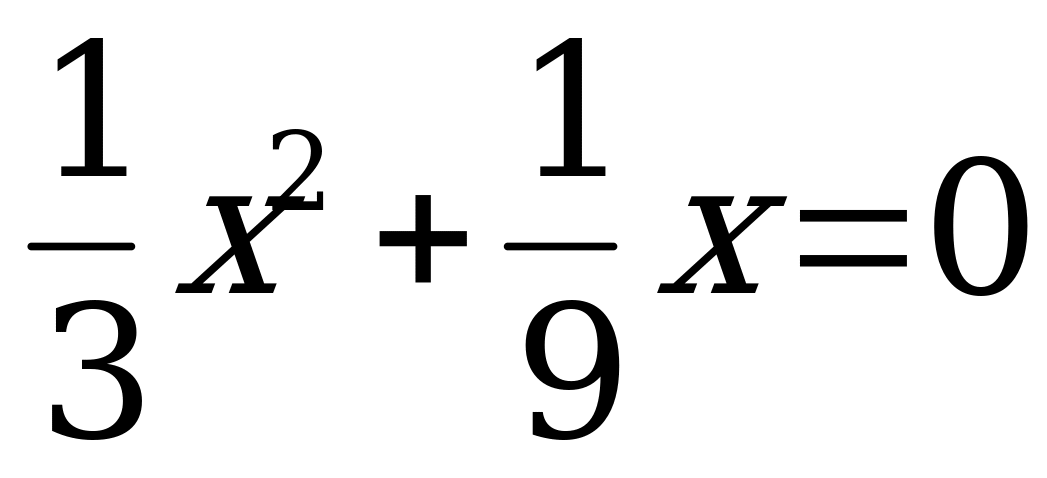
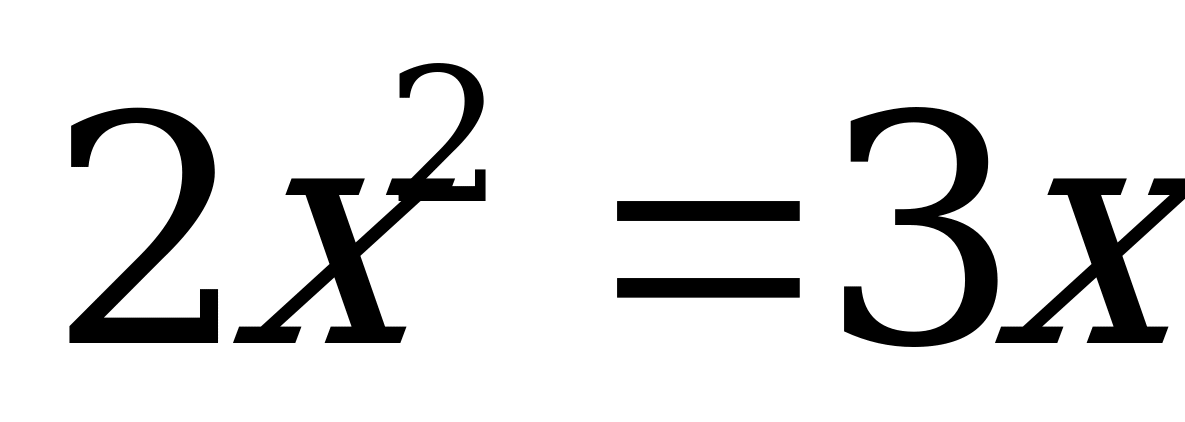
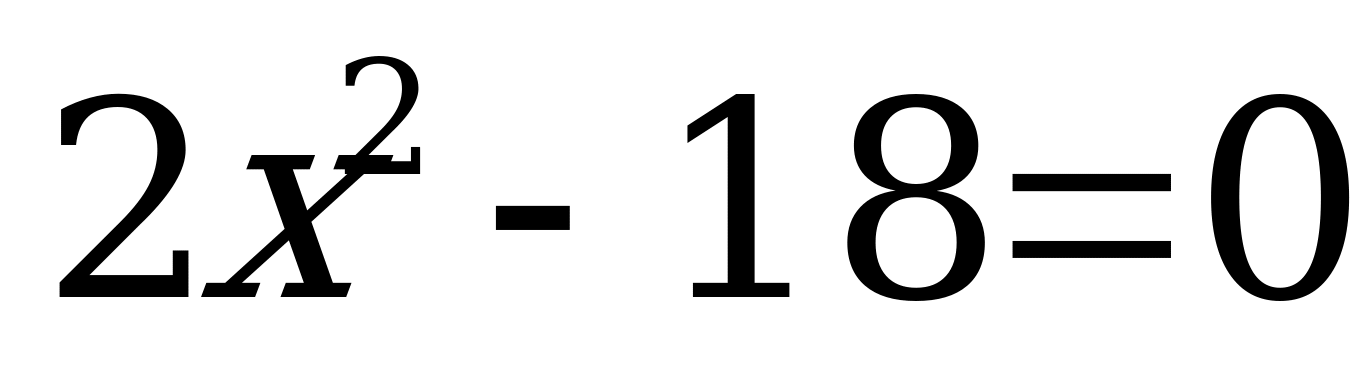
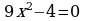
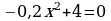
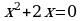
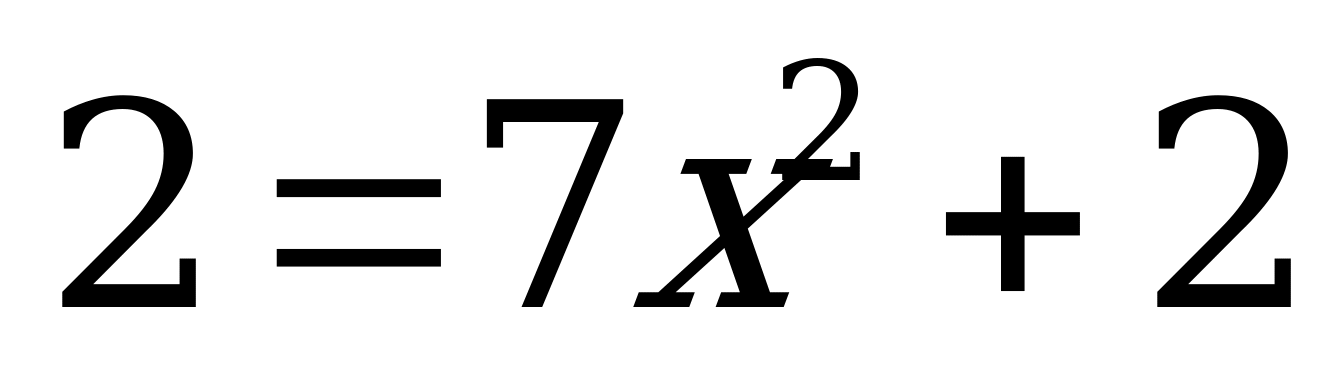
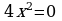
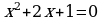
 При каком a один из
При каком a один из 
корней уравнения При каком значении a
равен 1? корни уравнения
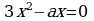 являются противо-
являются противо-
ложными числами
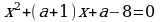
Подведение итогов:
После окончания самостоятельной работы, обучающиеся вместе с учителем разбирают задания повышенной сложности, которые вызвали наибольший интерес. На скрытой части доски после решения самостоятельной работы учитель представляет ответы и частичное решение уравнений, учащиеся могут оценить результат своей работы.
В качестве домашнего задания учитель предлагает разноуровневые задания.
Уровень:
a) 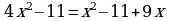
b) 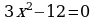
c) 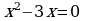
d) 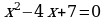
Уровень:
a) 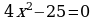
b) 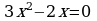
c) 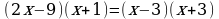
d) 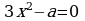 При каком a один из корней уравнения равен 1?
При каком a один из корней уравнения равен 1?
Уровень:
a) 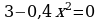
b) 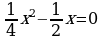
c) 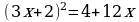
d) 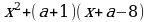 При каком значении a корни уравнения являются противоположными числами?
При каком значении a корни уравнения являются противоположными числами?
Приложение:
Историческая справка.
Неполные квадратные уравнения и частные виды полных квадратных уравнений умели решать вавилоняне около двух тысяч лет до нашей эры. Об этом свидетельствует найденные клинописные тексты задач с решениями в виде рецептов. Некоторые виды квадратных уравнений, сводя их решения к геометрическим построениям могли решать древнегреческие математики. Приёмы решения уравнений без обращения к геометрии даёт Диофант Александрийский (III век), дошедших до нас 6 из 13 книг арифметика содержаться задачи с решениями, в которых Диофант объясняет, как надо выбрать неизвестное, чтобы получит решение уравнения вида: 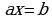 и
и 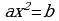 . Способ решения полных квадратных уравнений Диофант изложил в книгах “арифметика” которые не сохранились. Правила решения неполных квадратных уравнений дал индийский учёный Брахмагупта, а хорезмский математик Аль Хорезми разъясняет решение неполных квадратных уравнений и отыскивает только положительные корни. Общее правило решения квадратных уравнений было сформулировано немецким математиком М Штифелем. 1487-1567. Выводом формулы решения квадратных уравнений общего вида занимался Виетт, однако своё утверждении он высказывал лишь для положительных корней. Формулы, выражающие зависимость корней уравнения от его коэффициента были выведены Виетом в 1591 году.
. Способ решения полных квадратных уравнений Диофант изложил в книгах “арифметика” которые не сохранились. Правила решения неполных квадратных уравнений дал индийский учёный Брахмагупта, а хорезмский математик Аль Хорезми разъясняет решение неполных квадратных уравнений и отыскивает только положительные корни. Общее правило решения квадратных уравнений было сформулировано немецким математиком М Штифелем. 1487-1567. Выводом формулы решения квадратных уравнений общего вида занимался Виетт, однако своё утверждении он высказывал лишь для положительных корней. Формулы, выражающие зависимость корней уравнения от его коэффициента были выведены Виетом в 1591 году.
5






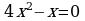 2.
2. 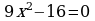 3.
3. 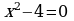 4.
4. 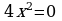
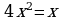
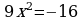
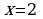
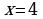
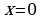

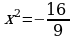
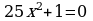 6.
6. 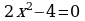 7.
7. 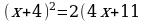
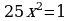
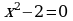
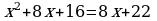
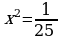
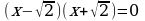
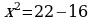
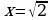
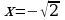
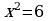
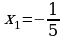
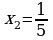
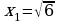
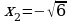


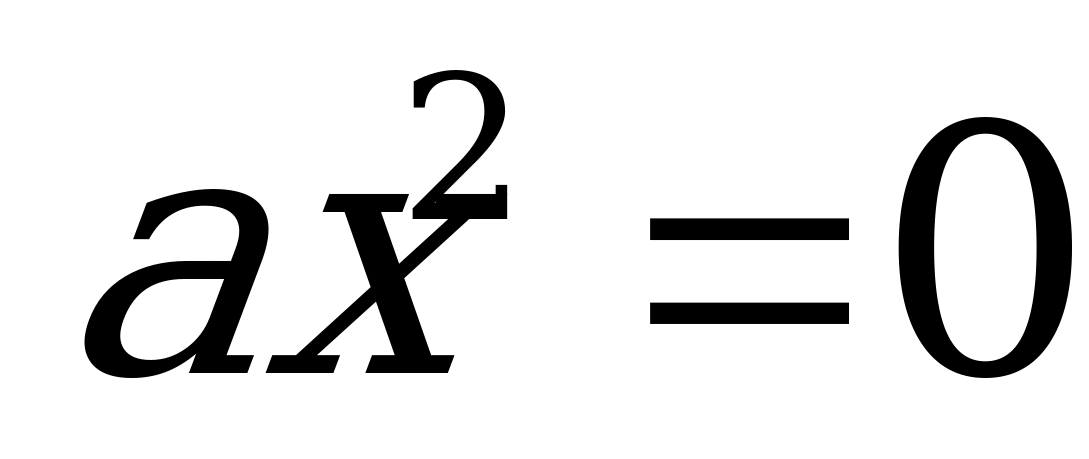
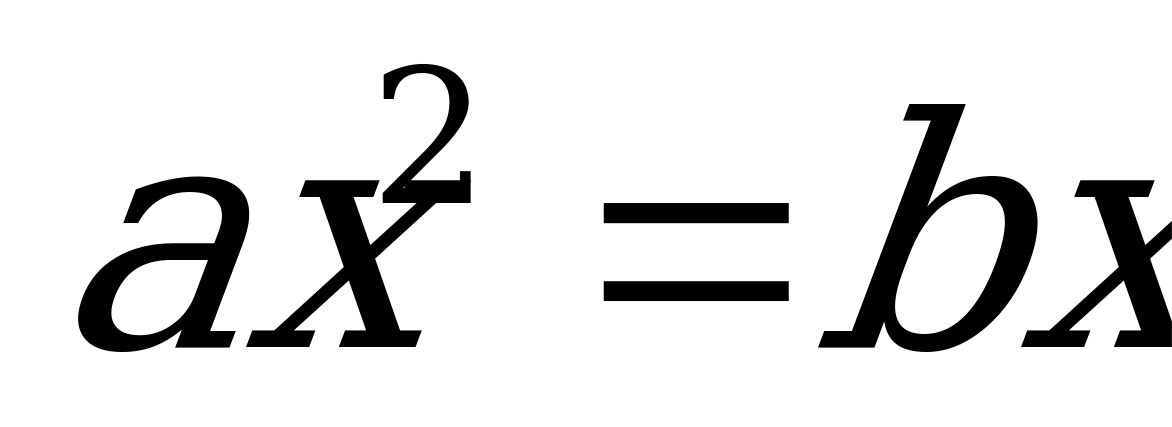
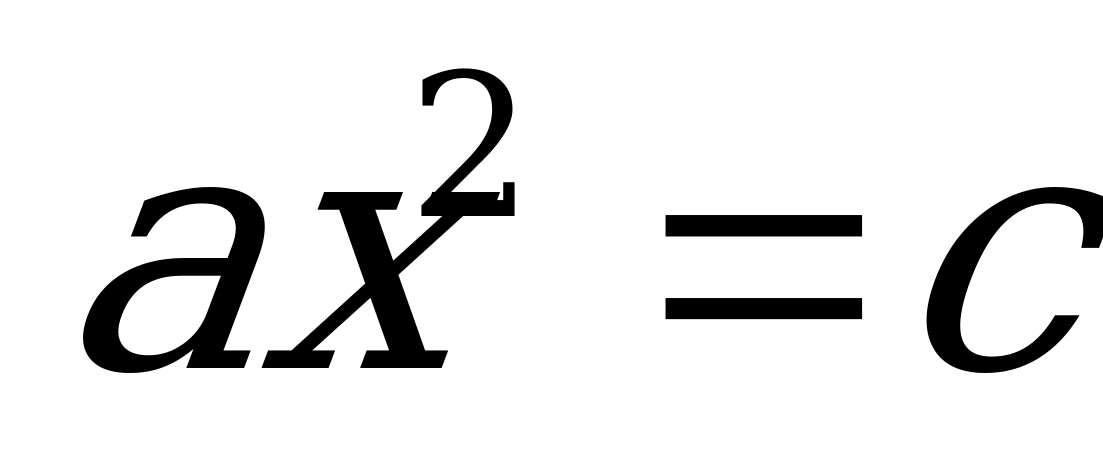

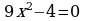
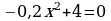
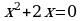
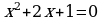
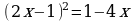
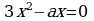 являются противо-
являются противо-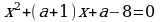
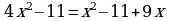
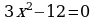
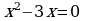
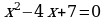
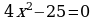
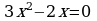
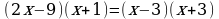
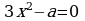 При каком a один из корней уравнения равен 1?
При каком a один из корней уравнения равен 1?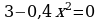
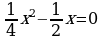
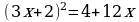
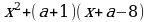 При каком значении a корни уравнения являются противоположными числами?
При каком значении a корни уравнения являются противоположными числами?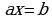 и
и 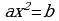 . Способ решения полных квадратных уравнений Диофант изложил в книгах “арифметика” которые не сохранились. Правила решения неполных квадратных уравнений дал индийский учёный Брахмагупта, а хорезмский математик Аль Хорезми разъясняет решение неполных квадратных уравнений и отыскивает только положительные корни. Общее правило решения квадратных уравнений было сформулировано немецким математиком М Штифелем. 1487-1567. Выводом формулы решения квадратных уравнений общего вида занимался Виетт, однако своё утверждении он высказывал лишь для положительных корней. Формулы, выражающие зависимость корней уравнения от его коэффициента были выведены Виетом в 1591 году.
. Способ решения полных квадратных уравнений Диофант изложил в книгах “арифметика” которые не сохранились. Правила решения неполных квадратных уравнений дал индийский учёный Брахмагупта, а хорезмский математик Аль Хорезми разъясняет решение неполных квадратных уравнений и отыскивает только положительные корни. Общее правило решения квадратных уравнений было сформулировано немецким математиком М Штифелем. 1487-1567. Выводом формулы решения квадратных уравнений общего вида занимался Виетт, однако своё утверждении он высказывал лишь для положительных корней. Формулы, выражающие зависимость корней уравнения от его коэффициента были выведены Виетом в 1591 году.









