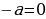Конспект урока по теме «Уравнения, неравенства и их системы»
Урок «Решение квадратных уравнений с параметром» 8 класс
Тип урока: введение нового материала.
Актуализация опорных знаний.
Форма работы: фронтальная.
Учитель: назовите общий вид квадратного уравнения.
Ученик: ах2+bх+с=0,где х-переменная, а, b, с-некоторые числа, причем а≠0.
Учитель: какое уравнение называют неполным квадратным уравнением?
Ученик: если в квадратном уравнении ах2+bх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называют неполным квадратным уравнением.
Учитель: Рассмотрим следующее задание. При каких значениях а уравнение является квадратным? Назовите это уравнение.
а) (а-1)x3+3ax2+2x-5a=0
Ученик: при а=1 уравнение является квадратным. Квадратное уравнение 3х2+2х-5=0.
б) (2а+4)x3-2ах2+ах-7=0.
Ученик: при а=-2 уравнение является квадратным. Квадратное уравнение 4х2-2х-7=0.
в) (2а-4)x3-(а-2)х2+ах-3=0.
Ученик: ни при каких а уравнение является квадратным.
Учитель: при каком значении а один из корней уравнения ах2-3х-5=0 равен 1?
Ученик: а∙12-3∙1-5=0, а-3-5=0, а=8. Ответ: при а=8 один из корней уравнения ах2-3х-5=0 равен 1.
Учитель: при каких значениях а уравнение 2х2-(а-3)х-5а=0 является неполным квадратным? Назовите это уравнение.
Ученик: 1) при а =3 уравнение 2х2-(а-3)х-5а=0 является неполным квадратным; неполное квадратное уравнение 2х2-15=0. 2) при а=0 уравнение 2х2-(а-3)х-5а=0 является неполным квадратным; неполное квадратное уравнение2х2+3х=0.
Изучение нового материала.
Учитель: Прочитайте определение «Что значит решить уравнение с параметром».
Ученик: решить уравнение с параметром – это значит показать, каким образом для любого значения параметра можно найти соответствующее множество корней уравнения, если корни существуют, или установить, что при этом значении параметра корней нет.
(прошу одного из учеников воспроизвести определение). Чувствуете трудность?
Ученик: да.
Учитель: тогда познакомимся с решением уравнений с параметром на практике.
Перейдем к следующему заданию. Решите квадратное уравнение
ах2+(1-а)х -1=0.
Всегда ли это уравнение квадратное?
Ученик: Нет. Если а=0, то уравнение линейное: х -1=0; его корень х=1.
Если а≠0, то уравнение квадратное.
Учитель: Найдите дискриминант уравнения, если а≠0.
D=b2-4ас
D=(1-a)2-4a(-1)
D=1-2а+а2 +4а
D=а2 +2а+1
а) D=(a+1)2 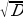 =
=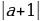 , если a=-1, то D=0 и квадратное уравнение
, если a=-1, то D=0 и квадратное уравнение
б) ах2+(1-а)х -1=0 имеет 1 корень. Если a≠-1, то D0 и квадратное уравнение в) ах2+(1-а)х -1=0 имеет 2 корня. Выражение (a+1)2 всегда ≥0, поэтому D
Учитель: Примените формулу корней квадратного уравнения и найдите корни квадратного уравнения при a≠-1.
х= 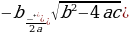 х=
х=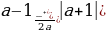
х1=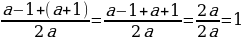 . х2=
. х2=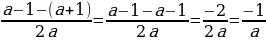 .
.
Примените формулу корней квадратного уравнения и найдите корни квадратного уравнения при a=-1.
x=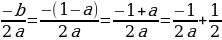
Учитель: Запишите ответ.
Ответ: 1. Если а≠0: 1) a≠-1, то х1=1; х2=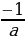 . 2)a=-1, то x=
. 2)a=-1, то x=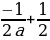 .
.
2. Если а=0, то х=1.
х2-(2а+1)х+а2+а-2=0.
Всегда ли это уравнение квадратное?
Ученик: Да, это уравнение всегда квадратное.
Учитель: Найдите дискриминант уравнения.
D=b2-4ас
D=(-2a-1)2-4а2-4а+8
D=4а2+4а+1-4а2-4а+8
D=9 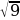 =3
=3
Учитель: Примените формулу корней квадратного уравнения.
х= 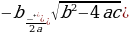 х=
х=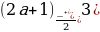
х=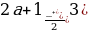
х1=а+2; х2=а-1.
Учитель: Запишите ответ.
Ответ: х1=а+2; х2=а-1.
Учитель: Перейдем к следующему заданию. Решите уравнение:
х2-(2а+1)х+а2+а-2=0.
Для любого ли a уравнение является квадратным?
Ученик: Да, это уравнение всегда квадратное.
Учитель: Найдите дискриминант уравнения.
D=b2-4ас
D=(-2a-1)2-4а2-4а+8
D=4а2+4а+1-4а2-4а+8
D=9 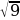 =3
=3
Учитель: Примените формулу корней квадратного уравнения.
х= 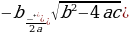 х=
х=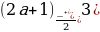
х=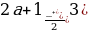
х1=а+2; х2=а-1.
Учитель: Запишите ответ.
Ответ: х1=а+2; х2=а-1.
Учитель: Рассмотрим алгоритм решения «квадратного» уравнения с параметром:
1.Найти значения параметра a, при которых уравнение не является квадратным (коэффициент при х2=0).
2.Решить уравнение при этих значениях параметра a.
3.Решить квадратное уравнение относительно x: выразить дискриминант через a и найти значения, при которых D0, DD=0.
4.Выразить корни уравнения при всех значениях параметра a. (D0, DD=0)
Закрепление изученного материала.
Учитель: Перейдем к закреплению каждого шага алгоритма на практике. Читаем задание. Найдите значение параметра, при которых уравнение не является квадратным?
а) (a-2)х2+х +4=0.
Ученик: a-2=0; a=2
б) (3-2a)х2+х -7=0.
Ученик: 3-2a=0; -2a=-3; a=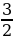
в) (4- 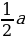 )х2+х +3=0.
)х2+х +3=0.
Ученик: 4- 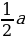 =0; -
=0; - 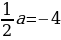 ; a=8
; a=8
Учитель: Перейдем к следующему шагу алгоритма и упражнениям на его закрепление. Выполните задание: Решите уравнение.
а) (a-2)х2+х +4=0.
Ученик: (2-2)х2+х +4=0; х +4=0; x=-4
б) (3-2a)х2+х -7=0.
Ученик: (3-2∙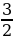 )х2+х -7=0; x-7=0; x=7
)х2+х -7=0; x-7=0; x=7
в) (4- 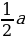 )х2+х +3=0.
)х2+х +3=0.
Ученик: (4- 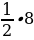 )х2+х +3=0; х +3=0; x=-3
)х2+х +3=0; х +3=0; x=-3
Учитель: Перейдем к следующему шагу алгоритма. Выполните задание: Выразить дискриминант квадратного уравнения. Найти значения a, при которых D0, DD=0.
а) ах2+(2-а)х -1=0
Ученик: 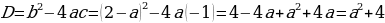
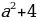 0; a
0; a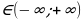
б) (a-1)х2+(3-а)х -3=0
Ученик: 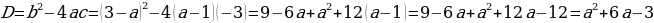
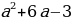 =0; D=48; a1=
=0; D=48; a1=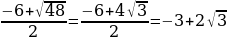 ; a2=
; a2=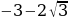 ;
;
D0 при a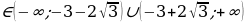 . Dпри a
. Dпри a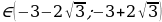 . D=0 при a=
. D=0 при a=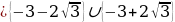
в) (1-2a)х2+(1-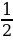 а)х +2=0
а)х +2=0
Ученик: 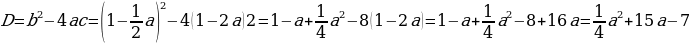
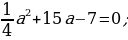 D=232; a1=
D=232; a1=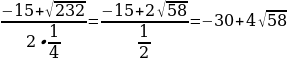 ; a2=
; a2=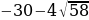
D0 при a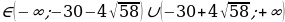 . Dпри a
. Dпри a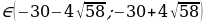 . D=0 при a=
. D=0 при a=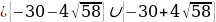
Учитель: Перейдем к последнему шагу алгоритма. Выполните задание: Выразить корни квадратного уравнения, если известен дискриминант этого уравнения.
(-a+1)х2-aх -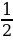 =0; D=(a-1)2=
=0; D=(a-1)2=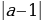
Ученик: а) Если a=1, то D=0, уравнение имеет 1 корень.
б) Если a≠1, то D0, уравнение имеет 2 корня.
в) (a-1)2D
а) x=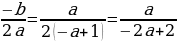
б) х= 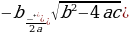 ; х=
; х=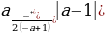 ; х1=
; х1=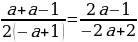 ; x2=
; x2=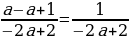
(a+2)х2-4х +2=0; D=-8a
Ученик: а) Если a=0, то D=0, уравнение имеет 1 корень.
б) Если -8a0, aD0, уравнение имеет 2 корня.
в) Если -8aa0, то D
а) x=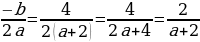
б) х= 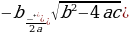 ; х=
; х=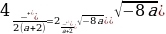 ; х1=
; х1=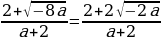 ; x2=
; x2=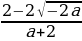 ;
;
(1-a)х2-2х -1=0; D=8-4a
Ученик: а) Если a=2, то D=0, уравнение имеет 1 корень.
б) Если 8-4a0, -4a-8, aD0, уравнение имеет 2 корня.
в) Если 8-4aaa2, то D
а) x=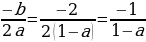
б) х= 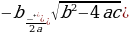 ; х=
; х=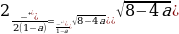 ; х1=
; х1=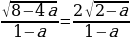 ; x2=
; x2=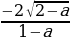
Учитель: Итак, повторим алгоритм решения квадратных уравнений с параметром.
Ученик:
1.Найти значения параметра a, при которых уравнение не является квадратным (коэффициент при х2=0).
2.Решить уравнение при этих значениях параметра a.
3.Решить квадратное уравнение относительно x: выразить дискриминант через a и найти значения, при которых D0, DD=0.
4.Выразить корни уравнения при всех значениях параметра a. (D0, DD=0)
Закрепление шагов алгоритма.
Учитель: Решите квадратное уравнение с параметром.
1. (a-3)х2+х -2=0
2. (a2-5)x2-(a-4)x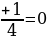
3. (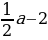 )x2-(a-1)x
)x2-(a-1)x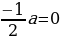
Учитель: Запишем домашнее задание.
(a-5)х2+х -2=0
(a2-5)x2-(2a-5)x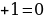
(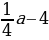 )x2-(2a-1)x
)x2-(2a-1)x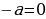







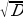 =
=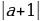 , если a=-1, то D=0 и квадратное уравнение
, если a=-1, то D=0 и квадратное уравнение 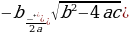 х=
х=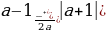
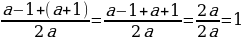 . х2=
. х2=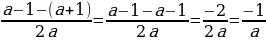 .
.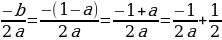
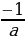 . 2)a=-1, то x=
. 2)a=-1, то x=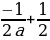 .
. 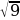 =3
=3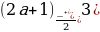
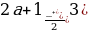
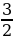
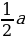 )х2+х +3=0.
)х2+х +3=0.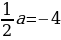 ; a=8
; a=8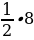 )х2+х +3=0; х +3=0; x=-3
)х2+х +3=0; х +3=0; x=-3 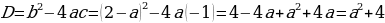
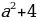 0; a
0; a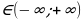
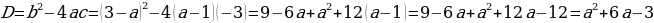
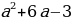 =0; D=48; a1=
=0; D=48; a1=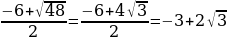 ; a2=
; a2=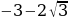 ;
; 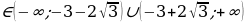 . Dпри a
. Dпри a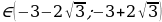 . D=0 при a=
. D=0 при a=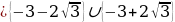
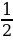 а)х +2=0
а)х +2=0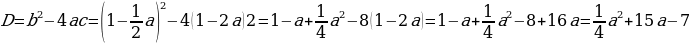
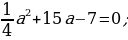 D=232; a1=
D=232; a1=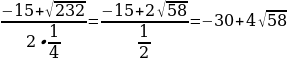 ; a2=
; a2=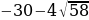
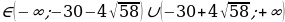 . Dпри a
. Dпри a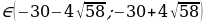 . D=0 при a=
. D=0 при a=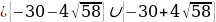
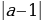
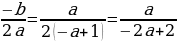
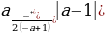 ; х1=
; х1=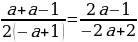 ; x2=
; x2=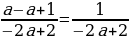
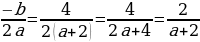
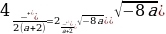 ; х1=
; х1=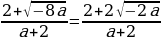 ; x2=
; x2=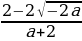 ;
; 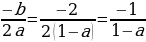
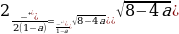 ; х1=
; х1=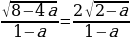 ; x2=
; x2=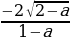
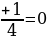
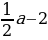 )x2-(a-1)x
)x2-(a-1)x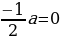
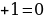
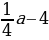 )x2-(2a-1)x
)x2-(2a-1)x