Предмет: Алгебра
Тема: Графический способ решения систем уравнений. 9-й класс
Класс: 9 класс
Педагог: Улицкая Ю.И.
Тип урока: урок изучения нового материала.
Цель урока:
дидактические:
открыть совместно с учащимися новый способ решения систем уравнений;
вывести алгоритм решения систем уравнений графическим способом;
уметь определять сколько решений имеет система уравнений;
учить находить решения системы уравнений графическим способом;
повторить построение графиков элементарных функций;
создать условия для контроля (самоконтроля) учащихся:
воспитательные:
воспитание ответственного отношения к труду,
аккуратности ведения записей.
Ход урока.
I. Организационный момент.
II. Повторение.
Что такое функция?
Что называется графиком функции?
Какие виды функций вы знаете?
Какой формулой задается линейная функция? Что является графиком линейной функции?
Какой формулой задается прямая пропорциональность? Что является ее графиком?
Какой формулой задается обратная пропорциональность? Что является ее графиком?
Какой формулой задается квадратичная функция? Что является ее графиком?
Каким уравнением задается уравнение окружности?
Что называют графиком уравнения с двумя переменными;)
Организуется знакомство с уравнениями, используемыми в высшей математике и их графиками (строфоидой, Лемнискатой Бернулли, астроидой, кардиоидой).
Рассказ учителя сопровождается показом слайдов с данными графиками.
Выразите переменную у через переменную х:
а) у – х² = 0
б) х + у + 2 = 0
в) 2х – у + 3 = 0
г) ху = -12
Является ли пара чисел (1; 0) решением уравнения
а) х² +у = 1;
б) ху + 3 = х;
в) у(х +2) = 0.
Что является решением системы уравнений с двумя переменными?
Какая из пар чисел является решением системы уравнений 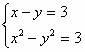
а) (6; 3)
б) (- 3; - 6)
в) (2; - 1)
г) (3; 0)
Из каких уравнений можно составить систему уравнений, решением которой будет пара чисел (2; 1)
а) 2х – у = 3
б) 3х – 2у = 5
в) х² + у² = 4
г) ху = 2
III. Актуализация знаний учащихся по изученному материалу
Сегодня мы повторим и закрепим один из способов решения систем уравнений. Закрепление изученного материала осуществляется с помощью наглядного восприятия (на слайде представлено графическое решение системы уравнений):

Графиком уравнения с двумя переменными называется множество точек координатной плоскости, координаты которых обращают уравнение в верное равенство. Графики уравнений с двумя неизвестными весьма разнообразны.
Вопросы по данному слайду:
Что является графиком уравнения x² + y²=25?
Что является графиком уравнения y = - x² +2x +5?
Координаты любой точки окружности будут удовлетворять уравнению x² + y²=25, координаты любой точки параболы будут удовлетворять уравнению y = - x² +2x +5.
Координаты каких точек будут удовлетворять и первому и второму уравнениям?
Сколько точек пересечения у данных графиков?
Сколько решений имеет данная система?
Назвать эти решения?
Что нужно сделать, чтобы графически решить систему уравнений с двумя переменными?
Предлагается слайд, на котором приведен алгоритм графического способа решения систем уравнений с двумя неизвестными.
Графический способ применим к решению любой системы, но с помощью графиков уравнений можно приближенно находить решения системы. Лишь некоторые найденные решения системы могут оказаться точными. В этом можно убедиться, подставив их координаты в уравнения системы.
IV. Применение изученного способа решения систем уравнений.
1. Решить графически систему уравнений

Постановка наводящих вопросов:
Что является графиком уравнения ху = 3?
Что является графиком уравнения 3х – у =0?
Сколько точек пересечения имеют данные графики?
Сколько решений имеет данная система уравнений?
Назвать решения данной системы уравнений?
2. Запишите систему, определяемую этими уравнениями и ее решение.

Постановка наводящих вопросов:
Запишите систему, определяемую данными уравнениями?
Сколько точек пересечения имеют данные графики?
Сколько решений имеет данная система уравнений?
Назвать решения данной системы уравнений?
3. Выполнение задание из ОГЭ
4. Решить графически систему уравнений
а)  б)
б) 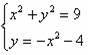
Задание выполняется учащимися в тетрадях. Решение проверяется.
5. Тест.
V. Итоги урока.
Что называется решением системы уравнений с двумя переменными?
С каким способом решения систем уравнений с двумя переменными вы познакомились?
В чём его суть?
Дает ли данный способ точные результаты?
В каком случае система уравнений не будет иметь решений?
VI . Домашнее задание.
П. 11, № 11.33-11.36






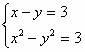

 б)
б)