В честь окончания учебного года! Скидки до 50% на готовые материалы для учителей на каждый урок

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 11.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 18.05.2025 10:16

Науменко Вера Владимировна

учитель математики

29 лет

718

75 463

Подписчики

Подписки

Местоположение

Россия, Благовещенск

Специализация

Математика

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

Конспект урока по геометрии на тему: " Определение подобных треугольников"

Категория: Геометрия

07.04.2021 14:18

Учебник: Геометрия. 7-9 классы. Учебник. Атанасян Л.С. и др. (2014, 384с.)

Тема: Определение подобных треугольников — 137

Просмотр содержимого документа
«Конспект урока по геометрии на тему: " Определение подобных треугольников"»

Пояснительная записка

Геометрия 8 класс. Программная тема «Подобные треугольники». Тема данного урока «Определение подобных треугольников». Это первый пункт программной темы. Тип урока «Изучение нового материала». Тема вводится при использовании учебника Атанасяна Л.С. М. Просвещение, 20-е изд. – 2010 г. и др.
Цели урока:

Образовательная цель: формирование понятия подобные треугольники.

Задачи:

Ввести понятие подобные треугольники.
Сформулировать определение пропорциональных отрезков.
Отрабатывать навыки решения задач с использованием подобия треугольников.

Развивающая цель: развитие памяти, логического мышления, математической речи.

Задачи:

Развивать память учащихся при повторении пройденного материала.
Развивать логическое мышление при решении математических задач.
Развивать познавательный интерес при решении задач.

Воспитательная цель: Воспитание нравственных качеств личности учащихся.

Задачи:

Воспитывать чувства уважительного отношения к ответам одноклассников.
Способствовать самостоятельному принятию решений в ходе урока.
Требовать соблюдения чистоты и порядка в классе, аккуратности ведения записей, поддержания дисциплины в классе.

ЗУН, необходимые на уроке:

знания определение пропорции, основное свойство пропорции.
умения пользоваться ранее полученными знаниями при изучении темы «Подобные треугольники».

ЗУН, формируемые на уроке:

знание определения подобных треугольников,
навыки выполнения упражнений по данной теме.

Средства обучения, использованные на уроке:

мультимедийный проектор,
экран,
компьютер.

Методы обучения:

Метод введения понятия «Подобные треугольники» - конкретно-индуктивный;
Синтез и анализ при решении задач;
Объяснительно – иллюстративный метод при изучении темы «Определение подобных треугольников».

Пути активизации учебной деятельности:

Использование наглядности;
Словесное поощрение;
Создание эмоциональной атмосферы на уроке.

Структура урока:

Организационный момент (1-2 мин)
Повторение (8-10 мин)
Объяснение нового материала (10-12 мин)
Первичное закрепление (10-12 мин)
Постановка домашнего задания (1-2 мин)
Подведение итогов урока (3-4 мин)

Ход урока

Деятельность учителя	Деятельность учащихся
Организационный момент
Здравствуйте, ребята! Присаживайтесь. Кто сегодня отсутствует на уроке?	Приветствуют учителя. Называют отсутствующих.
Повторение
Прежде чем мы начнем изучение новой темы давайте немного повторим. Итак, на слайде представлена запись. Как называются данные числа? Всё верно, это дроби. Так же, данные дроби можно и по-другому назвать – отношение. Т.е. 1 относится к 2, 5 относится к 7 и т.д. Прочтите запись . Как называется данное равенство двух отношений? Верно. А теперь сформулируйте мне основное свойство пропорции. Молодцы! Всё верно.	Отвечают: дроби Отвечают: пропорция. Отвечают: Произведение крайних членов пропорции равно произведению ее средних членов
Объяснение нового материала
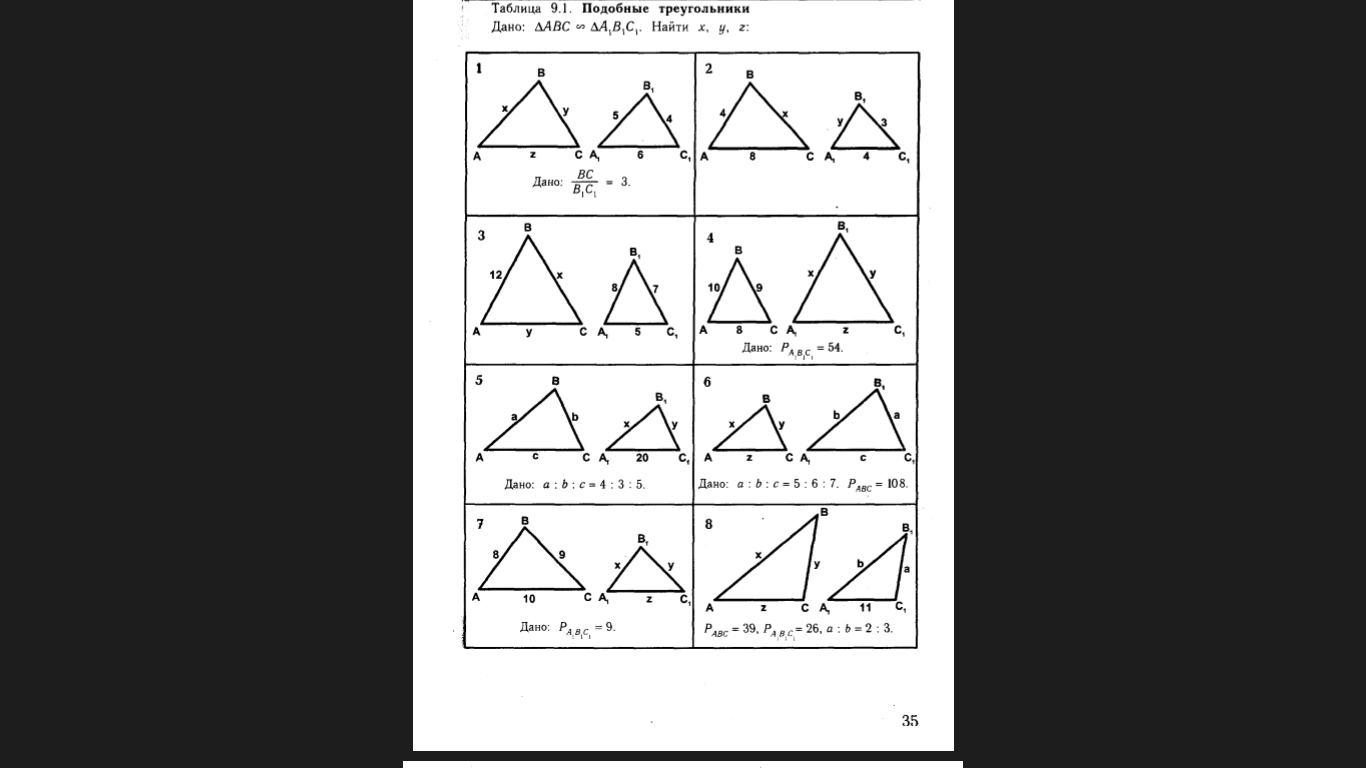
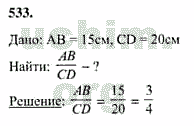Итак, у вас на партах лежит карточка, на ней изображены отрезки AB, CD и MN, PK. Измерьте, пожалуйста, длины данных отрезков и запишите отношение AB:CD и MN:PK. Что вы можете сказать об этих отношениях? Верно, они равны. А из этого следует, что данные отрезки пропорциональны. Запишите, пожалуйста, тему нашего урока «Пропорциональные отрезки. Определение подобных треугольников». Отношением отрезков AB и VN называется отношение их длин. Рассмотрим два отрезка AB и VN, где отрезок АВ в 2 раза больше второго отрезка: 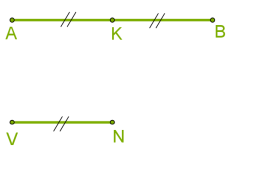Отношение отрезков AB и VN равно 2:1: AB:VN=2:1 Можно также сказать, что отношение отрезков VN и AB равно 1:2: VN:AB=1:2 Задание. Построить два отрезка у которых отношение равно 3:2 В этом примере отрезок AR равен трём единицам, а VZ равен двум единицам. Скажите, а какой длины можно выбрать отрезки, чтобы их отношение было равно 3:2? Верно. 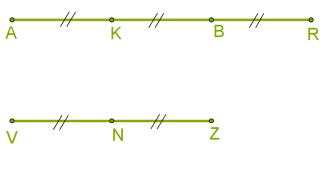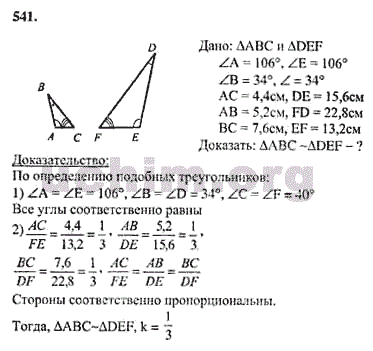Отношение отрезков AR и VZ равно 3:2: AR:VZ=3:2 или VZ:AR=2:3 Теперь запишите определение в тетрадь Определение. Если 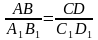, то эти отрезки - пропорциональные. Сравниваем данные ранее отрезки, они не пропорциональны, т.к. AB:VN≠AR:VZ Вывод. Чтобы записать отношение отрезков, необходимо два отрезка. Чтобы найти пропорциональные отрезки, необходимо две пары отрезков. Далее обратите внимание на треугольники, которые лежат у вас на столе. Что вы можете сказать о них? Да, верно, они разных размеров. А теперь попробуйте с помощью наложения сравнить углы данных треугольников. Угол А с углом А₁, угол В с углом В₁, угол С с углом С₁. Как вы заметили, эти углы соответственно равны. Запишите определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Даны треугольники ABC и DEF. Если известно, что AB:DE=BC:EF=AC:DF=k и ∢A=∢D;∢B=∢E;∢C=∢F, то можно сделать вывод, что ΔABC∼ΔDEF. 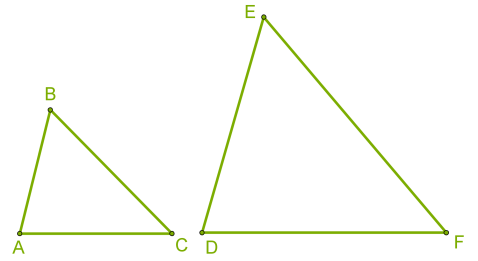При записи подобия треугольников важно соблюдать порядок букв. Равным углам соответствуют определённые буквы, т.е. в этом случае стороны AB и DE, BC и EF,AC и DF называются сходственными Определение. Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.	Измеряют отрезки и записывают отношения. Отвечают: Эти отношения равны. Записывают тему урока. Строят отрезки. Отвечают: 6:4, 9:6 и т.д. Записывают определение. Сравнивают треугольники и делают выводы. Записывают определение.
Первичное закрепление
А теперь выполним с вами упражнения. Задание представлено на слайде. №533 Найдите отношение отрезков АВ и СD, если их длины равны соответственно 15 см. и 20 см. Изменится ли это отношение, если длины отрезков выразить в миллиметрах? Следующее наше задание представлено на слайде. Треугольник АВС подобен треугольнику А₁В₁С₁. Найти x, y, z. №541	Решение:

Постановка домашнего задания
Итак, запишите домашнее задание: прочитать п.56, 57. Выполнить №534, №542, №535 (нужно разобраться в доказательстве).	Записывают домашнее задание в дневники.
Подведение итогов урока
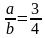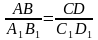Ребята, сегодня вы познакомились с темой «Пропорциональные отрезки. Определение подобных треугольников». Сформулируйте определение подобных треугольников. Верно, спасибо. Что такое коэффициент подобия? Все верно, молодцы. На этом наш урок закончен. Спасибо за урок. До свидания!	Отвечают: Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого. Отвечают: Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.