Разработка конспекта урока: Урок изучения нового
«Формула разности квадратов»
Учебник: 7 класс: учеб. для общеобразовательных учреждений/ [Г.В.Дорофеев, С.Б. Суворова, Е.А.Бунимович и д.р.] – 5-е изд. – М.: Просвещение, 2017. – 287 с. Глава VIII «Разложение многочленов на множители», §4 – Формула разности квадратов.
Тип урока: урок изучения нового
Учебная задача: В совместной деятельности с учащимися вывести формулу разности квадратов и выявить виды задач, решаемых на основе этой формулы
Цели урока:
Образовательные: организовать деятельность учащихся, направленную на самостоятельный вывод формулы разности квадратов; выработать умение распознавать формулу разности квадратов в различных ситуациях, выделять эту формулу среди других выражений, применять ее при преобразовании выражений.
Развивающие: развивать у учащихся математическую речь, способствовать развитию самостоятельности.
Воспитательные: воспитывать интерес к математике, дисциплинированность, ответственное отношение к учебному труду
Методы обучения: частично-поисковые, репродуктивный метод.
Форма работы: фронтальная.
Средства обучения: традиционные, презентация.
Структура урока:
| № | Этап урока | Хронометраж |
| 1 | Мотивация к учебной деятельности | 2мин |
| 2 | Актуализация и фиксирование индивидуального затруднения в пробном учебном действии | 7мин |
| 3 | Открытие нового знания (построение проекта выхода из затруднения) Физкультминутка | 14мин
1мин
|
| 4 | Первичное закрепление . Включение нового знания в систему знаний, повторение и контроль | 18мин |
| 5 | Рефлексия учебной деятельности на уроке. Итог урока | 2мин |
| 6 | Информация о домашнем задании | 1мин |
Оборудование: компьютер, мультимедийный проектор
| Деятельность учителя | Деятельность учеников |
| Мотивация к учебной деятельности |
| Звонок прозвенел. Он напомнил нам с вами, Что время открытий пришло. Я рада увидеть всех в этом классе. Мы начинаем урок. Проверьте наличие на партах тетрадей, учебников
| Приветствуют учителя. Проверяют наличие на партах тетрадей, учебников
|
| Актуализация и фиксирование индивидуального затруднения в пробном учебном действии |
|
Идёт фронтальная устная работа, учитель ведёт беседу с учениками.
|
| Одночлен | 8 | 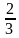
| 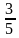 b b
| 0,7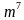 | | Квадрат одночлена | 64 | 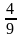
| 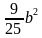
| 0,49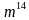 |
Записать в виде алгебраического выражения: а) разность чисел m и n б) разность квадратов чисел m и n в) сумму квадратов чисел m и n | Заполняют таблицу
Записывают ответы: а) m - n б)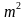 - - 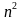 в)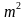 + + 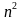 |
-
Снегурочке надо купить к Новому году 87 подарков по цене 93 рубля. Сколько рублей будет стоить вся покупка? Кто может быстро дать ответ? -
Найдите площадь земельного участка Деда Мороза. 
| Ученики правильно составляют выражения 87*93 и 108*108-8*8, но быстро вычислить не могут.
|
| Выполните умножение и приведите подобные члены: -
(m – n)(m + n) -
(c - 0,4)( c + 0,4) -
(6c – 5b )( 6c + 5b) -
(7 - 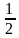 x) (7 + x) (7 + 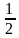 x) x) -
( a – b)( a + b) Что заметили при умножении разности чисел на их сумму? Сделайте вывод | Ученики отвечают: 1 )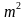 - - 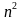 2) 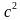 - 0,16 - 0,16 3) 36 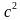 - 25 - 25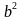 4) 49 b - -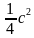 5)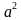 - - 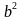
В результате получается разность их квадратов |
| Деятельность учителя | Деятельность учеников |
| Открытие нового знания (построение проекта выхода из затруднения) |
| Итак, мы умножили сумму двух чисел на их разность и получили: (a+b)(a-b) = a2-b2.
Полученную формулу: (a+b)(a-b) = a2-b2 или a2-b2 = (a+b)(a-b) называют формулой разности квадратов и читается она так: 1) Произведение разности и суммы двух чисел равно разности квадратов этих чисел. Т.к. с помощью этой формулы можно в дальнейшем быстро умножать сумму и разность двух чисел, то она относиться к формулам сокращённого умножения. 2)Разность квадратов двух чисел равна произведению разности и суммы этих чисел.
Рассмотрим, какие примеры решаются на основе данной формулы:
Вычислите , применяя формулы сокращенного умножения
а) 52 * 48 б) 104 * 96
Выполните умножение: а) (3с – b) (3c+b)  б) ( б) ( 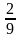 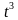 - - 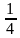  ) ) ( ( 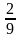 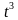 + + 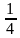  ) )
в) ( 0,1m – 8)(0,1 +8) г) ( 6 - 0, 5 - 0, 5  ) ( 6 ) ( 6 + 0, 5 + 0, 5  ) ) | - прочитайте полученное выражение?
Решение:
а) 52 * 48= (50+2)(50-2)=  - - = 2500-4=2496 = 2500-4=2496 б) 104 * 96 = (100 – 4) ( 100 +4) =  - -  = = 10000-16 = 9984
Решение: а ) … = ( - - 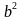 = =  - - 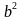 б ) … =  – –  = = – –  в) … =  - -  = =  - 64 - 64 г) … =   = =  – – 
Чтобы разложить двучлен на множители на основе формулы разности квадратов, нужно выделить квадрат первого числа, квадрат второго числа, проверить стоит ли между ними знак «-» и воспользоваться формулой.
Не можем разложить на множители с помощью формулы разности квадратов.
|
| Физкультминутка |
|
-
Реснички опускаются… -
Глазки закрываются… -
Мы спокойно отдыхаем… (два раза). -
Сном волшебным засыпаем… -
Дышатся легко… ровно… глубоко… -
Наши руки отдыхают… -
Отдыхают, засыпают… (два раза). -
Шея не напряжена… -
Губы чуть приоткрываются… -
Всё чудесно расслабляется… (два раза). Дышится легко… ровно… глубоко
| Учащиеся выполняют упражнение |
| Первичное закрепление . Включение нового знания в систему знаний, повторение и контроль |
| Самостоятельная работа ( обучающая) Вариант 1 1. а2-49 2. 0,04х2 -9 3.(8-m)(8+m) 4.(2у-1)(2у+1) Вариант 2 1. а2-64 2. 0,36х2 -25 3.(10-m)(10+m) 4.(3у-1)(3у+1)
| Решение : Вариант 1 1. а2-49 = (a -7)(a +7) 2. 0,04х2 -9 = (0,2x – 3 )( 0,2 x+ 3) 3.(8-m)(8+m) = 64 - 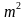 4.(2у-1)(2у+1)=  - 1 - 1 Вариант 2 1. а2-64 = (a -8)( a +8) 2. 0,36х2 -25= ( 0,6 x – 5)( 0,6x +5) 3.(10-m)(10+m) = 100 - 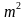 4.(3у-1)(3у+1) =  -1 -1
|
|
| Учащиеся выполняют в тетради и один у доски |
|
Вычисли( самостоятельно по уровням) 1 уровень: 19 * 21 ; 28 * 32 ; 37 * 43 2 уровень: 198* 202 ; 301 * 299 ; 396 * 404 3 уровень: 997 * 1003 ; 1999 * 2001 ; 40003 * 39997 |
Учащиеся решают , затем выполняют самопроверку |
|
Решить уравнение: 1) x2 - 4(5 – x) = (x – 2)(x + 2);
2) (3x + 4)(4 – 3x) = 43 – 9(x + 1)(x - 5).
| Решение: -
x2- 20 + 4x = x2 – 4, x2 + 4x - x2 = – 4 + 20, 4х = 16, х = 4 Ответ: 4 -
16 – 9x2 = 43 – 9x2 - 9x + 45x + 45, – 9x2 + 9x2 + 9x - 45x = 43 + 45 – 16, - 36 х = 72, х = -2 Ответ: - 2 |
|
Найдите выражения, к которым можно применить формулу разности квадратов или формулу сокращенного умножения 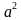 - - 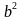 = ( a –b)( a + b) ; = ( a –b)( a + b) ;
( a –b)( a + b) = 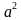 - - 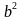
  - -  ; б) ; б) 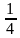  - -  ; в) ; в) 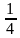  + +  ; ; г) ( x +3)(x -3) ; д) ( 8+ m)(8-m) ; е) 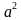 - 4а - 4а | Ответ: а ; г ; д |
| Рефлексия учебной деятельности на уроке. Итог урока |
| - какова была цель урока?
- достигли ли мы её?
-как мы её достигли? Какие примеры решали на основе этой формулы?
| учится пользоваться формулой разности квадратов для разложения многочлена на множители и решения других задач. - Да.
-Решали задания и примеры, где нужно было разложить многочлен на множители, при этом пользовались формулой разности квадратов. Также вычисляли с помощью этой формулы сложные числовые примеры. Решали алгебраические уравнения. |
|
Информация о домашнем задании
|
| П. 8.3 № 857(б,г,е), 858(б, г ) ; 863(б, г , е) | Записывают домашнее задание в дневники |






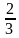
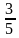 b
b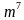
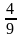
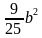
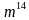
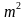 -
- 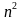

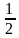 x) (7 +
x) (7 + 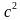 - 0,16
- 0,16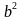
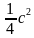
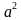 -
-  б) (
б) ( 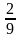
 -
-