| Организационный этап
На уроках математики вы знакомились с решением различных алгебраических уравнений и их систем. Более экзотические – логические уравнения, в которых все величины могут принимать только два значения: «истина (1)» или «ложь (0)». Традиционно эти уравнения тоже относятся к математике, но на практике логические уравнения и их системы оказались полезны при разработке цифровых логических устройств, поэтому в ЕГЭ по информатике появились задания, в которых необходимо решить логическое уравнение или определить количество решений логического уравнения. Откроем тетради, запишем тему нашего сегодняшнего урока: «Решение логических уравнений» Итак, как вы думаете, какая задача стоит перед нами на сегодняшнем уроке?
Правильно, наша сегодняшняя задача – научиться определять количество решений логического уравнения.
Актуализация знаний Какие формы мышления вы знаете? Что такое высказывание?
Какой логической операции соответствуют следующие таблицы истинности? | A | B | F | | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 1 |
| A | B | F | | 0 | 0 | 0 | | 0 | 1 | 0 | | 1 | 0 | 0 | | 1 | 1 | 1 |
| A | B | F | | 0 | 0 | 1 | | 0 | 1 | 1 | | 1 | 0 | 0 | | 1 | 1 | 1 |
| A | B | F | | 0 | 0 | 0 | | 0 | 1 | 1 | | 1 | 0 | 1 | | 1 | 1 | 0 |
Открытие нового знания
Существуют различные способы решения логических уравнений. На сегодняшнем уроке мы рассмотрим три из них. -
Сколько различных решений имеет логическое уравнение? J^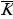 ^L^ ^L^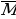 ^(N˅ ^(N˅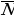 ) = 0 ) = 0 Как вы думаете, что является решением данного уравнения?
Верно. Запишем, что решением логического уравнения является такой набор аргументов, который удовлетворяет уравнению. В нашем примере 5 логических аргументов, каждый аргумент принимает значение либо «0», либо «1». Следовательно, количество таких наборов 25=32. Пойдем методом от противного. Определим, сколько решений имеет обратное уравнение. Вычтем их из общего количества решений и получим искомый ответ. Попробуем упростить наше уравнение. Ребята, как можно это сделать? Верно, а конъюнкция любого логического выражения и 1 дает само это выражение. То есть исходное выражение упростится. Запишем его: J^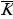 ^L^ ^L^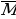 = 0. = 0. Перепишем обратное уравнение, решением которого и займемся. J^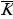 ^L^ ^L^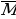 = 1.(*) Обозначим его *. = 1.(*) Обозначим его *. Как мы видим, между аргументами стоит операция конъюнкции. В каких случаях конъюнкция принимает значение ИСТИНА? То есть, уравнению (*) удовлетворяет следующий набор аргументов: J=1 K=0 L=1 M=0 Значение пятого аргумента N безразлично. Поэтому к данному набору мы должны добавить N=0 и N=1. | J | 1 | 1 | | K | 0 | 0 | | L | 1 | 1 | | M | 0 | 0 | | N | 0 | 1 |
Таким образом, у нас получается 2 набора значений, удовлетворяющих уравнению (*). Следовательно, оставшиеся наборы значений являются решениями исходного уравнения. 32-2=30. Ответ: 30 решений. Это и есть ответ к нашему заданию. Мы использовали метод от противного (исключение неподходящего решения или решение обратной задачи). Способ выбран правильно, поэтому решение задачи оказалось простым и понятным. Решим следующую задачу. -
Сколько различных решений имеет уравнение? ((K^L^M) → (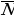 → P))^(( → P))^((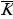 ˅ ˅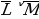 ) → (N˅P)) = 1. ) → (N˅P)) = 1. Для начала рассмотрим структуру уравнения. Что мы здесь видим? (…)^(…)=1.
В каком случае конъюнкция истина?
Что еще мы можем увидеть? (→)^(→)=1.
Вспомним, в каком случае импликация ложна?
Верно, то есть, дальше мы должны рассматривать 9 вариантов решения, что усложняет задачу. Поэтому, мы пойдем другим путем. Попробуем упростить исходное выражение. Обозначим цифрами выражения в скобках. 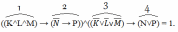 Заметим, что выражения 1 и 3 имеют общее, так же как 2 и 4. Попробуем их упростить. Итак, выражение 2 можно заменить через базовые логические операции. Что это за формула? Верно. Это будет выглядеть следующим образом: 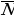 → P = N˅P → P = N˅P Итак, что мы можем заметить?
Рассмотрим теперь выражение 1, чтобы изменить это логическое выражение, попробуем выполнить отрицание: (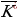 ). По закону де Моргана, разорвем отрицание и запишем в новом виде: ). По закону де Моргана, разорвем отрицание и запишем в новом виде: (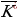 ) = ) = 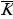 ˅ ˅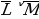 . . Получили, что выражение 1 обратно выражению 3. Итак, напрашивается способ замены переменной. Введем новые переменные: N˅P=a K^L^M=b. Запишем исходное уравнение в новых переменных. (b→a)^(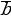 →a)=1. →a)=1. Упрощаем выражение. Запишем импликацию, через базовые логические операции. (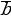 ˅a)^(b˅a)=1. ˅a)^(b˅a)=1. Каким образом мы можем упростить полученное выражение?
Если нет, то мы легко можем это доказать. (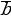 ˅a)^(b˅a) = ( ˅a)^(b˅a) = (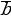 ^b)˅(a^b)˅(a^ ^b)˅(a^b)˅(a^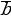 ) ˅(a^a)=a^b˅a^ ) ˅(a^a)=a^b˅a^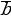 ˅a=a^(b˅ ˅a=a^(b˅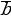 ˅1)= ˅1)= a^1=a=1. Вернемся к исходным переменным и запишем тождественное уравнение. N˅P=1(*). K, L, M – любые, так как в записи уравнения они не участвуют. Дизъюнкция истина, когда хотя бы один из ее аргументов имел значение истина. Выписываем пары подходящих значений для N и P. | N= | 1 | P= | 1 | | N= | 0 | P= | 1 | | N= | 1 | P= | 0 |
Каждую пару подходящих значений мы должны дописать значениями K, L, M. Значения K, L, M –любые, всего таких комбинаций 23=8. Чтобы построить полные наборы, запишем таблицу истинности. Переберем в ней все возможные наборы аргументов K, L, M.
| K | L | M | N | P | | 0 | 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 1 | 1 | | 0 | 1 | 0 | 1 | 1 | | 0 | 1 | 1 | 1 | 1 | | 1 | 0 | 0 | 1 | 1 | | 1 | 0 | 1 | 1 | 1 | | 1 | 1 | 0 | 1 | 1 | | 1 | 1 | 1 | 1 | 1 |
Дописать каждый набор мы должны подходящими значениями N и P. В первом случаем N и P всегда 1. Таким образом получаем 8 различных наборов значений аргументов, каждый из которых удовлетворяет исходному уравнению. То есть, мы имеем 8 решений. Для второй пары подходящих N и P мы получаем еще 8 решений и аналогично для третьей пары. Таким образом, общее число решений будет равно: 8+8+8=24. Ответ: 24 решения. Всего 24 подходящих наборов аргументов или 24 решения уравнения. -
Сколько различных решений имеет уравнение? ((J→K)→(M^N))^((J^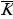 )→( )→(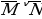 ))^ ))^ (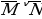 ˅K˅L)=1. ˅K˅L)=1.
Начнем с анализ его структуры. Мы видим, что конъюнкция трех аргументов тождественно равна 1. Это равенство выполняется только в одном случае, в каком?
Перейдем от уравнения к системе более простых уравнений. Перепишем их: 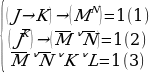 Зададимся вопросом, а нужны ли нам здесь круглые скобки? Действительно, зная приоритет операций, отвечаем, что нет. Но структуру уравнения лучше видно, если эти скобки есть. Вот она, система трех, более простых уравнений. Пронумеруем эти равнения. Итак, решением системы уравнений будет такое решение, которое одновременно удовлетворяет всем трем логическим уравнениям. Начнем с уравнения (1). Перепишем его отдельной строкой и сразу упростим. Первую импликацию записываем через базовые логические операции, сразу разворачиваем вторую импликацию по тому же правилу, далее по закону де Моргана разрываем отрицание над дизъюнкцией и получаем окончательный вид уравнения: (J→K)→(M^N)=J^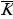 ˅M^N=1. ˅M^N=1. Найдем количество решений этого уравнения через систему более простых уравнений. Выпишем эти уравнения. Итак, дизъюнкция истина, когда хотя бы один из ее аргументов имеет значение истина. То есть 3 варианта, удовлетворяющих уравнению мы и выпишем: 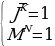 (*) (*) 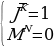 (**) (**) 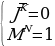 (***) (***) Мы получили совсем простые уравнения, поэтому воспользуемся таблицей истинности и порассуждаем. Мы переходим от решения уравнения (1) к системе уравнений, но в отличие от первой системы, они объединены между собой логической операцией ИЛИ. Это значит, что любое решение любой их трех систем удовлетворяет уравнению (1). Обозначим это специальным алгебраическим значком – квадратная скобочка. Рассмотрим систему (*): | J | K | L | M | N | | 1 | 0 | 0 | 1 | 1 | | 1 | 0 | 1 | 1 | 1 | | 1 | 0 | 0 | 0 | 0 | | 1 | 0 | 1 | 0 | 0 | | 1 | 0 | 0 | 0 | 1 | | 1 | 0 | 1 | 0 | 1 | | 1 | 0 | 0 | 1 | 0 | | 1 | 0 | 1 | 1 | 0 | | 0 | 0 | 0 | 1 | 1 | | 0 | 0 | 1 | 1 | 1 | | 0 | 1 | 0 | 1 | 1 | | 0 | 1 | 1 | 1 | 1 | | 1 | 1 | 0 | 1 | 1 | | 1 | 1 | 1 | 1 | 1 |
Конъюнкция истина только в одном случае, когда все ее аргументы имеют значение истина. От аргумента L система не зависит, поэтому мы должны дописать в этот набор все возможные значения L. Таким образом, система (*) дает нам 2 решения. Занесем данные в таблицу. Первое уравнение системы (**) требует истинности J и ложности K, а вот второе уравнение удовлетворяется тремя наборами M и N. Также каждый из этих наборов мы должны дописать всеми возможными значениями L. Таким образом, система (**) дает нам 6 решений. Запишем полностью эти наборы, так как нам придется их анализировать. Система (***) требует, что бы M и N были истинны, первому уравнению удовлетворяет 3 пары значений, таким образом, мы получаем 3 набора значений J, K, M, N и должны дополнить эти наборы всеми возможными значениями L. Таким образом, система (***) даст нам еще 6 решений. Итак, уравнение (1) исходной системы имеет 14 решений. Вернемся к исходной системе уравнений и запишем: уравнение (1) имеет 14 решений. Теперь мы должны убедиться, что все эти 14 решений удовлетворяют уравнениям (2) и (3). Решаем уравнение (2): 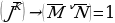
Получаем два решения, которые не удовлетворяют уравнению (2). И мы должны их вычеркнуть из таблицы решений первого уравнения, если они там есть. Посмотрев внимательно таблицу, мы видим, что оба эти набора есть в таблице, и мы должны их вычеркнуть. Итак, из 14 решений осталось 12. Приступим к уравнению (3): 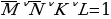
Внимательно рассмотрим таблицу решений первого уравнения и вычеркнем получившиеся наборы. Заметим, что второго набора в нашей таблице нет. Итак, из 14 решений, которые дало нам уравнение (1) мы вычеркнули 2 решения, не удовлетворяющие уравнению (2) и одно решение, не удовлетворяющее уравнению (3). Задача решена. Ответ: 11 решений. Этот метод решения логического уравнения можно назвать сведение уравнения к системе более простых уравнений. Мы воспользовались этим методом дважды. Решение оказалось не сложным, хоть и несколько затянутым.
Закрепление нового материала Итак, на сегодняшнем уроке мы с вами решили 3 логических уравнения тремя разными способами. Кто может назвать эти способы?
Верно. В чем заключалась суть каждого из способов?
Какой вывод мы можем сделать из проделанной сегодня работы?
Подведение итогов урока
Надеюсь, наш сегодняшний урок прошел познавательно и вы узнали много нового для себя. Помните, что правильно выбранный метод делает решение совсем не сложным. Запишите домашнее задание: Сколько решений имеют следующие уравнения: -
(A→B)˅C˅(D^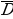 )=1. )=1. -
( )˅ )˅ ( )˅(M^J)=0. )˅(M^J)=0.
|
Внимательно слушают учителя, по необходимости отвечают на вопросы
Научиться решать логические уравнения, научиться определять количество решений логического уравнения
Понятие, высказывание, умозаключение Высказывание – повествовательное выражение, которое может принимать одно из двух значений: «истинна» или «ложь»
Дизъюнкция, логическое сложение
Конъюнкция, логическое умножение
Импликация, логическое следование
Исключающее ИЛИ, сложение по модулю 2
Все возможные J, K, L, M, N при которых будет выполнено равенство.
Выражение в скобочках (N˅¬N)=1
Конъюнкция истина, если все аргументы имеют значение истина
Конъюнкция двух логических выражений тождественно равна истине. Конъюнкция истина, когда все аргументы имеют значение истина. Слева и справа присутствует импликация. Импликация ложна, если первый аргумент истина, а второй –ложь.
Формула замены импликации дизъюнкцией
Выражение 2 тождественно выражению 4.
Слева можно увидеть формулу.
Когда все 3 аргумента равны 1.
Нет
Решение: 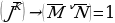 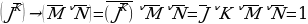 Решать это уравнение удобно методом от противного, как в первой задаче. (¬J)˅K˅(¬M)˅(¬N)=0. Дизъюнкция ложна, когда все аргументы ложны, то есть, значение J=1; K=0; M=1; N=1. Так как от значения L решение уравнения не зависит, мы должны дополнить этот набор всеми возможными значениями L. | J | K | L | M | N | | 1 | 0 | 0 | 1 | 1 | | 1 | 0 | 1 | 1 | 1 |
Решение: 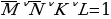 Пойдем методом от противного и найдем те значения аргументов, которые не удовлетворяют уравнению (3). 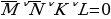 . . Запишем их по порядку. Для J оставим место. Дополним набор значениями J. И получим два набора, которых не должно быть в нашей таблице.
| J | K | L | M | N | | 0 | 0 | 0 | 1 | 1 | | 1 | 0 | 0 | 1 | 1 |
Метод от противного, метод замены переменных, сведение уравнения к системе более простых уравнений Метод от противного заключался в том, что мы вычисляли общее количество решений исходного уравнения, решали обратное уравнение и из общего количества решений вычитали количество решений обратного уравнения; в методе замены переменных мы анализировали структуру уравнения, замечая похожие выражения пытались упростить части исходного уравнения, после упрощения заменяли некоторые его части другими буквами и решали уравнение уже с ними; сведение уравнения к системе более простых уравнений: опять же начинали с анализа исходного уравнения, разбивали его на более простые части и решали по отдельности каждое уравнение полученной системы Не всегда можно решить логическое уравнение только одним способом, необходимо сначала тщательно его проанализировать и выбрать способ его решения |






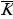 ^L^
^L^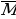 ^(N˅
^(N˅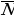 ) = 0
) = 0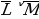 ) → (N˅P)) = 1.
) → (N˅P)) = 1.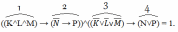
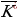 ). По закону де Моргана, разорвем отрицание и запишем в новом виде:
). По закону де Моргана, разорвем отрицание и запишем в новом виде: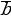 →a)=1.
→a)=1.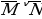 ))^
))^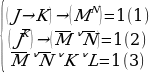
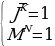 (*)
(*)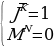 (**)
(**)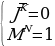 (***)
(***)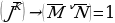
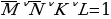
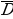 )=1.
)=1. )˅
)˅ )˅(M^J)=0.
)˅(M^J)=0.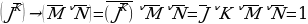
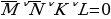 .
.


















